TheSlide.ru

Медианы, биссектрисы и высоты треугольника 7 класс

Содержание

1. Медианы, биссектрисы и высоты треугольника 7 класс
2. медианы треугольника биссектрисы треугольника высоты треугольника
3. Медианой треугольника называется отрезок, соединяющий вершину треугольника
4. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника,
5. Высотой треугольника называется перпендикуляр, проведённый из его
6. Слайд 6
7.  Может ли точка пересечения высот лежать вне треугольника?
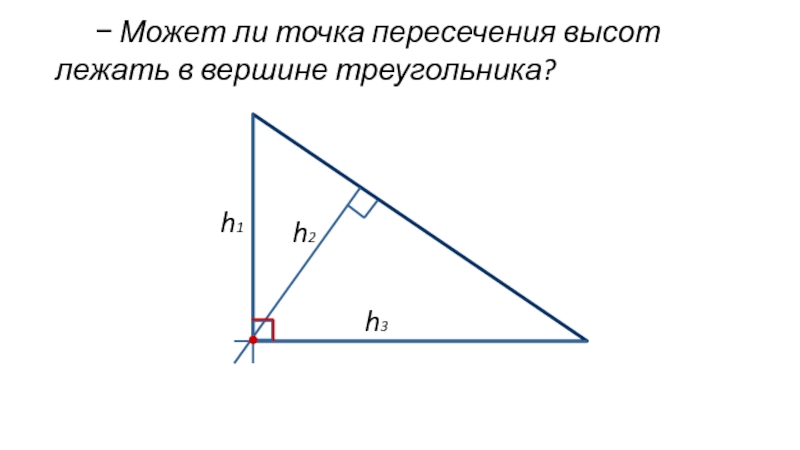
8.  Может ли точка пересечения высот лежать в вершине треугольника?
9. Задача. Отрезок BD – медиана треугольника АВС,
10. Задача. Отрезок AD – медиана треугольника АВС.
11. Скачать презентанцию

медианы треугольника биссектрисы треугольника высоты треугольника

Главная
Геометрия
Медианы, биссектрисы и высоты треугольника 7 класс

Слайды и текст этой презентации

Слайд 1Медианы, биссектрисы и высоты треугольника

Медианы, биссектрисы и высоты треугольника

Слайд 2 медианы треугольника
биссектрисы треугольника
высоты треугольника

медианы треугольника биссектрисы треугольника высоты треугольника

Слайд 3Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей

стороны.
АA1, ВB1 и СC1 – медианы ∆ АВС.
Обозначают:

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. АA1, ВB1 и СC1 – медианы

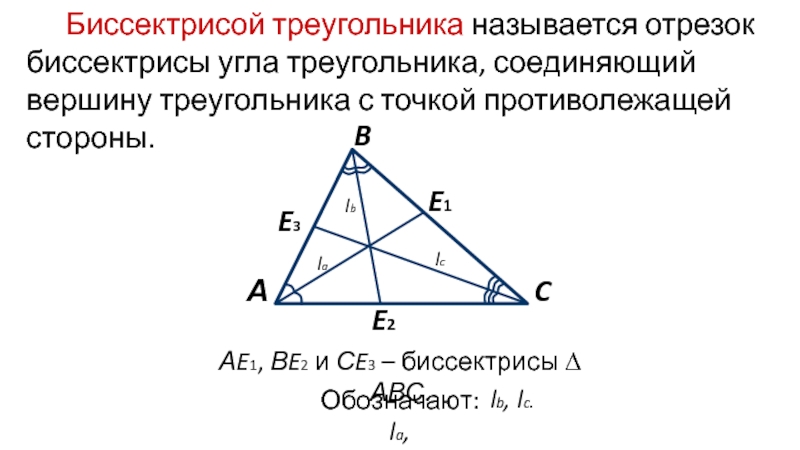
Слайд 4Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника

с точкой противолежащей стороны.
АE1, ВE2 и СE3 – биссектрисы

∆ АВС.

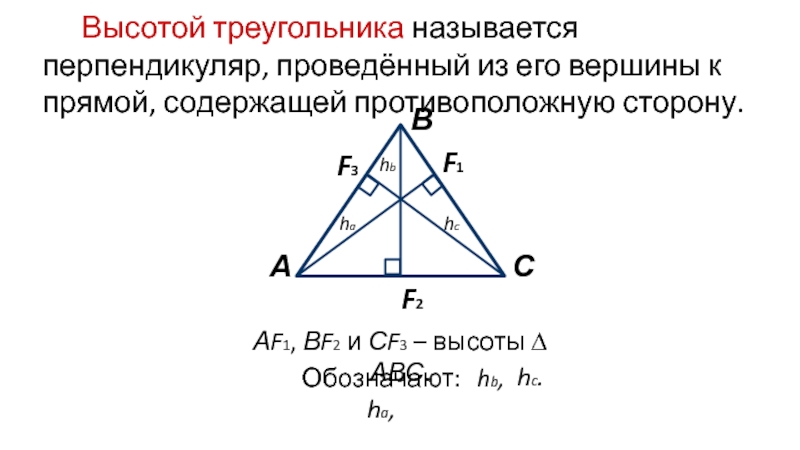
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны. АE1, ВE2 и

Слайд 5Высотой треугольника называется перпендикуляр, проведённый из его вершины к прямой,

содержащей противоположную сторону.
АF1, ВF2 и СF3 – высоты ∆ АВС.

Высотой треугольника называется перпендикуляр, проведённый из его вершины к прямой, содержащей противоположную сторону.АF1, ВF2 и СF3 –

Слайд 6

Слайд 7 Может ли точка пересечения высот лежать вне треугольника?

 Может ли точка пересечения высот лежать вне треугольника?

Слайд 8 Может ли точка пересечения высот лежать в вершине треугольника?

 Может ли точка пересечения высот лежать в вершине треугольника?

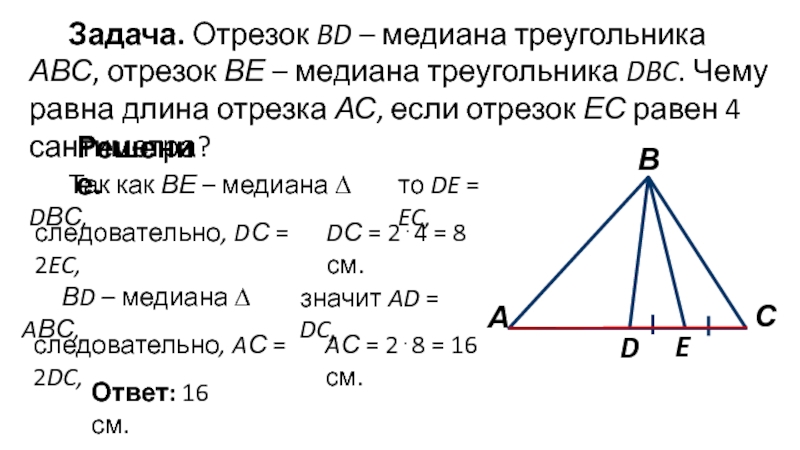
Слайд 9Задача. Отрезок BD – медиана треугольника АВС, отрезок ВЕ –

медиана треугольника DBC. Чему равна длина отрезка АС, если отрезок

ЕС равен 4 сантиметра?

Решение.

Так как ВЕ – медиана ∆ DВС,

то DE = EC,

следовательно, DС = 2EC,

DС = 24 = 8 см.

ВD – медиана ∆ AВС,

значит AD = DC,

следовательно, AС = 2DC,

AС = 28 = 16 см.

Ответ: 16 см.

Задача. Отрезок BD – медиана треугольника АВС, отрезок ВЕ – медиана треугольника DBC. Чему равна длина отрезка

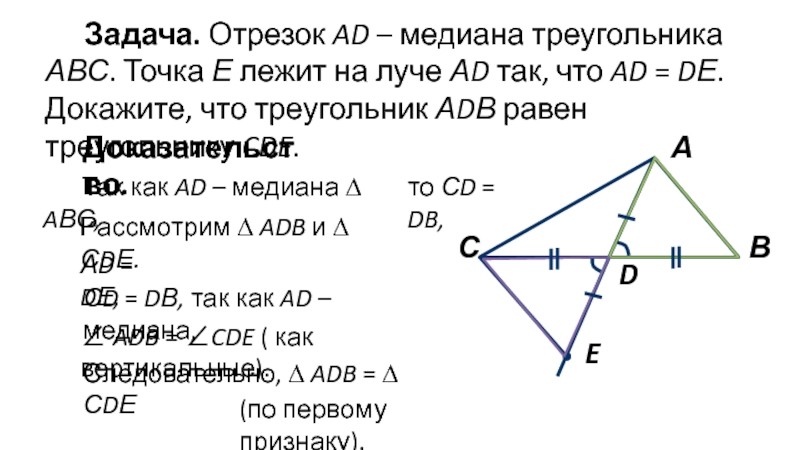
Слайд 10Задача. Отрезок AD – медиана треугольника АВС. Точка Е лежит

на луче АD так, что AD = DЕ. Докажите, что

треугольник АDВ равен треугольнику CDE.

Доказательство.

Так как AD – медиана ∆ AВС,

Рассмотрим ∆ ADB и ∆ СDЕ.

АD = DЕ,

СD = DВ, так как AD – медиана,

Следовательно, ∆ ADB = ∆ СDЕ

(по первому признаку).

Задача. Отрезок AD – медиана треугольника АВС. Точка Е лежит на луче АD так, что AD =

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей