Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неевклидова геометрия
Содержание
- 1. Неевклидова геометрия
- 2. Ученый должен идти по непроторенным путям, несмотря на препятствия.Н.И.Лобачевский
- 3. Цель работы: Провести параллель между геометрией древнегреческого
- 4. Если две прямые образуют с третьей прямой
- 5. И. ЛамбертК. Швейкарт«Трехсторонник» Швейкарта
- 6. Казанский университет1826г, Лобачевский представляет Совету Казанского университета
- 7. В. БуняковскийМ. Остроградский
- 8. ГауссТруды Н.И. Лобачевского
- 9. Слайд 9
- 10. Геометрия Евклида Геометрия ЛобачевскогоСумма внутренних углов треугольникаПодобные треугольники
- 11. Геометрия Евклида Геометрия ЛобачевскогоПризнаки равенства треугольниковРасположение прямых на плоскости
- 12. Теорема о сумме углов четырёхугольникаТеорема. Сумма углов
- 13. Внешний угол треугольникаГеометрия Евклида Геометрия ЛобачевскогоУгол 1
- 14. Задача 1
- 15. Задача 2 Дано: сфера(R;О),
- 16. Заключение В нашей исследовательской работе цель
- 17. Слайд 17
- 18. Спасибо за внимание!
- 19. Скачать презентанцию
Ученый должен идти по непроторенным путям, несмотря на препятствия.Н.И.Лобачевский
Слайды и текст этой презентации
Слайд 1МОУ «Бендерский теоретический лицей»
Выполнили : ученицы 8-Г класса
Костинская Дарья и
Коваджи Анастасия
Слайд 3Цель работы: Провести параллель между геометрией древнегреческого математика Евклида и
русского математика Лобачевского Николая Ивановича.
Гипотеза: Существует ли неевклидова геометрия и
ее отличия от школьнойЗадача : изучить литературу и интернет-ресурсы по
данной теме, рассмотреть различие между
геометрией Евклида и геометрией Лобачевского
Слайд 4Если две прямые образуют с третьей прямой внутренние односторонние углы,
в сумме меньшие двух прямых, то эти прямые пересекаются, причем
с той стороны от третьей прямой, с какой названная сумма углов будет меньше двух прямых углов.
Слайд 6
Казанский университет
1826г, Лобачевский представляет Совету Казанского университета «Сжатое изложение начал
геометрии со строгим доказательством теоремы о параллельных»
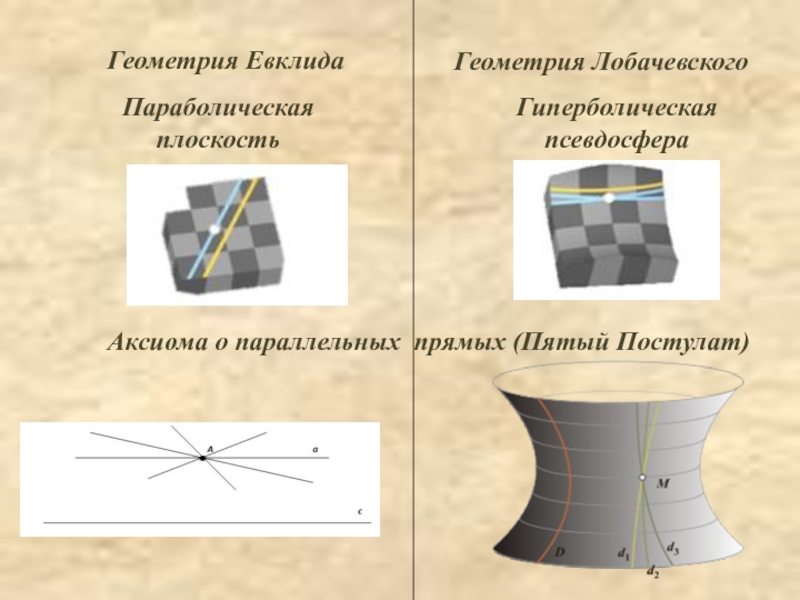
Слайд 9 Геометрия
Евклида
Геометрия Лобачевского
Аксиома о параллельных прямых (Пятый Постулат)
Параболическая
плоскость
Гиперболическая
псевдосфера
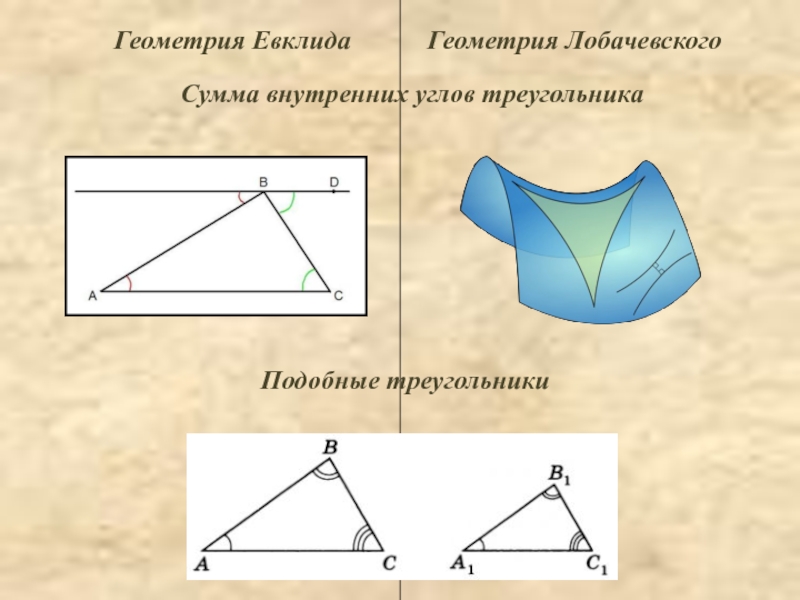
Слайд 10 Геометрия Евклида
Геометрия Лобачевского
Сумма внутренних углов треугольника
Подобные треугольники
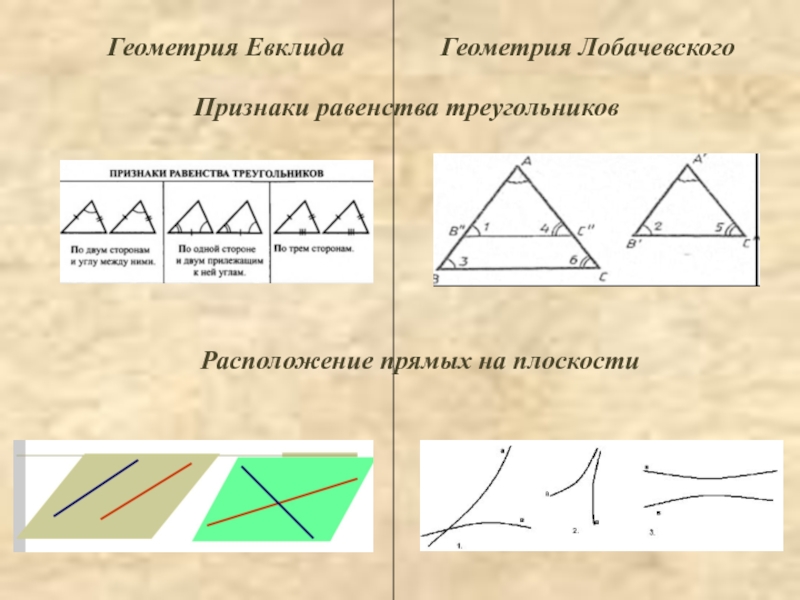
Слайд 11 Геометрия Евклида
Геометрия Лобачевского
Признаки равенства треугольников
Расположение прямых на плоскости
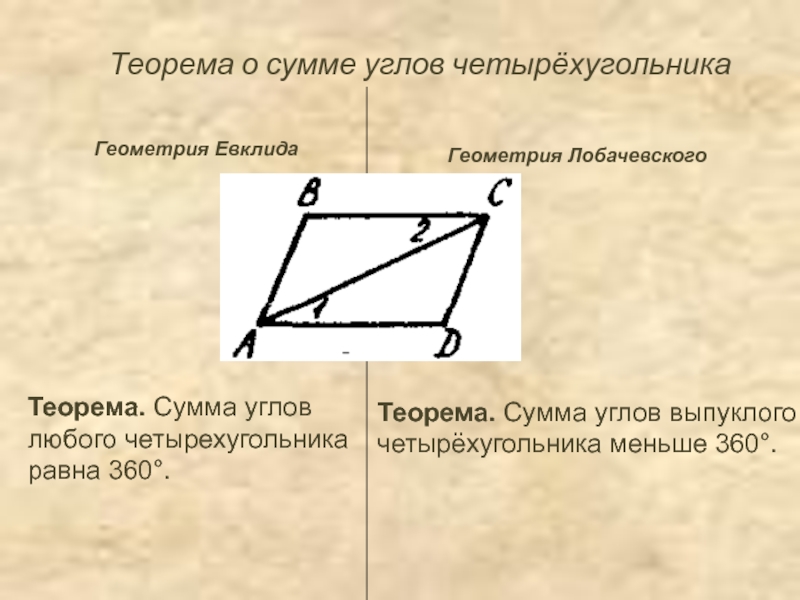
Слайд 12Теорема о сумме углов четырёхугольника
Теорема. Сумма углов
любого четырехугольника
равна
360°.
Теорема. Сумма углов выпуклого
четырёхугольника меньше 360°.
Геометрия Евклида
Геометрия Лобачевского
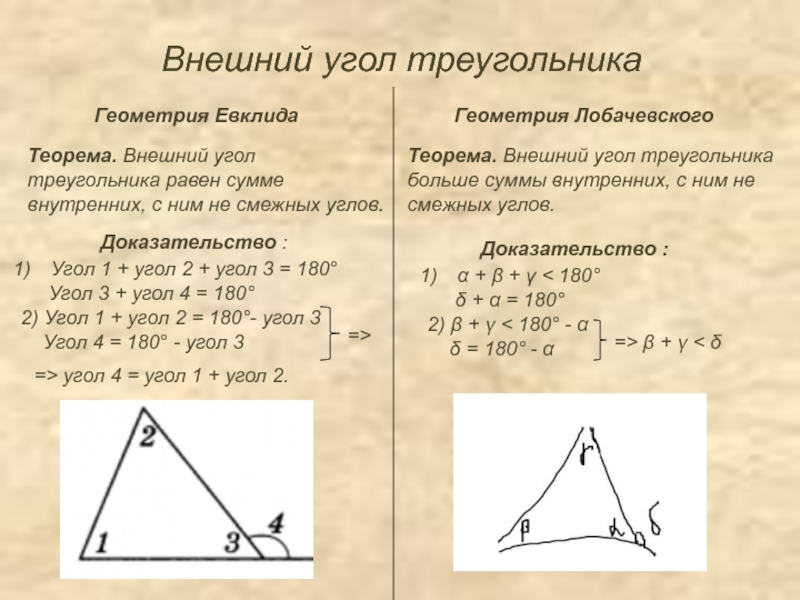
Слайд 13Внешний угол треугольника
Геометрия Евклида
Геометрия Лобачевского
Угол 1 + угол 2
+ угол 3 = 180°
Угол 3 +
угол 4 = 180°2) Угол 1 + угол 2 = 180°- угол 3
Угол 4 = 180° - угол 3
=>
=> угол 4 = угол 1 + угол 2.
α + β + γ < 180°
δ + α = 180°
2) β + γ < 180° - α
δ = 180° - α
=> β + γ < δ
Теорема. Внешний угол
треугольника равен сумме
внутренних, с ним не смежных углов.
Доказательство :
Доказательство :
Теорема. Внешний угол треугольника больше суммы внутренних, с ним не смежных углов.
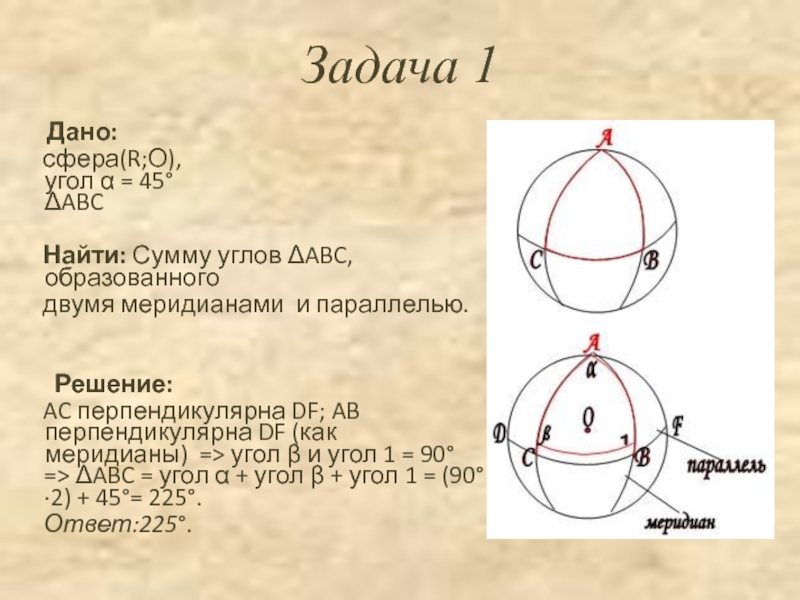
Слайд 14Задача 1
Дано:
сфера(R;О),
угол α = 45°
ΔABC
Найти: Сумму углов ΔABC, образованного двумя меридианами и параллелью.
Решение:
AC перпендикулярна DF; AB перпендикулярна DF (как меридианы) => угол β и угол 1 = 90° => ΔABC = угол α + угол β + угол 1 = (90°·2) + 45°= 225°.
Ответ:225°.
Слайд 15Задача 2
Дано:
сфера(R;О),
две прямые на сфере
Доказать:
любые прямые пересекаются
Доказательство:
Вторая «прямая» полностью лежит в одной из полусфер, потому что первая «прямая» делит сферу
на две половины. Поэтому её радиус (r) < R сферы, т.е.
это не «прямая», а окружность => вторая «прямая» не является прямой => любые две «прямые» пересекаются на сфере, что и требовалось доказать.
Слайд 16Заключение
В нашей исследовательской работе цель была достигнута, так
как были решены все поставленные задачи. В описании данной работы
мы выяснили различия геометрий двух величайших математиков. Содержащиеся в работе сведения дают нам возможность для рассмотрения её в дальнейшем её практического применения. Исследование расширило наши знания о нескольких математиках, а также в корне изменило наше мнение относительно геометрии, изучаемой в школе.
