Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение подобия к доказательству теорем и решению задач
Содержание
- 1. Применение подобия к доказательству теорем и решению задач
- 2. Цели урока:Ввести определение средней линии треугольника.Сформулировать и
- 3. Ход урокаРешение задач по готовым чертежам.Изучение нового материала.Закрепление изученной темы.Итоги урокаДомашнее задание
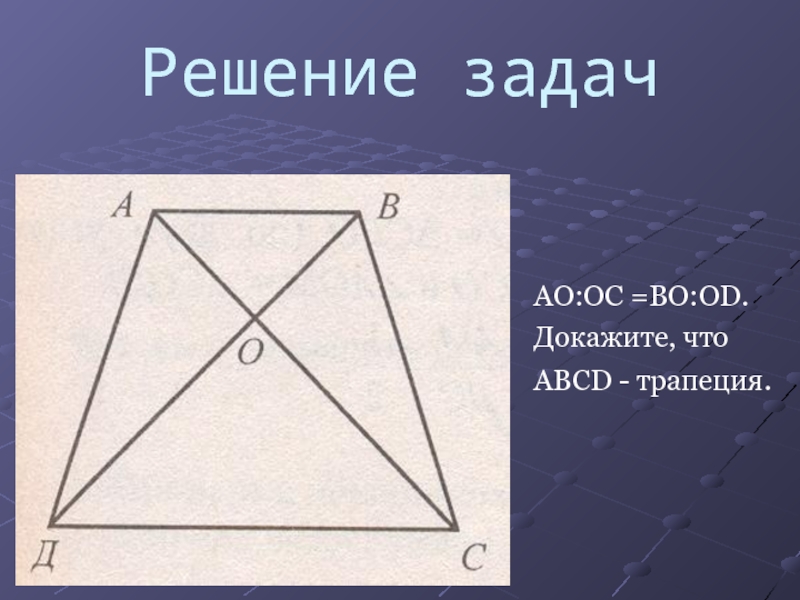
- 4. Решение задачAO:OC =BO:OD.Докажите, чтоABCD - трапеция.
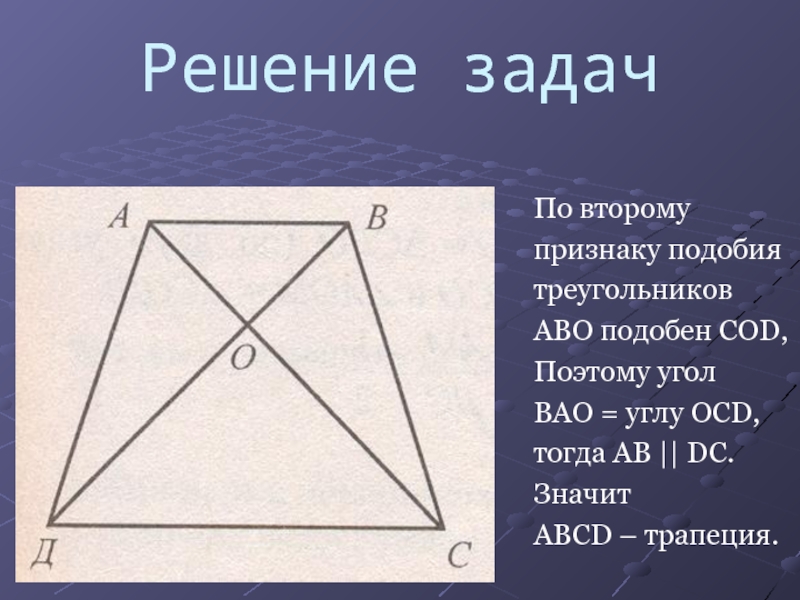
- 5. Решение задачПо второмупризнаку подобиятреугольниковABO подобен COD,Поэтому угол BAO = углу OCD,тогда AB || DС.ЗначитABCD – трапеция.
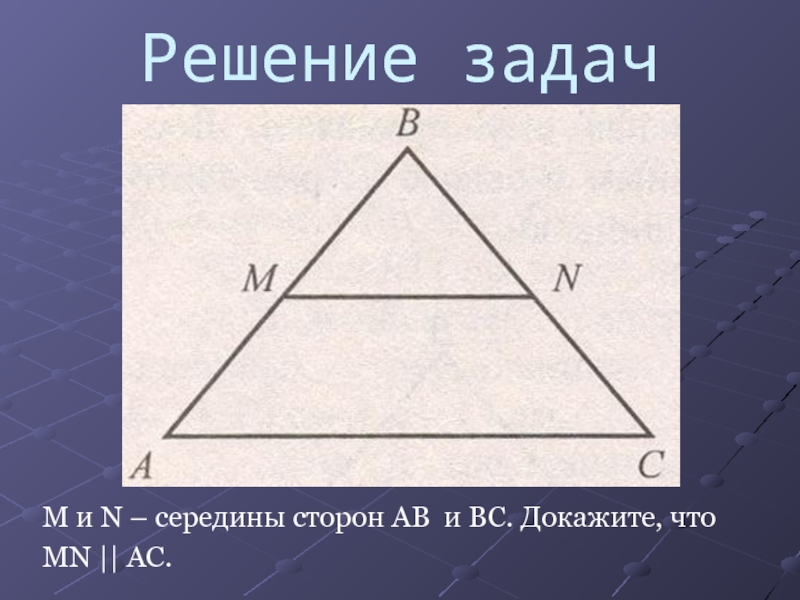
- 6. Решение задачМ и N – середины сторон AB и BC. Докажите, чтоMN || AC.
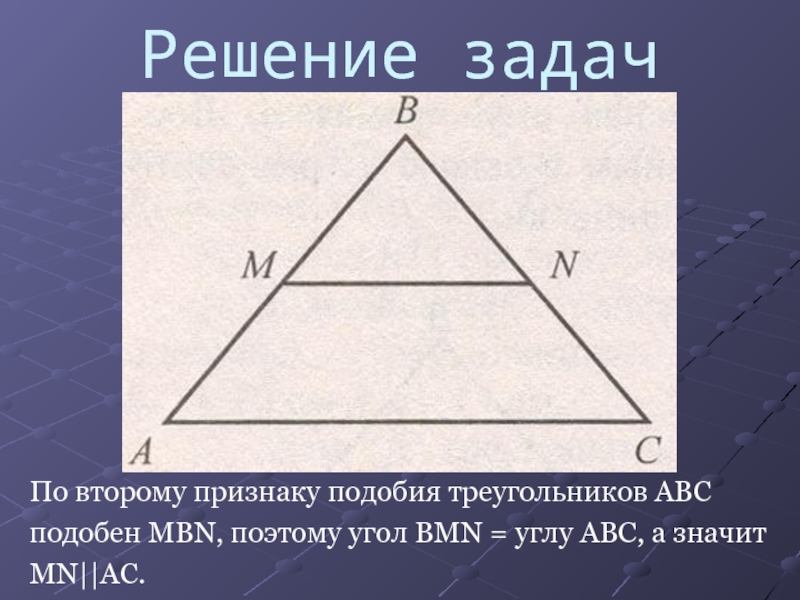
- 7. Решение задачПо второму признаку подобия треугольников ABCподобен MBN, поэтому угол BMN = углу ABC, а значитMN||AC.
- 8. Объяснение нового материалаОпределение средней линии треугольника.Теорема о средней линии треугольника.
- 9. Закрепление изученного материала№ 564 (устно)№ 567№ 1№ 570
- 10. Решение задачи № 567MN – средняя линия
- 11. Решение задачи № 570Треугольник AMO подобен треугольнику
- 12. Итог урокаЕсли AM = MB и MN
- 13. Домашнее заданиеВопросы стр. 154: 8, 9.№ 565№ 566№ 571
- 14. ЛитератураЛ. С. Атанасян и другие «Геометрия»Учебник для
- 15. Скачать презентанцию
Цели урока:Ввести определение средней линии треугольника.Сформулировать и доказать теорему о средней линии треугольника.Рассмотреть решение задач на применение доказанной теоремы.Рассмотреть решение задачи о свойстве медиан треугольника.
Слайды и текст этой презентации
Слайд 2Цели урока:
Ввести определение средней линии треугольника.
Сформулировать и доказать теорему о
средней линии треугольника.
задачи о свойстве медиан треугольника.Слайд 3Ход урока
Решение задач по готовым чертежам.
Изучение нового материала.
Закрепление изученной темы.
Итоги
урока
Домашнее задание
Слайд 5Решение задач
По второму
признаку подобия
треугольников
ABO подобен COD,
Поэтому угол
BAO = углу
OCD,
тогда AB || DС.
Значит
ABCD – трапеция.
Слайд 7Решение задач
По второму признаку подобия треугольников ABC
подобен MBN, поэтому угол
BMN = углу ABC, а значит
MN||AC.
Слайд 8Объяснение нового материала
Определение средней линии треугольника.
Теорема о средней линии треугольника.
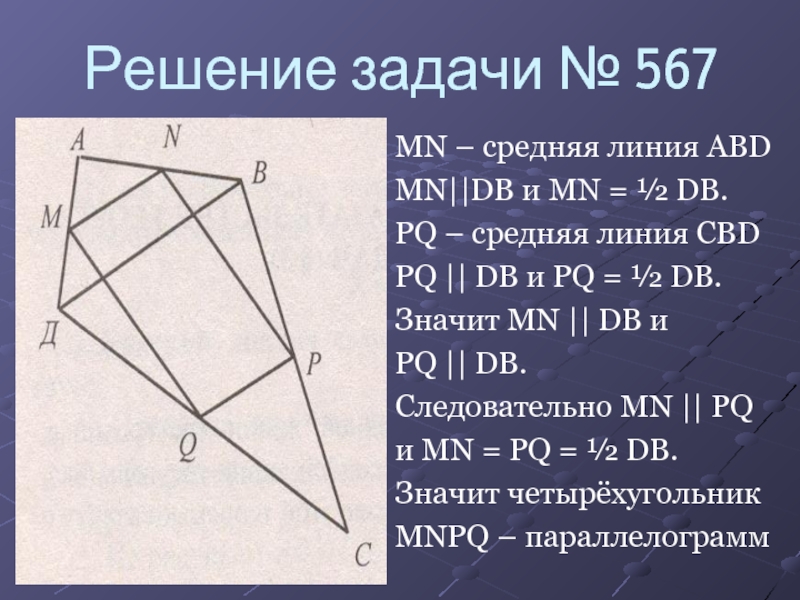
Слайд 10Решение задачи № 567
MN – средняя линия ABD
MN||DB и MN
= ½ DB.
PQ – средняя линия CBD
PQ || DB и
PQ = ½ DB.Значит MN || DB и
PQ || DB.
Следовательно MN || PQ
и MN = PQ = ½ DB.
Значит четырёхугольник
MNPQ – параллелограмм
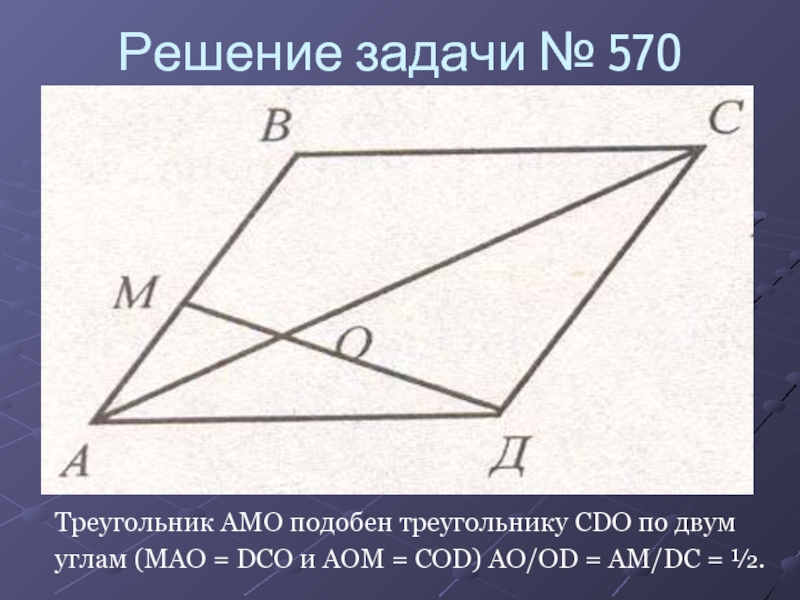
Слайд 11Решение задачи № 570
Треугольник AMO подобен треугольнику CDO по двум
углам
(MAO = DCO и AOM = COD) AO/OD = AM/DC
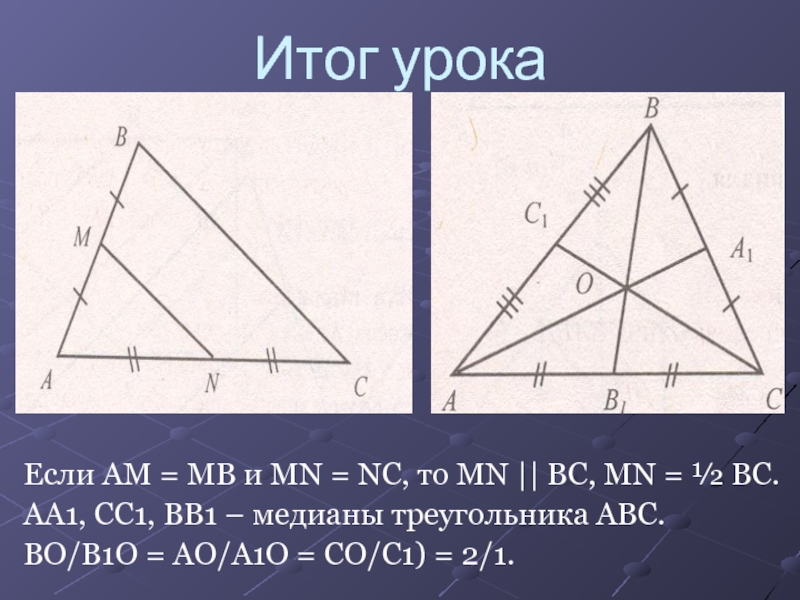
= ½.Слайд 12Итог урока
Если AM = MB и MN = NC, то
MN || BC, MN = ½ BC.
AA1, CC1, BB1 –
медианы треугольника ABC.BO/B1O = AO/A1O = CO/C1) = 2/1.
Слайд 14Литература
Л. С. Атанасян и другие «Геометрия»
Учебник для 7 – 9
классов. Москва просвещение 2002г
Л. С. Атанасян и другие «Геометрия» Пробный
учебник для 6 – 8 классов., Москва просвещение 1981гЛ. С. Атанасян и другие «Изучение геометрии в 7 – 9 классах.
Теги