Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок геометрии " Второй признак равенства треугольников"
Содержание
- 1. Урок геометрии " Второй признак равенства треугольников"
- 2. Первый признак равенства треугольниковЕсли две стороны и
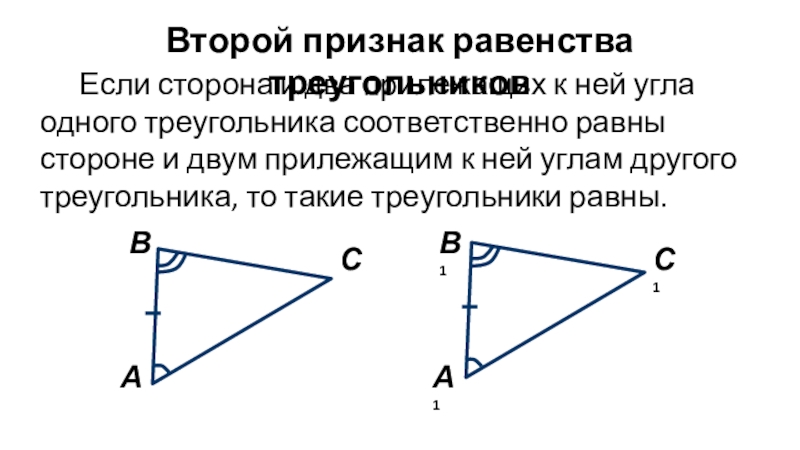
- 3. Второй признак равенства треугольников
- 4. Доказательство. Пусть АВ = А1В1,∠ А =
- 5. Задача. Докажите, что в равнобедренном треугольнике биссектрисы,
- 6. Задача. Точки Е и F лежат соответственно
- 7. Задача. Отрезки АВ и CD пересекаются в
- 8. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Доказательство.
Пусть АВ = А1В1,
∠ А = ∠ А1,
∠ В
= ∠ В1.
Получаем ∆ АВС = ∆ А1В1С1.
Значит, АС =
А1С1,ВС = В1С1.
Теорема доказана.
Слайд 5Задача. Докажите, что в равнобедренном треугольнике биссектрисы, поведённые к боковым
сторонам, равны между собой.
Доказательство.
С
В
А
M
N
∆ АВС – равнобедренный,
АВ = ВС.
АМ,
СN – биссектрисы. Рассмотрим ∆ АМВ и ∆ CNB.
∠ В – общий,
АВ = ВС,
∠ NCB = ∠ MAB.
Тогда ∆ АМВ = ∆ CNB
(по второму признаку).
Следовательно, АМ = СN.
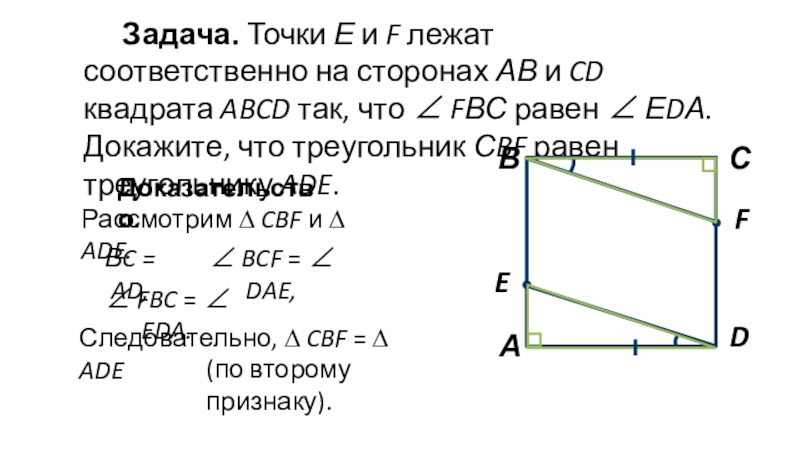
Слайд 6Задача. Точки Е и F лежат соответственно на сторонах АВ
и CD квадрата ABCD так, что ∠ FВС равен ∠
ЕDА. Докажите, что треугольник СBF равен треугольнику ADE.Доказательство.
С
В
А
D
E
F
Рассмотрим ∆ CBF и ∆ ADE.
ВC = AD,
∠ BCF = ∠ DAE,
∠ FBC = ∠ EDA.
Следовательно, ∆ CBF = ∆ ADE
(по второму признаку).
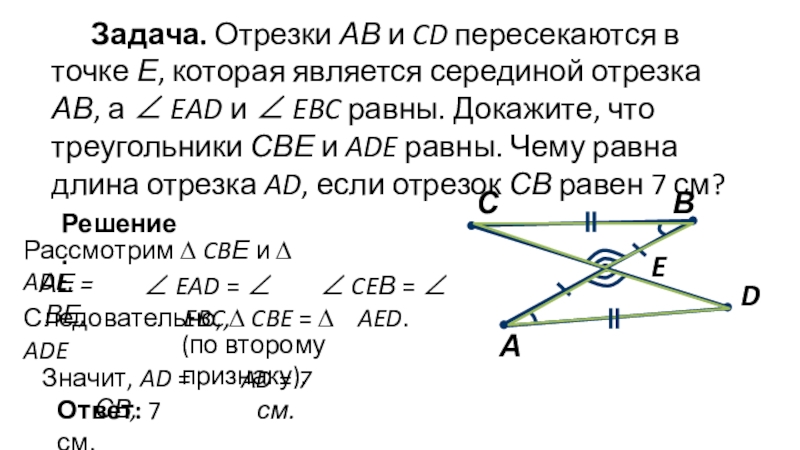
Слайд 7Задача. Отрезки АВ и CD пересекаются в точке Е, которая
является серединой отрезка АВ, а ∠ EAD и ∠ EBC
равны. Докажите, что треугольники СВЕ и ADE равны. Чему равна длина отрезка AD, если отрезок СВ равен 7 см?E
Решение.
Рассмотрим ∆ CBЕ и ∆ ADE.
АЕ = ВЕ,
∠ EAD = ∠ EBC,
∠ CEВ = ∠ AED.
Следовательно, ∆ CBE = ∆ ADE
(по второму признаку).
Значит, AD = СВ,
AD = 7 см.
Ответ: 7 см.