Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площадь треугольника Полезные теоремы, следствия и задачи.
Содержание
- 1. Площадь треугольника Полезные теоремы, следствия и задачи.
- 2. Вспомните ответы на вопросы1) Сформулируй понятие площади
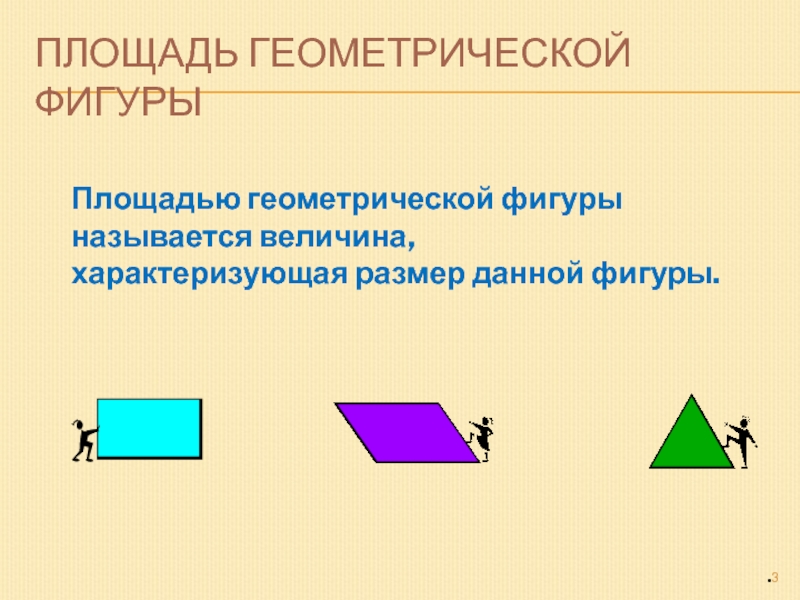
- 3. Площадь геометрической фигурыПлощадью геометрической фигуры называется величина, характеризующая размер данной фигуры.
- 4. Основные свойства площадей геометрических фигур- Любая плоская
- 5. Площадь прямоугольникаПлощадь прямоугольника равна произведению двух его соседних сторон.вS = а · в
- 6. Площадь параллелограммаПлощадь параллелограмма равна произведению его стороны
- 7. Площадь параллелограммаПлощадь параллелограмма равна произведению двух его
- 8. Площадь треугольника ТеоремаПлощадь треугольника равна
- 9. Доказательство теоремыАВДСКS(АВС)= ½ S(АВДС)=1/2 АС · ВК
- 10. Следствия из теоремыПопробуй доказать самостоятельно следующие следствия из теоремы:
- 11. Следствие 1Площадь прямоугольного треугольника равна половине произведения его катетов.АВСS= ½ ВС · АС
- 12. Следствие 2Площадь тупоугольного треугольника равна произведению любой
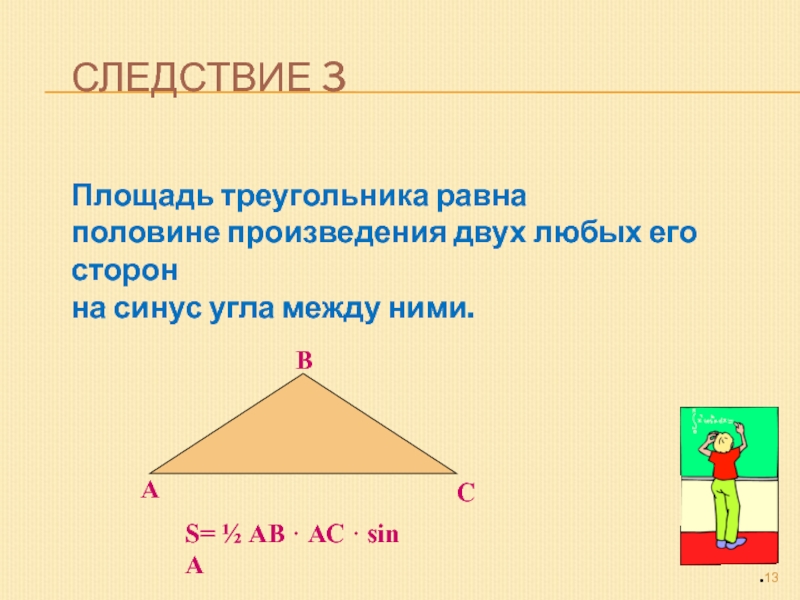
- 13. Следствие 3Площадь треугольника равна половине произведения двух
- 14. Следствие 4Площадь равностороннего треугольника вычисляется по формуле:где а – сторона треугольника
- 15. Сначала реши легкие задачки1. Найти площадь треугольника,
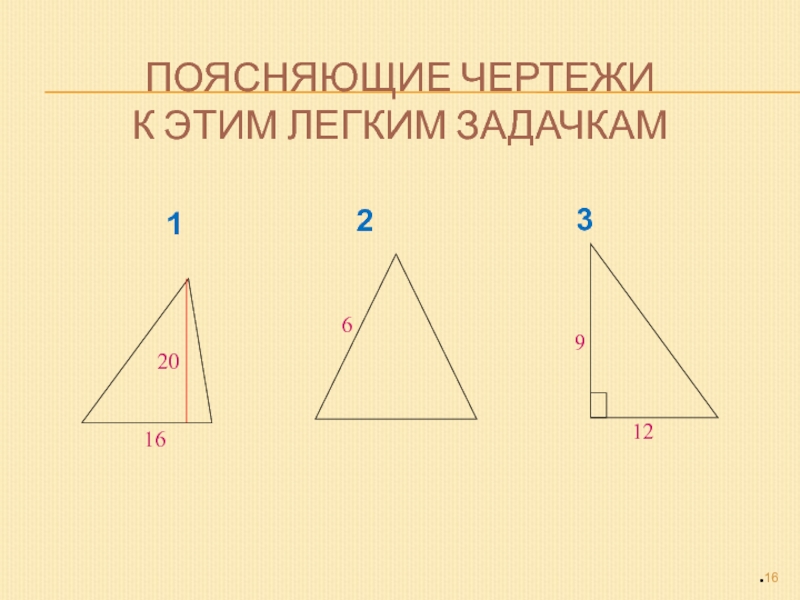
- 16. Поясняющие чертежи к этим легким задачкам123
- 17. Теперь реши задачки потруднее1. В равнобедренном треугольнике
- 18. Теперь реши самые трудные задачи1. Боковая сторона
- 19. Ответы к легким задачкам1. 160 см22. 9 см 23. 54 см 2
- 20. Ответы к более трудным задачкам1. 60 см 22. 3. 24 см 2
- 21. Ответы к самым трудным задачкам1. ½ a2sin22. 3.
- 22. Это интересно! Определение площадей геометрических фигур -
- 23. Например, мы уже
- 24. -Отметим на одной из сторон треугольника точку,
- 25. Поясняющий чертеж
- 26. Исходный треугольник и полученный
- 27. Площадь параллелограмма
- 28. И в заключении…Надеюсь, что эта информация поможет
- 29. Скачать презентанцию
Вспомните ответы на вопросы1) Сформулируй понятие площади геометрической фигуры.2) Сформулируй основные свойства площадей геометрических фигур.3) Как можно вычислить площадь прямоугольника и параллелограмма?
Слайды и текст этой презентации
Слайд 1Площадь треугольника
Полезные теоремы, следствия и задачи.
Бойко Вера Петровна
. учитель математики
Слайд 2Вспомните ответы на вопросы
1) Сформулируй понятие площади геометрической фигуры.
2) Сформулируй
основные свойства площадей геометрических фигур.
3) Как можно вычислить площадь прямоугольника
и параллелограмма?Слайд 3Площадь геометрической фигуры
Площадью геометрической фигуры
называется величина,
характеризующая размер данной
фигуры.
Слайд 4Основные свойства площадей геометрических фигур
- Любая плоская геометрическая фигура имеет
площадь.
- Эта площадь – единственная.
- Площадь любой геометрической фигуры выражается
положительным числом.- Площадь квадрата со стороной,равной единице,равна единице.
- Площадь фигуры равна сумме площадей частей,на которые она разбивается.
Слайд 5Площадь прямоугольника
Площадь прямоугольника равна
произведению двух его соседних сторон.
в
S =
а · в
Слайд 6Площадь параллелограмма
Площадь параллелограмма равна
произведению его стороны на высоту,
опущенную
на эту сторону
а
S = а · h
h
Слайд 7Площадь параллелограмма
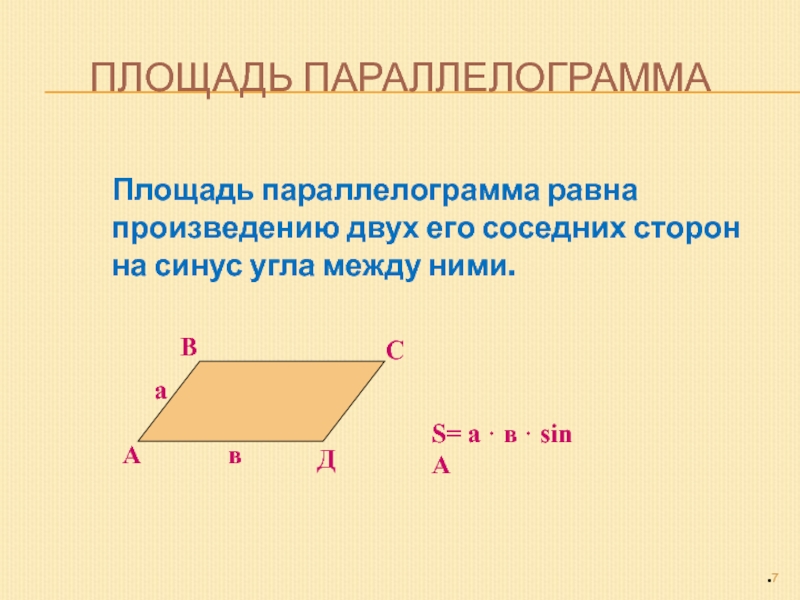
Площадь параллелограмма равна
произведению двух его соседних сторон
на
синус угла между ними.
а
в
А
В
С
Д
S= а · в · sin А
Слайд 8Площадь треугольника
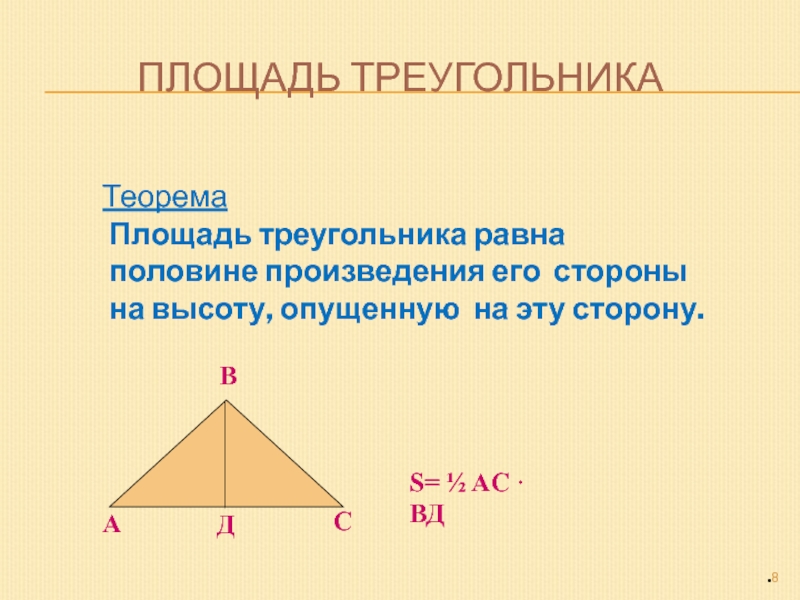
Теорема
Площадь треугольника равна
половине произведения
его стороны
на высоту, опущенную на эту сторону.
А
В
С
Д
S= ½ AC
· ВДСлайд 11Следствие 1
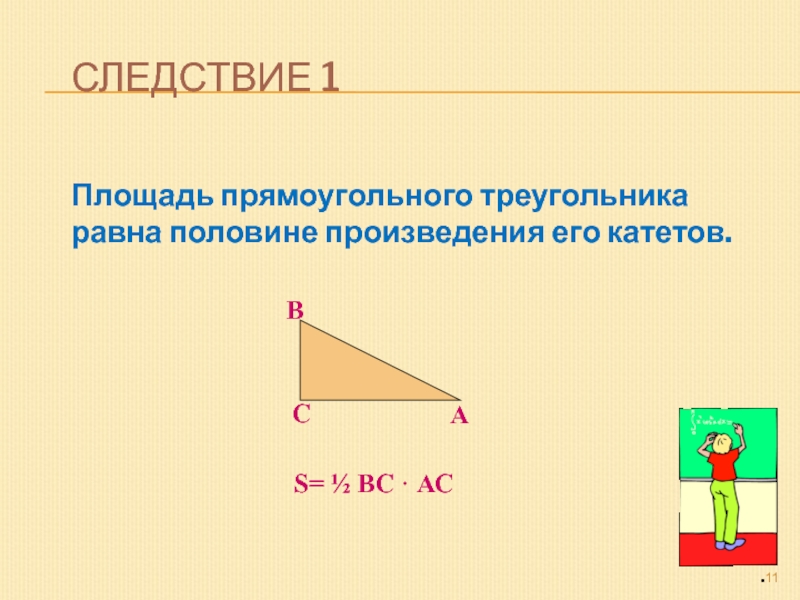
Площадь прямоугольного треугольника
равна половине произведения его катетов.
А
В
С
S= ½
ВС · АС
Слайд 12Следствие 2
Площадь тупоугольного треугольника
равна произведению любой из его сторон
на высоту, опущенную на прямую,
содержащую эту сторону.
А
В
С
Д
Слайд 13Следствие 3
Площадь треугольника равна
половине произведения двух любых его сторон
на синус угла между ними.
А
В
С
S= ½ АВ · АС ·
sin АСлайд 14Следствие 4
Площадь равностороннего треугольника вычисляется по формуле:
где а – сторона
треугольника
Слайд 15Сначала реши легкие задачки
1. Найти площадь треугольника, основание которого равно
16 см,
а высота, опущенная на это
основание, равна 20 см.2. Найти площадь равностороннего треугольника со стороной 6 см.
3. Найти площадь прямоугольного треугольника, катеты которого равны
9 см и 12 см.
Слайд 17Теперь реши задачки потруднее
1. В равнобедренном треугольнике боковая сторона равна
13 см, а основание равно 10 см. Найдите площадь треугольника.
2.
Дан равносторонний треугольник со стороной а. Найти площадь треугольника, составленного из средних линий данного треугольника.3. Гипотенуза прямоугольного треугольника равна 10 см, а один из его катетов
равен 8 см. Найдите площадь этого прямоугольного треугольника
Слайд 18Теперь реши самые трудные задачи
1. Боковая сторона равнобедренного треугольника равна
a, а угол при основании равен . Найдите площадь треугольника.
2.
Высота равностороннего треугольника равна h. Вычислите его площадь.3. В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен . Найдите площадь треугольника.
Слайд 22Это интересно!
Определение площадей геометрических фигур - одна из древнейших
практических задач.
Правильный подход к их решению был найден не сразу. Один из самых простых и доступных способов вычисления площадей был открыт Евклидом. При вычислении площадей он использовал простой прием, называемый методом разбиения.
Слайд 23 Например, мы уже знаем, как можно
вычислить площадь квадрата, прямоугольника и параллелограмма, а нам нужно вычислить
площадь произвольного треугольника. Применим следующий алгоритм:Слайд 24-Отметим на одной из сторон треугольника точку, которая является серединой
этой стороны.
-Проведем через эту точку прямую, параллельную одной из сторон
этого треугольника.-Прямая разбивает этот треугольник на малый треугольник и трапецию.
-Переставим меньший треугольник к трапеции так, чтобы получился параллелограмм.
Слайд 26 Исходный треугольник и полученный параллелограмм являются равносоставными
фигурами, а значит и равновеликими.Мы знаем, что равновеликие фигуры -
это фигуры, имеющие равные площади. Значит площадь исходного треугольника равна площади полученного параллелограмма.Слайд 27 Площадь параллелограмма равна произведению его
основания на высоту, а высота исходного треугольника по построению в
2 раза больше высоты параллелограмма. Значит площадь треугольника равна половине произведения его основания на высоту!Слайд 28И в заключении…
Надеюсь, что эта информация поможет вам хорошо разобраться
в этой теме, а значит получить на контрольной работе только
«5»!Благодарю за внимание !