Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные способы доказательства теоремы Пифагора
Содержание
- 1. Различные способы доказательства теоремы Пифагора
- 2. a2+b2=c2cabП
- 3. Пифагор не открыл это свойство прямоугольного
- 4. Слайд 4
- 5. Доказательства, основанные на использовании понятия равновеликости фигур.
- 6. Ясно, что если от площади квадрата отнять
- 7. Аддитивные доказательства.Эти доказательства основаны на разложении квадратов,
- 8. На рис. 4 приведено доказательство теоремы Пифагора
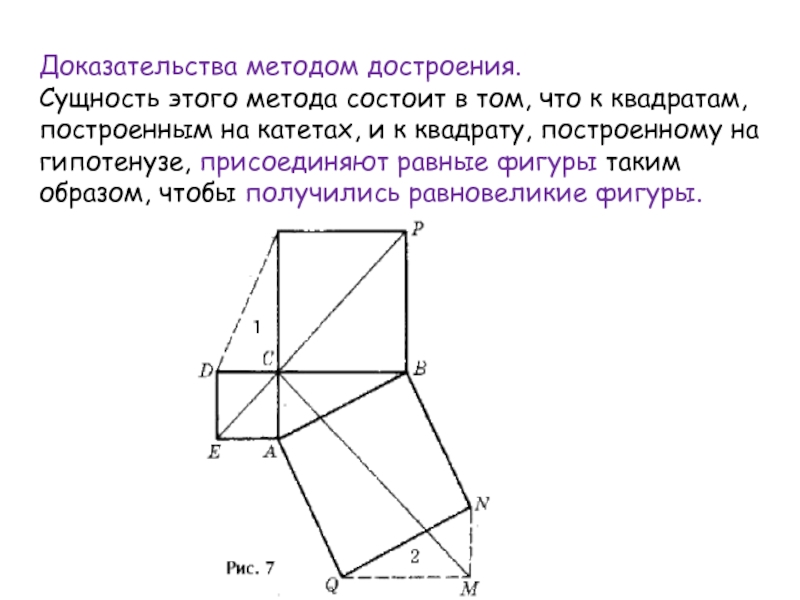
- 9. Доказательства методом достроения. Сущность этого метода состоит
- 10. Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. F
- 11. На рис. 13 ABC – прямоугольный, C
- 12. На рисунке 15 три прямоугольных треугольника составляют
- 13. Биография Пифагора . Великий ученый Пифагор родился
- 14. Изучив язык и религию египтян, он уезжает
- 15. А на Самосе в то время царствовал
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Различные способы доказательства теоремы Пифагора
По материалам Интернета исследование провела учитель
математики МКОУ Букреевской основной общеобразовательной школы Педенко Виктория Александровна.
Слайд 3 Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно,
первым сумел его обобщить и доказать, перевести тем самым из
области практики в область науки. Мы не знаем, как он это сделал. Предполагается, что все же доказательство Пифагора было не принципиальным, а лишь подтверждением, проверкой этого свойства на ряде частных видов треугольников, начиная с равнобедренного прямоугольного треугольника, для которого оно очевидно следует из рис. 1.Слайд 6Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного
треугольника с катетами a, b, то останутся равные площади, т.
е. c2 = a2 + b2. Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «смотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.Слайд 7Аддитивные доказательства.
Эти доказательства основаны на разложении квадратов, построенных на катетах,
на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.
Доказательство Эйнштейна (рис. 3) основано на разложении квадрата, построенного на гипотенузе, на 8 треугольников.
Слайд 8На рис. 4 приведено доказательство теоремы Пифагора с помощью разбиения
ан-Найризия – средневекового багдадского комментатора «Начал» Евклида. В этом разбиении
квадрат, построенный на гипотенузе, разбит на 3 треугольника и 2 четырехугольника. Здесь: ABC – прямоугольный треугольник с прямым углом C; DE = BF.Докажите теорему с помощью этого разбиения.
D
E
Слайд 9Доказательства методом достроения.
Сущность этого метода состоит в том, что
к квадратам, построенным на катетах, и к квадрату, построенному на
гипотенузе, присоединяют равные фигуры таким образом, чтобы получились равновеликие фигуры.Слайд 10Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ.
F
Слайд 11На рис. 13 ABC – прямоугольный, C – прямой угол,
CM AB, b1 – проекция катета b на гипотенузу,
a1 – проекция катета a на гипотенузу, h – высота треугольника, проведенная к гипотенузе.Из того, что ABC подобен ACM, следует, что
b2 = c*b1; (1)
из того, что ABC подобен BCM, следует, что
a2 = c*a1. (2)
Складывая почленно равенства (1) и (2), получим a2 + b2 = c*b1 + c*a1 = c*(b1 + a1) = c2.
b
Слайд 12На рисунке 15 три прямоугольных треугольника составляют трапецию. Поэтому площадь
этой фигуры можно находить по формуле площади прямоугольной трапеции, либо
как сумму площадей трех треугольников.Доказательство Гарфилда.
Слайд 13
Биография Пифагора . Великий ученый Пифагор родился около 570 г.
до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик
по драгоценным камням. Имя же матери Пифагора не известно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора были старец Гермодамант и Ферекид Сиросский. Целые дни проводил юный Пифагор у ног старца Гермо, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал. В 548 г. до н.э. Пифагор прибыл в Навкратис – самосскую колонию, где было у кого найти кров и пищу.Слайд 14Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря
на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору
свои тайны, предлагая ему сложные испытания. Но, влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была чисто прикладной наукой(удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучится. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину.Слайд 15А на Самосе в то время царствовал тиран Поликрат. Конечно
же, Пифагора не устраивала жизнь придворного полу раба, и он
удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена(«пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас....Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.