Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники. Работа с многогранниками в программе Cabri 3D 10 класс
Содержание
- 1. Многогранники. Работа с многогранниками в программе Cabri 3D 10 класс
- 2. Слайд 2
- 3. «Правильных многогранников вызывающе мало, но этот весьма
- 4. Цели создания проекта: Обучающая цель: Закрепить понятие
- 5. Задачи нашего проекта: Обобщение и систематизация
- 6. Наглядная топология как средство познания реального мираПонятие поверхностиАналитическое задание поверхностиПараметрические уравненияПримеры гомеоморфных поверхностей
- 7. Ход работы:На уроках геометрии ознакомились с многогранникамиИзготовили
- 8. 1 группа «Призмы»Создать презентацию на повторение данной
- 9. Слайд 9
- 10. Призма: основания – равные n – угольники,
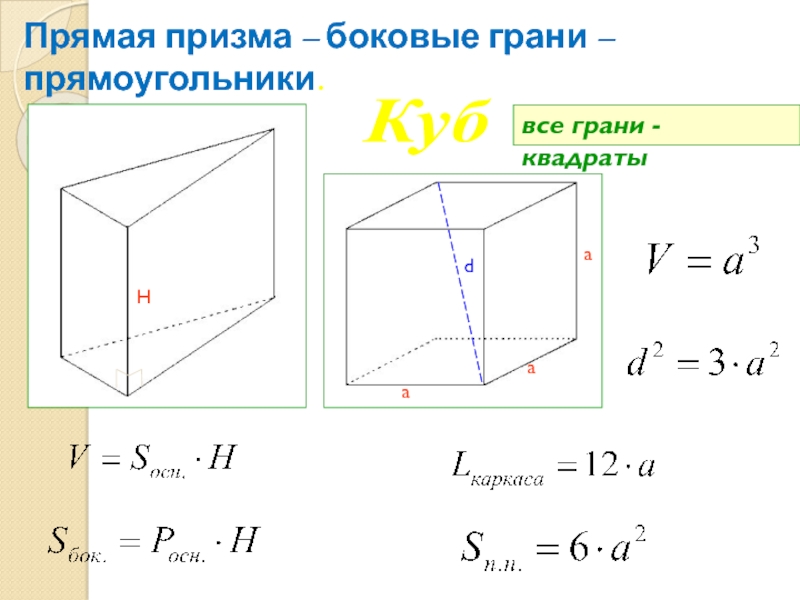
- 11. Прямая призма – боковые грани – прямоугольники. Кубаааdвсе грани - квадратыH
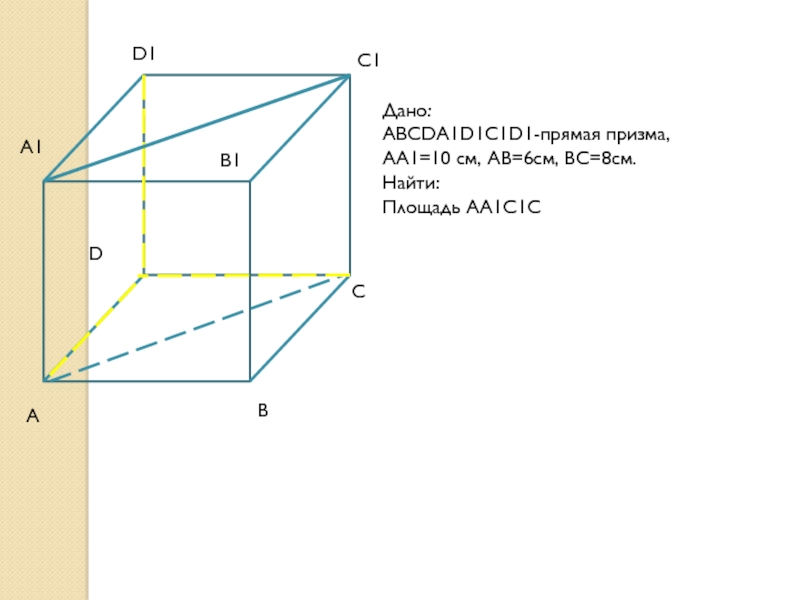
- 12. Дано:ABCDA1D1C1D1-прямая призма, AA1=10 см, AB=6см, BC=8см.Найти:Площадь АА1С1СD1C1CBAA1B1D
- 13. Решение:Диагональные сечения данной призмы равны, так как
- 14. Диагональ куба равна . Найдите его объем.Решение:Диагональ куба
- 15. 2 группа «Пирамиды»Создать презентацию на повторение данной
- 16. Слайд 16
- 17. Пирамида– это многогранник, состоящий из n-угольника А1А2А3...Аn
- 18. Правильная пирамида основание – правильный многоугольник, вершина
- 19. AB = BC = AC = aПравильная треугольная пирамидаH – высота, h – апофема AOBChHSDa
- 20. Правильная четырехугольная пирамидаh – апофема, H –
- 21. PA1A2…An – произвольная пирамидаα – плоскость основанияβ
- 22. Правильная треугольная усеченная пирамида – боковые грани
- 23. Правильная четырехугольная усеченная пирамида – боковые грани
- 24. Задача 1.Основанием пирамиды служит квадрат, две боковые
- 25. Задача №2.Высота и сторона основания правильной четырехугольной пирамиды соответственно равны 24 и 14. Найдите апофему пирамиды.
- 26. Решение. Поскольку пирамида правильная, то в
- 27. 3 группа «Правильные многогранники»Создать презентацию на повторение
- 28. Слайд 28
- 29. Учение о правильных многогранниках
- 30. Многогранник- это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Вспомним
- 31. Выпуклый многогранник называется правильным, если его грани
- 32. ИСТОРИЧЕСКАЯ СПРАВКА.Все эти типы многогранников были известны
- 33. ТЕТРАЭДР.«Тетраэдр» в дословном переводе с греческого языка
- 34. ГЕКСАЭДР.«Гексаэдр» в переводе с греческого языка означает
- 35. ОКТАЭДР.«Октаэдр» в переводе с греческого языка означает
- 36. ДОДЕКАЭДР.«Додекаэдр» в переводе с греческого языка означает
- 37. Многогранники в ювелирном деле
- 38. Многогранники в архитектуре
- 39. 4 группа «Построение сечений многогранников»Создать презентацию на
- 40. Слайд 40
- 41. Определение сечения. Секущей плоскостью многогранника назовем любую
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. АВСSЗадача 1. Построить сечение плоскостью, проходящей через
- 47. Задача 2. Постройте сечение тетраэдра ДАВС
- 48. Спасибо за внимание!
- 49. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Многогранники.
Работа с многогранниками в программе Cabri 3D
10 «а» класс
(хим-био группа)
г.Слайд 3«Правильных многогранников вызывающе мало, но этот весьма скромный по численности
отряд сумел пробраться в самые глубины различных наук».
Л. КэрроллСлайд 4Цели создания проекта:
Обучающая цель: Закрепить понятие о выпуклых многогранниках,
их некоторых свойствах, выработка навыков решения задач на построение сечений
многогранников в программе Cabri 3D, показать связь математики и информатики с жизнью. Повторение формул для вычисления площадей геометрических фигур, площадей поверхностей многогранников; привитие практических навыков решения заданий ЕГЭ; умения работать в программе Cabri 3D.Развивающая цель: формирование компетентности в сфере самостоятельной познавательной деятельности, навыков самостоятельной работы с большим объёмом информации, формирование навыков работы в команде, развитие творческих способностей личности, умений сравнивать, выявлять закономерности; развитие логического мышления, памяти и математической речи; графической культуры.
Слайд 5
Задачи нашего проекта:
Обобщение и систематизация знаний
Расширение спектра задач, доступных учащимся
Формирование
у учащихся устойчивого интереса к геометрии и информатике, выявление способностей
учащихся к данным предметамОриентация на профессию, существенным образом связанную с математикой и информатикой, подготовка к сдаче ЕГЭ и обучению в ВУЗе
Слайд 6Наглядная топология как средство познания реального мира
Понятие поверхности
Аналитическое задание поверхности
Параметрические
уравнения
Примеры гомеоморфных поверхностей
Слайд 7Ход работы:
На уроках геометрии ознакомились с многогранниками
Изготовили модели правильных многогранников
Составили
и решили задачи разного типа на тему «Многогранники»
Разделились на 4
группы:Слайд 81 группа «Призмы»
Создать презентацию на повторение данной темы: определение призмы,
виды призм, элементы призмы, формулы для вычисления площади поверхности призмы
(боковой и полной)Научиться строить призму в программе Cabri 3D
Составить и решить 3 задачи на применение формул для вычисления площади призмы, изготовить модель фигуры.
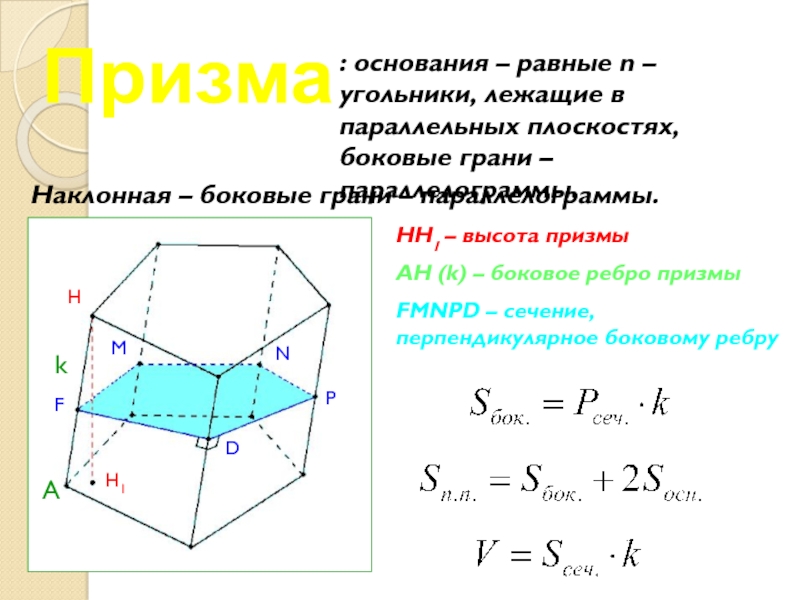
Слайд 10Призма
: основания – равные n – угольники, лежащие в параллельных
плоскостях, боковые грани – параллелограммы.
Наклонная – боковые грани –
параллелограммы.H
H1
A
k
F
M
N
P
D
HH1 – высота призмы
AH (k) – боковое ребро призмы
FMNPD – сечение, перпендикулярное боковому ребру
Слайд 13Решение:
Диагональные сечения данной призмы равны, так как равны диагонали основания
и боковые ребра.
Диагональное сечение АА1С1С-прямоугольник. Сторона АС есть диагональ основания
ABCD. Из прямоугольного тр-ка АВС по теореме ПифагораАС= 6^2 + 8^2= 10 см. Поэтому
Saa1c1c=10*10=100 см^2
Ответ:100см^2
Слайд 14Диагональ куба равна .
Найдите его объем.
Решение:
Диагональ куба в раз
больше его ребра. Получим, что ребро равно
a=Тогда объем куба V= a3 = 8
Ответ: 8
Слайд 152 группа «Пирамиды»
Создать презентацию на повторение данной темы: определение пирамиды,
виды пирамид, элементы пирамид, формулы для вычисления площади поверхности пирамиды
(боковой и полной).Научиться строить пирамиду в программе Cabri 3D
Составить и решить 3 задачи на применение формул для вычисления площади пирамиды, изготовить модель фигуры.
Слайд 17Пирамида
– это многогранник, состоящий из n-угольника А1А2А3...Аn (основание) и n
треугольников (боковые грани), имеющих общую вершину (Р).
Р
А1
А2
А3
Аn
H
РА1; РА2; РА3;
... ; РАn – боковые ребраА1А2; ... ;А1Аn – ребра основания
РH – высота пирамиды - h
h
Слайд 18Правильная пирамида
основание – правильный многоугольник, вершина проецируется в центр
основания;
боковые ребра – равны;
боковые грани – равные равнобедренные
треугольники. H – высота,
h – апофема
H
h
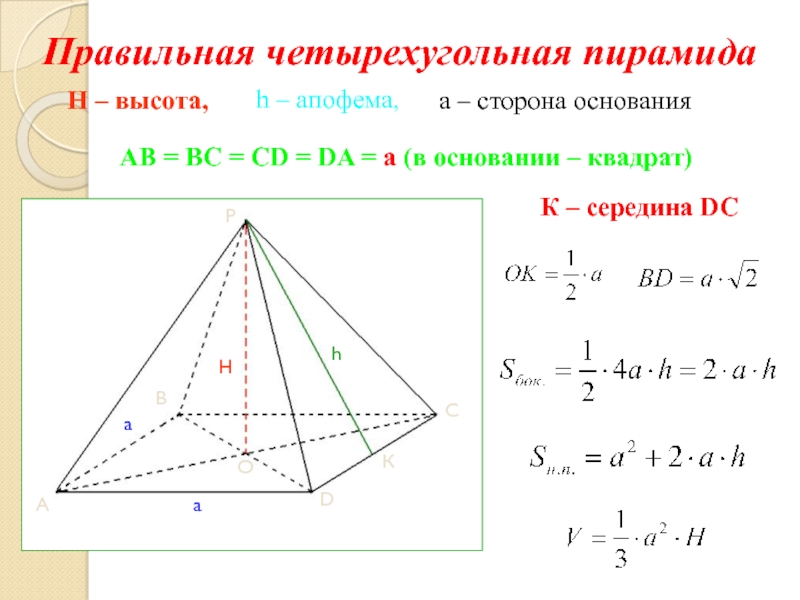
Слайд 20Правильная четырехугольная пирамида
h – апофема,
H – высота,
AB =
BC = CD = DA = a (в основании –
квадрат)H
h
a
a
A
B
D
O
P
К
К – середина DC
C
а – сторона основания
Слайд 21PA1A2…An – произвольная пирамида
α – плоскость основания
β – секущая плоскость,
PB1B2…Bn – пирамида
Усеченная пирамида
β
α
P
A1
A2
A3
An
B1
B3
Bn
B2
O
O1
H
B1B2…Bn – верхнее основание
A1A2…An –
нижнее снованиеA1B1B2A2; …; AnBnB1A1 – боковые грани – трапеции
A1B1; A2B2; …; AnBn – боковые ребра
OO1= H – высота
Слайд 22Правильная треугольная усеченная пирамида –
боковые грани – равные между
собой равнобокие трапеции.
Δ ABC и Δ A1B1C1 – равносторонние
OO1 =
H – высота КК1 = h – апофема
A
C
A1
B1
C1
O1
O
H
K1
K
h
B
a
b
Слайд 23Правильная четырехугольная усеченная пирамида –
боковые грани – равные между
собой равнобокие трапеции.
ABCD и A1B1C1D1 – квадраты
OO1 = H –
высота KK1 = h – апофема
A1
A
B
C
D
B1
C1
D1
O
O1
H
K
K1
h
a
b
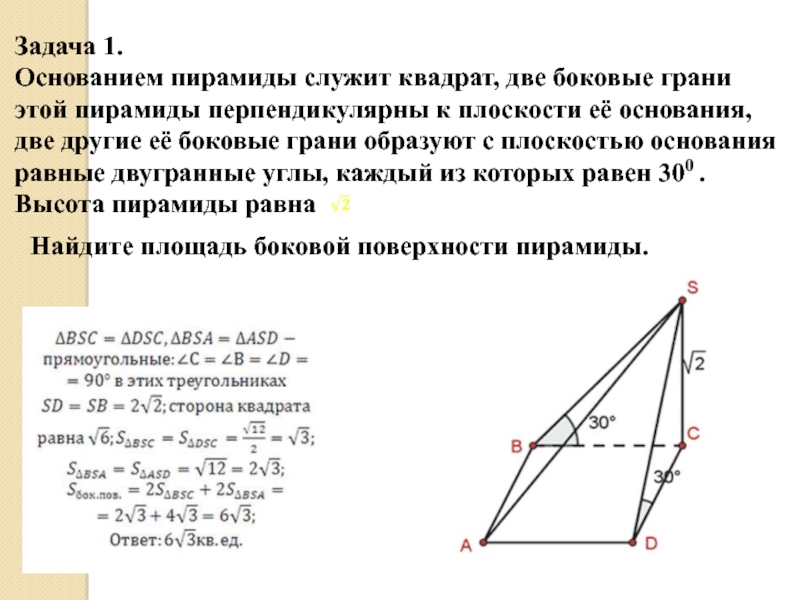
Слайд 24Задача 1.
Основанием пирамиды служит квадрат, две боковые грани
этой пирамиды
перпендикулярны к плоскости её основания,
две другие её боковые грани
образуют с плоскостью основания равные двугранные углы, каждый из которых равен 300 .
Высота пирамиды равна
Найдите площадь боковой поверхности пирамиды.
Слайд 25Задача №2.
Высота и сторона основания правильной четырехугольной пирамиды соответственно равны
24 и 14. Найдите апофему пирамиды.
Слайд 26Решение. Поскольку пирамида правильная, то в ее основании лежит правильный четырехугольник
- квадрат. Кроме того, высота пирамиды проецируется в центр квадрата.
Таким образом, катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды. Откуда по теореме Пифагора длина апофемы будет найдена из уравнения: 72 + 242 = x2 x2 = 625 x = 25 Ответ: 25 смСлайд 273 группа «Правильные многогранники»
Создать презентацию на повторение данной темы: определение
правильных многогранников, виды правильных многогранников,свойства многогранников,объяснение ограниченного количества видов правильных
многогранников.научиться строить развертку данной фигуры в программе Cabri 3D
составить и решить 3 задачи на данную тему, изготовить модель фигуры.
Слайд 29 Учение о правильных многогранниках изложил в своих
трудах Платон. С тех пор правильные многогранники называют Платоновыми телами.
Существует пять видов правильных многогранников: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр.Платон
Слайд 30 Многогранник- это поверхность, составленная из многоугольников и
ограничивающая некоторое геометрическое тело.
Вспомним
Слайд 31Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками
с одним и тем же числом сторон и в каждой
вершине многогранника сходится одно и тоже число ребер.Правильные многогранники еще называют Платоновыми телами.
Существует пять правильных многогранников: 1)тетраэдр, 2)куб, 3)октаэдр, 4)икосаэдр, 5)додекаэдр.
Слайд 32ИСТОРИЧЕСКАЯ СПРАВКА.
Все эти типы многогранников были известны в Древней Греции.
Этим красивым телам посвящена XIII книга «Начал» Евклида. Их называют
еще телами Платона. Они занимали видное место в его идеалистической картине мира. Четыре из них олицетворяют в ней четыре «сущности», или «стихии»: тетраэдр - огонь, икосаэдр - воду, куб - землю, октаэдр - воздух. Додекаэдр воплощал в себе «все сущее»,символизировал все мировоззрение, почитался главнейшим.Слайд 33ТЕТРАЭДР.
«Тетраэдр» в дословном переводе с греческого языка означает «четырехгранник.»У правильного
тетраэдра грани - правильные треугольники; в каждой вершине сходится по
три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.Слайд 34ГЕКСАЭДР.
«Гексаэдр» в переводе с греческого языка означает «шестигранник». У куба
все грани - квадраты; в каждой вершине сходится по три
ребра . Куб представляет собой прямоугольный параллелепипед с равными ребрами.Слайд 35ОКТАЭДР.
«Октаэдр» в переводе с греческого языка означает «восьмигранник». Уоктаэдра грани
- правильные треугольники, но в отличие от тетраэдра в каждой
его вершине сходится по четыре ребра.Слайд 36ДОДЕКАЭДР.
«Додекаэдр» в переводе с греческого языка означает «двенадцатигранник». У додекаэдра
грани - правильные пятиугольники. В каждой вершине сходится по три
ребра.Слайд 394 группа «Построение сечений многогранников»
Создать презентацию на повторение данной темы:
определение сечения, правила их построения
Научиться строить сечения многогранников в
программе Cabri 3DСоставить и решить 3 задачи на построение сечений.
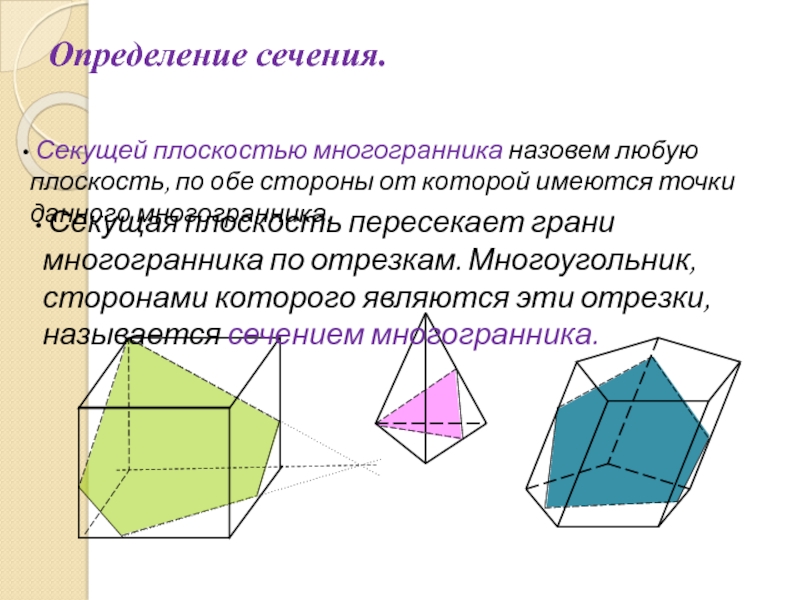
Слайд 41Определение сечения.
Секущей плоскостью многогранника назовем любую плоскость, по обе
стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает
грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.Слайд 46А
В
С
S
Задача 1. Построить сечение плоскостью, проходящей через данные точки D,
Е, K.
D
E
K
M
F
Построение:
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD
∩ BС = M6. KM
1. DE
DЕKМ – искомое сечение
Слайд 47Задача 2. Постройте сечение тетраэдра ДАВС плоскостью, проходящей через
точки К є ВС , М є АДВ, N є
ВДС. Решение
1. М → М1 , N → N1
2. Х = NМ ∩ N1 М1
3. R = КХ ∩ АВ
RL = α ∩ АВД,
М є RL
КР = α ∩ ВДС,
N є КР
6. LP = α ∩ АДС
7. RLPK - искомое сечение