Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Содержание
- 1. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
- 2. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Для того чтобы убрать
- 3. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Изображение додекаэдра можно поворачивать,
- 4. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Для устранения окраски граней
- 5. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»В программе «Математика» имеется
- 6. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Операцию усечения можно производить
- 7. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Помимо операции усечения, в
- 8. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Операцию “Stellate” тоже можно
- 9. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Операции “Truncate” и “Stellate” можно комбинировать. Например, команда
- 10. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Команда
- 11. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Для получения изображения графика
- 12. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Если вместо x^2+y^2 в
- 13. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»КомандаPlot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]Приведет к графику функции z= sin(xy).
- 14. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»КомандаPlot3D[Sin[x]*Sin[y], {x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]Приведет к графику функции z= sin(x)sin(y).
- 15. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Программа «Математика» позволяет получать
- 16. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Для получения поверхности вращения
- 17. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Если вместо Sin[x] в
- 18. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Если вместо Sin[x] подставить
- 19. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Вращать можно не только
- 20. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Некоторые поверхности программа «Математика» имеет в своей памяти. Так, если набрать
- 21. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»В квадратных скобках можно
- 22. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Cylinder,
- 23. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» В квадратных скобках можно
- 24. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Cone,
- 25. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Torus,
- 26. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо Helix, написать MoebiusStrip, то получим изображения листа Мебиуса.
- 27. Скачать презентанцию
ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Для того чтобы убрать куб, к команде следует добавитьBoxed->False и нажать клавиши SHIFT и ENTER
Слайды и текст этой презентации
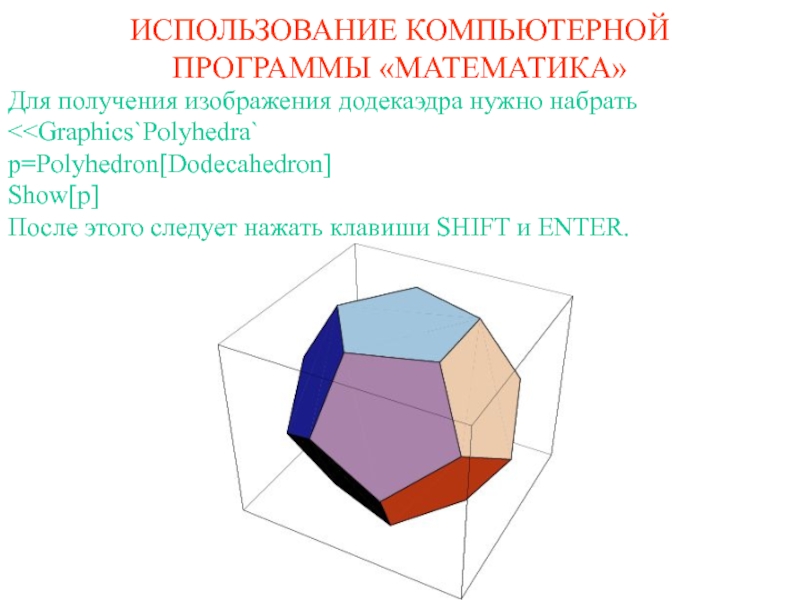
Слайд 1ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Для получения изображения додекаэдра нужно набрать
этого следует нажать клавиши SHIFT и ENTER.
Слайд 2ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Для того чтобы убрать куб, к команде
следует добавить
Boxed->False и нажать клавиши SHIFT и ENTER
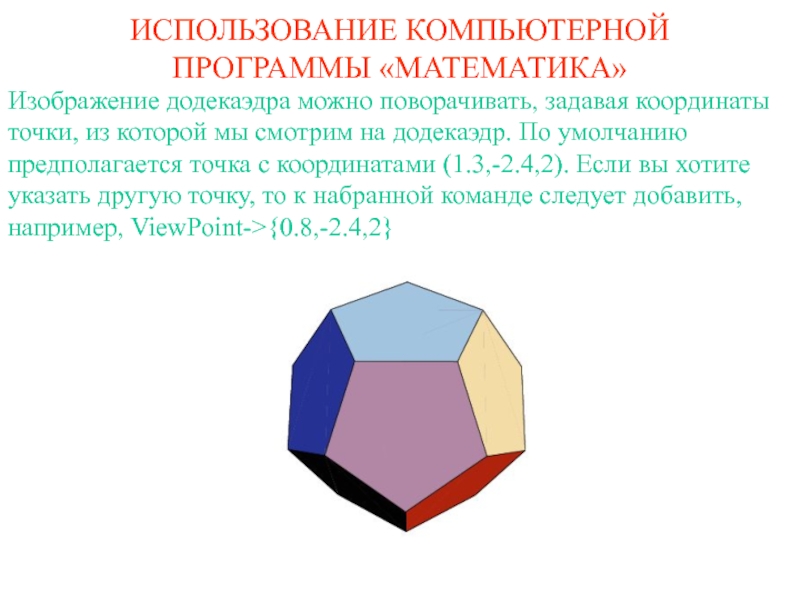
Слайд 3ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Изображение додекаэдра можно поворачивать, задавая координаты точки,
из которой мы смотрим на додекаэдр. По умолчанию предполагается точка
с координатами (1.3,-2.4,2). Если вы хотите указать другую точку, то к набранной команде следует добавить, например, ViewPoint->{0.8,-2.4,2}Слайд 4ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Для устранения окраски граней додекаэдра следует добавить
Shading->False.
В результате получим команду
False]
исполнение которой приведет к рисунку
Если вместо Dodecahedron
написать соответственно Tetrahedron, Hexahedron, Octahedron, Icosahedron, то получим изображения тетраэдра, куба, октаэдра и икосаэдра.Слайд 5ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
В программе «Математика» имеется операция “Truncate”, при
которой от правильных многогранников отсекаются углы и в результате получаются
полуправильные многогранники. Так, например, исполнение команды<
Show[Truncate[p],Boxed->False]
приводит к усеченному додекаэдру.
Слайд 6ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Операцию усечения можно производить с заданным коэффициентом,
показывающим какая часть ребра отсекается. Так, например, если выбрать коэффициент,
равным 0.5 , то исполнение соответствующей команды<
Show[Truncate[p,0.5],Boxed->False]
приводит к икосододекаэдру.
Слайд 7ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Помимо операции усечения, в программа «Математика» имеется
операция “Stellate”, которая приводит к звездчатым многогранникам. Так, например, исполнение
команды<
Show[Stellate[p,2.2],Boxed->False]
приводит к малому звездчатому
додекаэдру.
Слайд 8ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Операцию “Stellate” тоже можно производить с разными
коэффициентами. Если коэффициент меньше единицы, то она производится вовнутрь многогранника.
Например, исполнение команды<
Show[Stellate[p,0.7],Boxed->False]
приводит к большому додекаэдру.
Слайд 9ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Операции “Truncate” и “Stellate” можно комбинировать. Например,
команда
Слайд 11ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
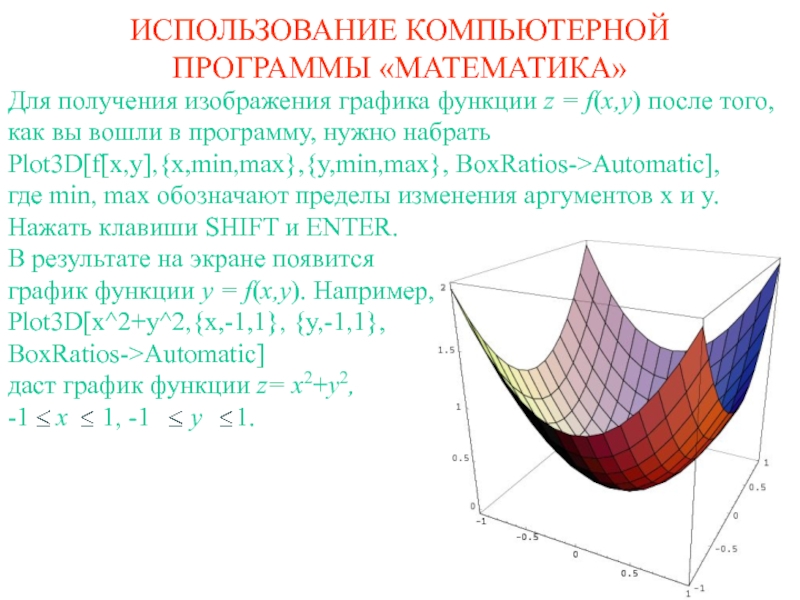
Для получения изображения графика функции z =
f(x,y) после того, как вы вошли в программу, нужно набрать
Plot3D[f[x,y],{x,min,max},{y,min,max},
BoxRatios->Automatic],где min, max обозначают пределы изменения аргументов x и y.
Нажать клавиши SHIFT и ENTER.
В результате на экране появится
график функции y = f(x,y). Например,
Plot3D[x^2+y^2,{x,-1,1}, {y,-1,1},
BoxRatios->Automatic]
даст график функции z= x2+y2,
-1 x 1, -1 y 1.
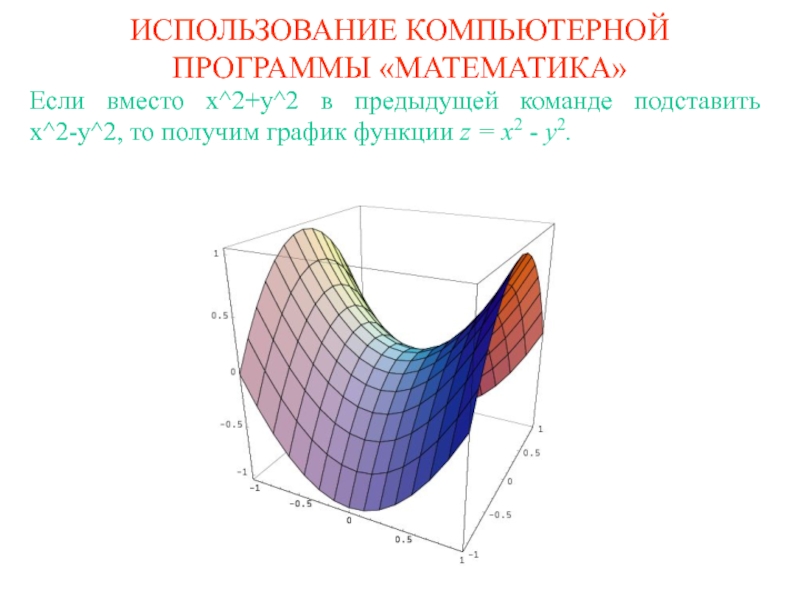
Слайд 12ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Если вместо x^2+y^2 в предыдущей команде подставить
x^2-y^2, то получим график функции z = x2 - y2.
Слайд 13ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Команда
Plot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]
Приведет к графику функции z= sin(xy).
Слайд 14ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Команда
Plot3D[Sin[x]*Sin[y], {x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]
Приведет к графику функции z=
sin(x)sin(y).
Слайд 15ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
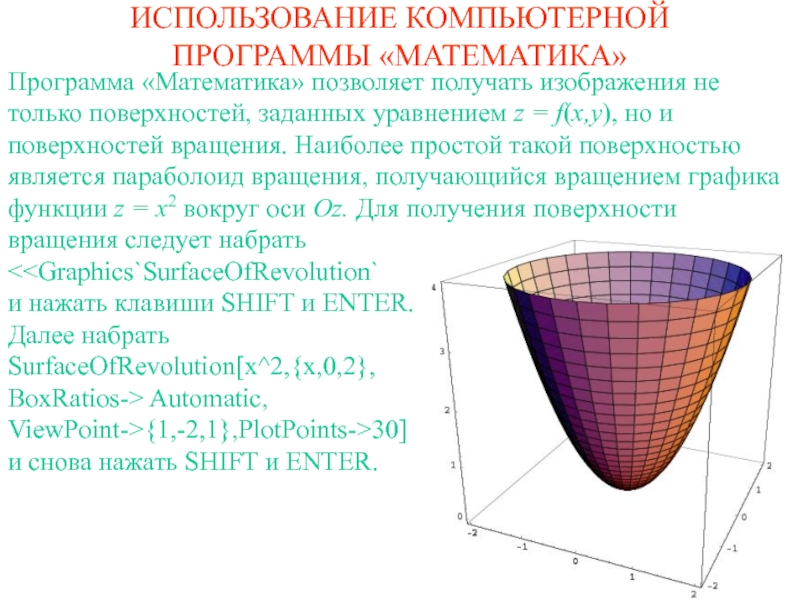
Программа «Математика» позволяет получать изображения не только
поверхностей, заданных уравнением z = f(x,y), но и поверхностей вращения.
Наиболее простой такой поверхностью является параболоид вращения, получающийся вращением графика функции z = x2 вокруг оси Oz. Для получения поверхности вращения следует набрать<
Далее набрать
SurfaceOfRevolution[x^2,{x,0,2},
BoxRatios-> Automatic,
ViewPoint->{1,-2,1},PlotPoints->30]
и снова нажать SHIFT и ENTER.
Слайд 16ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
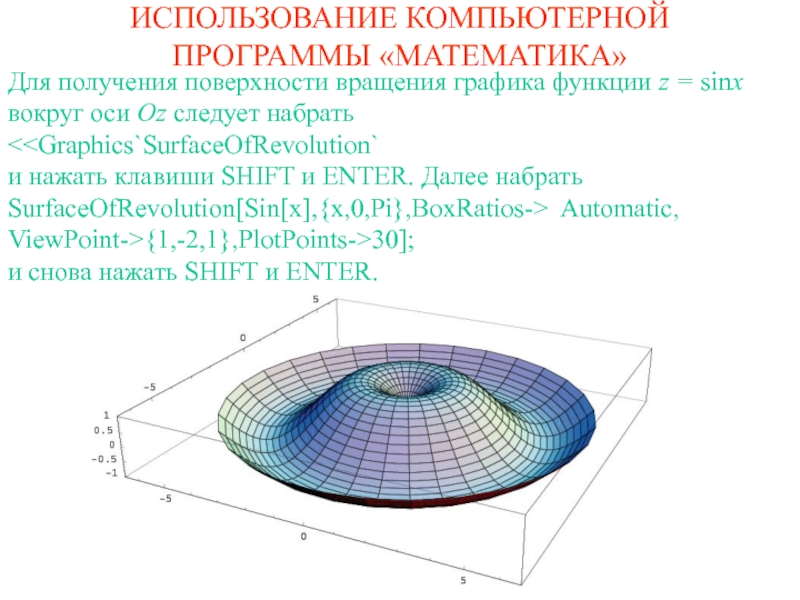
Для получения поверхности вращения графика функции z
= sinx вокруг оси Oz следует набрать
SHIFT и ENTER. Далее набрать SurfaceOfRevolution[Sin[x],{x,0,Pi},BoxRatios-> Automatic,
ViewPoint->{1,-2,1},PlotPoints->30];
и снова нажать SHIFT и ENTER.
Слайд 17ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Если вместо Sin[x] в предыдущей команде набрать
Exp[x] и в качестве пределов изменения x поставить {x,-1,1}, то
получится поверхность вращения графика функции z = ex.Слайд 18ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Если вместо Sin[x] подставить 1/x и пределы
изменения x взять от 0,25 до 2, то получим поверхность
вращения, изображенную на рисунке.Слайд 19ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
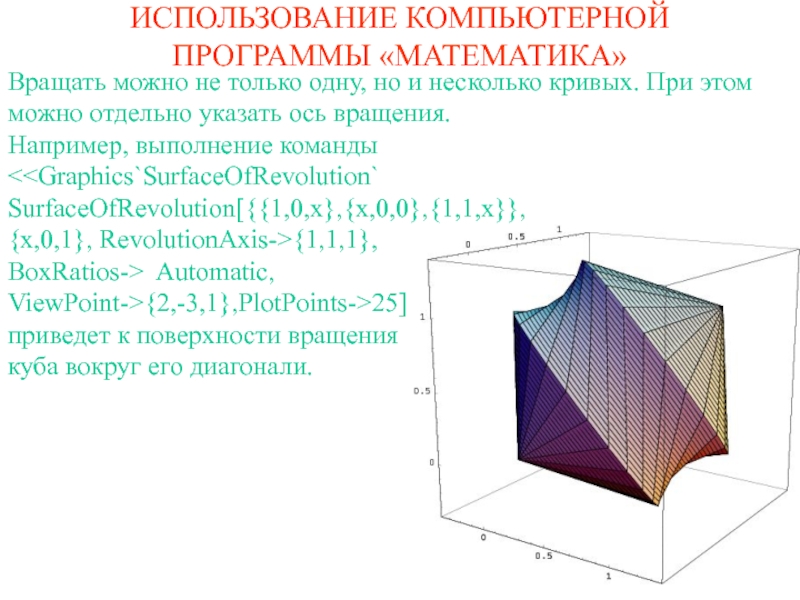
Вращать можно не только одну, но и
несколько кривых. При этом можно отдельно указать ось вращения.
Например,
выполнение команды<
{x,0,1}, RevolutionAxis->{1,1,1},
BoxRatios-> Automatic,
ViewPoint->{2,-3,1},PlotPoints->25]
приведет к поверхности вращения
куба вокруг его диагонали.
Слайд 20ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Некоторые поверхности программа «Математика» имеет в своей
памяти. Так, если набрать
то подгрузится пакет, содержащий некоторые стандартные поверхности. Если далее набрать
Show[Graphics3D[Cylinder[]],
Boxed->False],
и снова нажать SHIFT и ENTER,
то в результате получим изображение
боковой поверхности цилиндра.
Слайд 21ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
В квадратных скобках можно указать величину радиуса
основания, высоты и числа вершин многоугольника в основании цилиндра. Например,
исполнение командыShow[Graphics3D[Cylinder[2,1,6]],Boxed->False]
приводит к боковой поверхности прямой шестиугольной призмы.
Слайд 22ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
Если вместо слова Cylinder, написать слово Cone,
т.е. набрать
Show[Graphics3D[Cone[]],Boxed->False]
и снова нажать SHIFT и ENTER, то в результате
получим изображение поверхности конуса.Слайд 23ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»
В квадратных скобках можно указать величину радиуса
основания, высоты и числа вершин многоугольника в основании конуса. Например,
исполнение командыShow[Graphics3D[Cone[2,1,6]],Boxed->False]
приводит к поверхности прямой шестиугольной пирамиды.

![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Для устранения окраски граней додекаэдра следует добавитьShading->False. В ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Для устранения окраски граней додекаэдра следует добавитьShading->False. В результате получим командуFalse]исполнение которой приведет к](/img/thumbs/58484fa40d624c137c7e8b810b439173-800x.jpg)






![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»КомандаPlot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]Приведет к графику функции z= sin(xy). ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»КомандаPlot3D[Sin[x*y],{x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]Приведет к графику функции z= sin(xy).](/img/tmb/2/168700/fa28806802239eeb673927e4539285ec-800x.jpg)
![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»КомандаPlot3D[Sin[x]*Sin[y], {x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]Приведет к графику функции z= sin(x)sin(y). ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»КомандаPlot3D[Sin[x]*Sin[y], {x,-Pi,Pi}, {y,-Pi,Pi},BoxRatios->Automatic]Приведет к графику функции z= sin(x)sin(y).](/img/thumbs/e2d547fa9a4953e87f8ebb127010b6cd-800x.jpg)
![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Если вместо Sin[x] в предыдущей команде набрать Exp[x] ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Если вместо Sin[x] в предыдущей команде набрать Exp[x] и в качестве пределов изменения x](/img/thumbs/9f98032e535d00a4b1bac739d20595d7-800x.jpg)
![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Если вместо Sin[x] подставить 1/x и пределы изменения ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА»Если вместо Sin[x] подставить 1/x и пределы изменения x взять от 0,25 до 2,](/img/thumbs/0c256d4f824f2260435de6dfc41bc51f-800x.jpg)


![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Cylinder, написать слово Cone, т.е. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Cylinder, написать слово Cone, т.е. набратьShow[Graphics3D[Cone[]],Boxed->False]и снова нажать SHIFT и ENTER,](/img/thumbs/ff9c62228d190b5593042f8f8a17653d-800x.jpg)

![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Cone, написать слово Torus, т.е. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Cone, написать слово Torus, т.е. набратьShow[Graphics3D[Torus[]],Boxed->False]и снова нажать SHIFT и ENTER,](/img/thumbs/a86d8c24c80edd07a5ad1b8af914b596-800x.jpg)
![ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Torus, написать слово Helix, т.е. ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНОЙ ПРОГРАММЫ «МАТЕМАТИКА» Если вместо слова Torus, написать слово Helix, т.е. набратьShow[Graphics3D[Helix[]],Boxed->False]и снова нажать SHIFT и ENTER,](/img/thumbs/e85b47c2550b920002c4cf8502d1172c-800x.jpg)