Четырехугольник и его элементы 8 класс

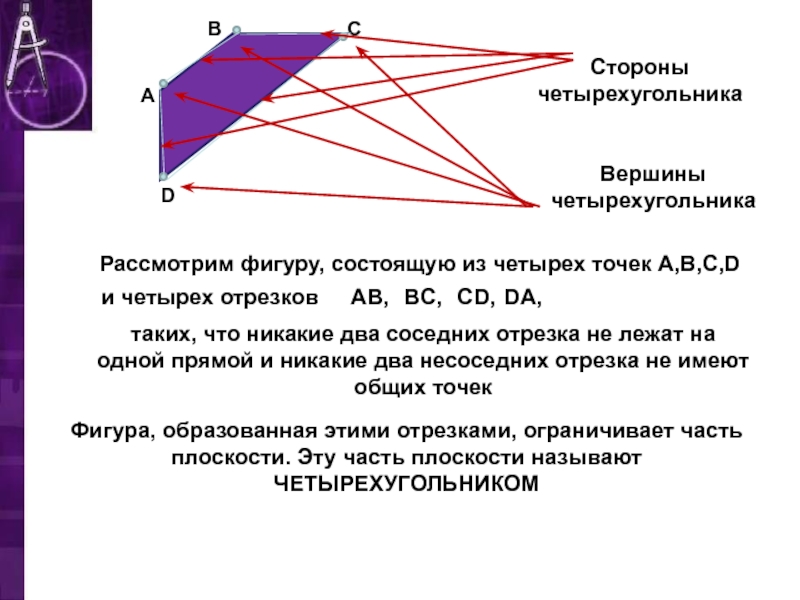
что никакие два соседних отрезка не лежат на одной прямой

Фигура, образованная этими отрезками, ограничивает часть плоскости. Эту часть плоскости называют ЧЕТЫРЕХУГОЛЬНИКОМ

Вершины четырехугольника

Стороны четырехугольника

являющиеся концами одной стороны, называют соседними вершинами четырехугольника
Стороны четырехугольника, не

Несоседние вершины четырехугольника, называют противолежащими вершинами четырехугольника

Отрезок, соединяющий противолежащие вершины четырехугольника, называют диагональю четырехугольника

соседними, противолежащими?

вершин;
4.пары противолежащих вершин;
5.пары соседних сторон;
6.пары противолежащих сторон.

меньше развернутого угла.
Такой четырехугольник называют выпуклым.
В четырехугольнике ABCD

Такой четырехугольник не является выпуклым.

АBCD – четырехугольник

Доказать: ˪А+˪В+˪С+˪D=360º

Диагональ BD разбивает четырехугольник на два треугольника.

Сумма углов треугольника равна 180°.

Сумма углов четырехугольника ABCD равна сумме углов треугольников ABD и CBD.

Значит, ˪А+˪В+˪С+˪D=360º

Теорема доказана

равны 78º, 89º и 93º?
100º
Задание. Найдите углы четырехугольника, если они

90º

развернутого
Длина любой стороны четырехугольника меньше суммы длин трех остальных его

Рассмотрим произвольный четырехугольник ABCD

Проведем диагональ AC.

Применяя неравенство треугольника для сторон AB и AC соответственно треугольников ABC и ADC, получаем неравенства:

Решение..

острый;
три прямых угла и один тупой;
четыре прямых угла;
четыре острых угла;
два

Задача. Могут ли стороны четырехугольника быть равными:

2 дм, 3 дм, 4 дм, 9 дм;
2 дм, 3 дм, 4 дм, 10 дм?