Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Паркеты 9 класс
Содержание
- 1. Паркеты 9 класс
- 2. Что такое паркет ?Паркетом называют покрытие плоскости
- 3. Что такое правильный паркет ?Паркет называется правильным,
- 4. Основная задачаЕсли длина стороны многоугольникапаркета задана ,
- 5. Некоторые указания
- 6. 3 многоугольника в вершине6 многоугольниковв вершине4 многоугольника
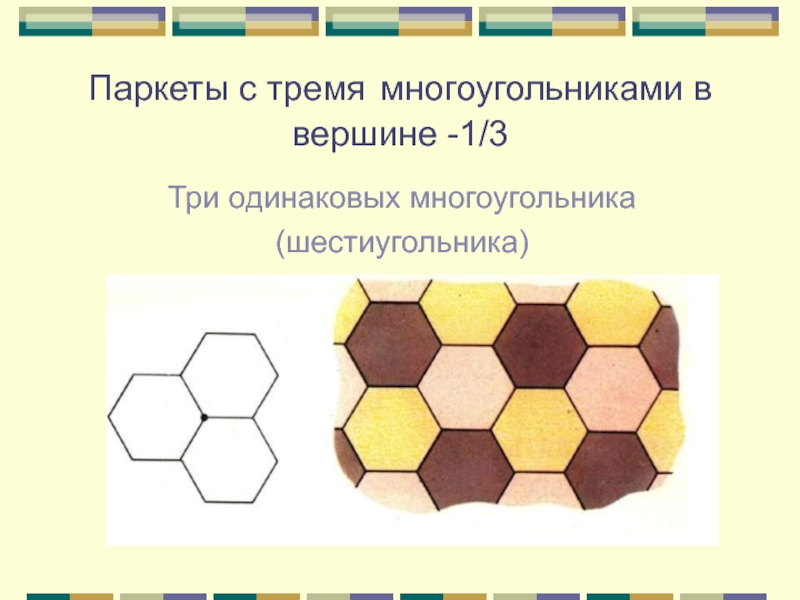
- 7. Паркеты с тремя многоугольниками в вершине -1/3Три одинаковых многоугольника(шестиугольника)
- 8. Паркеты с тремя многоугольниками в вершине
- 9. Паркеты с тремя многоугольниками в вершине– 3/3 Три различных многоугольника:один двенадцати-угольник,один шестиугольник,один квадрат
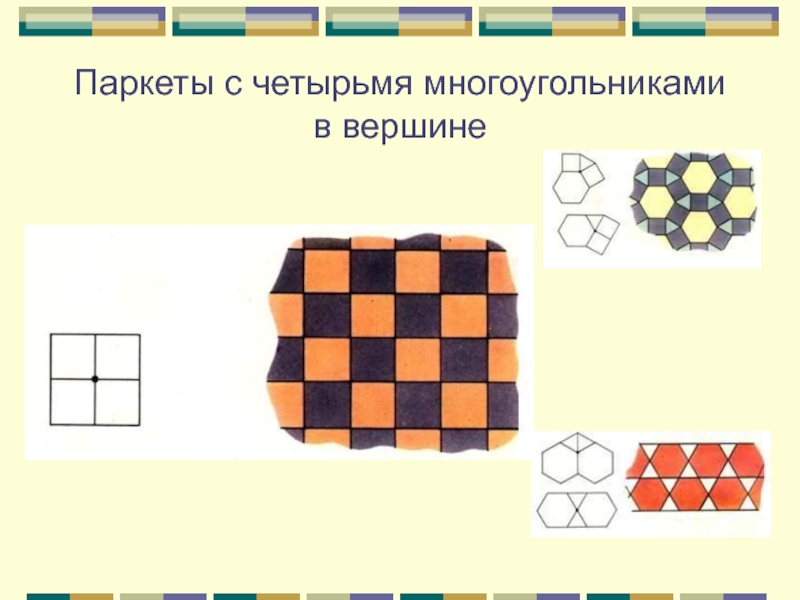
- 10. Паркеты с четырьмя многоугольниками в вершине
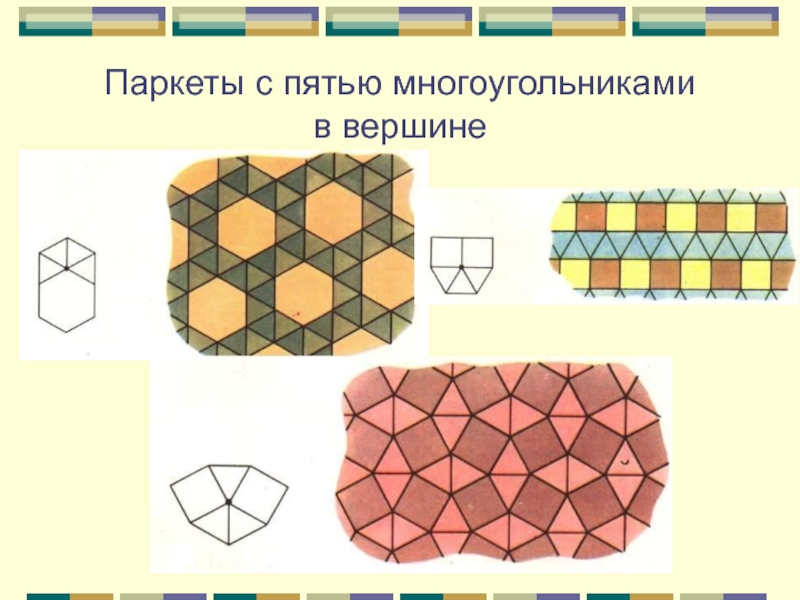
- 11. Паркеты с пятью многоугольниками в вершине
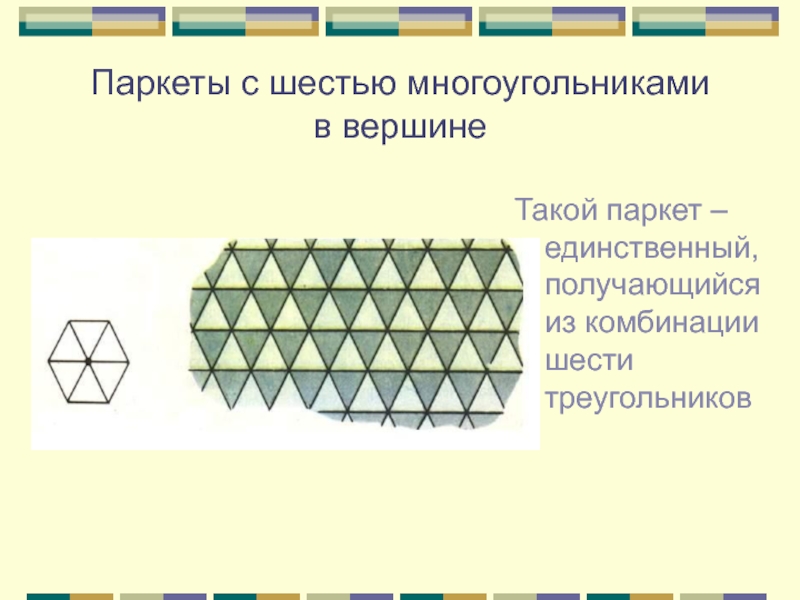
- 12. Паркеты с шестью многоугольниками в вершинеТакой паркет – единственный, получающийся из комбинации шести треугольников
- 13. Паркеты из неправильных выпуклых четырехугольников Олимпиадная задача:Данным
- 14. Паркеты из неправильных невыпуклых четырехугольниковРяд олимпиадных задач решается укладыванием паркета из неправильных невыпуклых четырехугольников
- 15. Другие паркетыБольшие возможности длякомбинаций из плоских фигур открываются при составлении узоров из кафельныхплиток
- 16. Нестрогие паркетыВ том случае, если многоугольники не
- 17. ”Объемные” паркетыОчень интересныепаркеты получаются, если на исходных
- 18. Автор презентацииОрлова Елена СтепановнаЗаместитель директора поУВР средней школы№ 420,учитель математики
- 19. Скачать презентанцию
Что такое паркет ?Паркетом называют покрытие плоскости правильными многоугольниками, при которых два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо совсем не имеют общих точек
Слайды и текст этой презентации
Слайд 1Паркеты
«Все вокруг – геометрия. Дух геометрического и математического порядка станет
властителем архитектурных судеб»
Слайд 2Что такое паркет ?
Паркетом называют покрытие плоскости правильными многоугольниками, при
которых два многоугольника либо имеют общую сторону, либо имеют общую
вершину, либо совсем не имеют общих точек
Слайд 3Что такое правильный паркет ?
Паркет называется правильным, если его можно
наложить на самого себя так, что любая заданная его вершина
наложится на другую заданную его вершину
Слайд 4Основная задача
Если длина стороны многоугольника
паркета задана , то существует только
конечное число различных
( не накладывающихся друг на друга ) правильных
паркетовПеречислить их все и тем самым ответить на вопрос об их числе - это и есть основная задача, которую нам предстоит решить
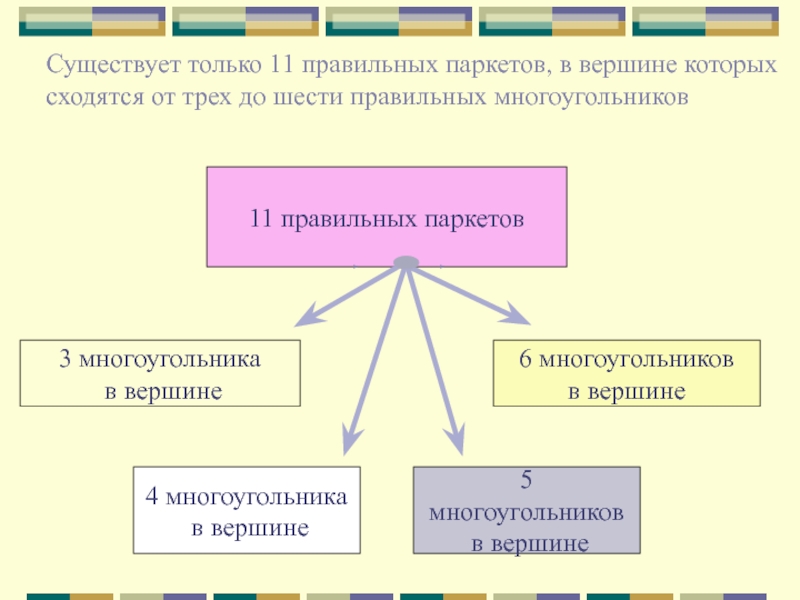
Слайд 63 многоугольника
в вершине
6 многоугольников
в вершине
4 многоугольника
в вершине
5 многоугольников
в вершине
Существует только 11 правильных паркетов, в вершине которых
сходятся
от трех до шести правильных многоугольников11 правильных паркетов
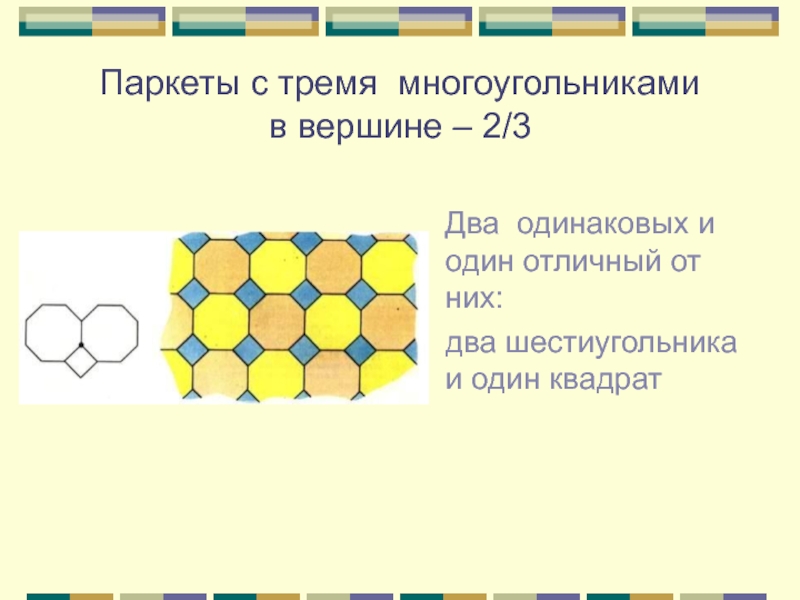
Слайд 8Паркеты с тремя многоугольниками
в вершине – 2/3
Два одинаковых и
один отличный от них:
два шестиугольника и один квадрат
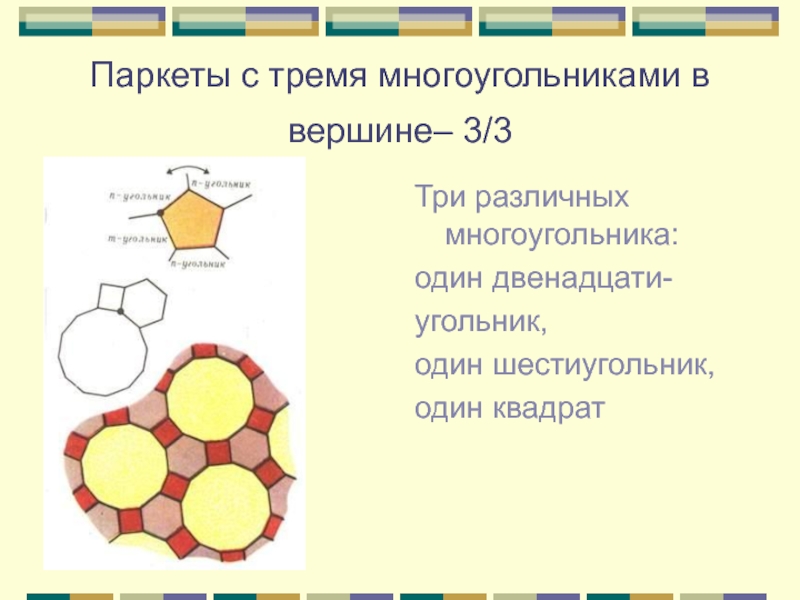
Слайд 9Паркеты с тремя многоугольниками в вершине– 3/3
Три различных многоугольника:
один
двенадцати-
угольник,
один шестиугольник,
один квадрат
Слайд 12Паркеты с шестью многоугольниками
в вершине
Такой паркет – единственный, получающийся из
комбинации шести треугольников
Слайд 13Паркеты из неправильных выпуклых
четырехугольников
Олимпиадная задача:
Данным четырехугольником произвольной
формы настлать паркет, т.
е. заполнить всю
плоскость без пропусков и перекрытий.
Решается с помощью центральной
симметрии.
Отразим
четырехугольник симметричноотносительно середины одной из
сторон. Получим четырехугольник 2.
Теперь четырехугольник 2 отразим
симметрично относительно середины
другой стороны и т.д.
Такое построение можно провести
вокруг каждой вершины каждого из
новых четырехугольников, что и дает
паркет на всей плоскости.
Слайд 14Паркеты из неправильных невыпуклых
четырехугольников
Ряд олимпиадных задач решается укладыванием паркета
из неправильных невыпуклых четырехугольников
Слайд 15Другие паркеты
Большие возможности для
комбинаций из плоских фигур открываются при составлении
узоров из кафельных
плиток
Слайд 16Нестрогие паркеты
В том случае, если многоугольники не примыкают
углом к
углу образуются
зазоры. Но сами эти зазоры
способствуют созданию новых восхитительных
узоров
Слайд 17”Объемные” паркеты
Очень интересные
паркеты получаются, если на исходных фигурах имеется различная
окраска. Она способствует созданию эффекта объема
Картинный зал Петродворца.
Слайд 18Автор презентации
Орлова
Елена Степановна
Заместитель директора по
УВР средней школы
№ 420,
учитель математики
