Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фигуры на плоскости
Содержание
- 1. Фигуры на плоскости
- 2. Содержание:Параллелограмм.Прямоугольник.Ромб.Квадрат.Трапеция.
- 3. ПараллелограммРисунок. Площадь параллелограмма равна произведению его стороны
- 4. Прямоугольник.Рисунок. Прямоугольником называется параллелограмм, у которого все
- 5. РомбРисунок.Ромбом называется параллелограмм, у которого все стороны
- 6. Квадрат.Рисунок. Квадратом называется прямоугольник, у которого все
- 7. Трапеция.Рисунок. Площадь трапецииПлощадь трапеции равна произведению полусуммы
- 8. Скачать презентанцию
Слайды и текст этой презентации
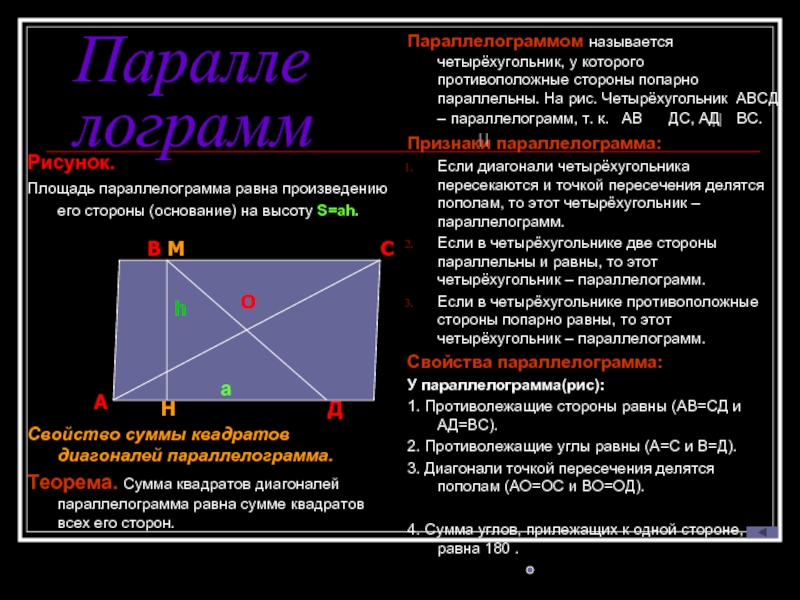
Слайд 3Параллелограмм
Рисунок.
Площадь параллелограмма равна произведению его стороны (основание) на высоту
S=ah.
Свойство суммы квадратов диагоналей параллелограмма.
Теорема. Сумма квадратов диагоналей параллелограмма
равна сумме квадратов всех его сторон.Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны. На рис. Четырёхугольник АВСД – параллелограмм, т. к. АВ ДС, АД ВС.
Признаки параллелограмма:
Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике две стороны параллельны и равны, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Свойства параллелограмма:
У параллелограмма(рис):
1. Противолежащие стороны равны (АВ=СД и АД=ВС).
2. Противолежащие углы равны (А=С и В=Д).
3. Диагонали точкой пересечения делятся пополам (АО=ОС и ВО=ОД).
4. Сумма углов, прилежащих к одной стороне, равна 180 .
О
Д
С
В
А
Н
М
h
а
Слайд 4Прямоугольник.
Рисунок.
Прямоугольником называется параллелограмм, у которого все улы прямые. На
рис. Параллелограмм АВСД – прямоугольник, т. к.
углы А=В=С=Д=90 .
Признаки прямоугольника.
1. Если у параллелограмма один из углов прямой, то этот параллелограмм – прямоугольник.
2. Если у параллелограмма диагонали равны, то этот параллелограмм – прямоугольник.
Свойства прямоугольника.
Прямоугольник имеет все свойства параллелограмма, кроме того, диагонали прямоугольника равны.
Площадь прямоугольника.
Площадь прямоугольника равна произведению двух смежных сторон прямоугольника на (рис). S=ab.
Д
С
В
А
b
a
Слайд 5Ромб
Рисунок.
Ромбом называется параллелограмм, у которого все стороны равны. На рис.
Параллелограмм АВСД – ромб, так как АВ=ВС=СД=ДА.
Признака ромба:
1. Если
у параллелограмма диагонали перпендикулярны, то этот параллелограмм – ромб.2. Если у четырёхугольника стороны равны, то этот четырёхугольник – ромб.
Свойства ромба:
Ромб имеет все свойства параллелограмма, кроме того: 1. Диагонали ромба взаимно перпендикулярны; АС СД.
2. Диагонали ромба являются биссектрисами его углов.
(углы) 1=2=3=4 и 5=6=7=8.
Площадь ромба равна произведению квадрата стороны на синус угла ромба. S=a*а sin a.
Д
С
В
А
1
2
3
4
5
6
7
8
90
Слайд 6Квадрат.
Рисунок.
Квадратом называется прямоугольник, у которого все стороны равны. (Другое
определение: квадратом называется ромб, у которого все углы прямые). На
рис. Изображён квадрат АВСД.Свойства квадрата:
Квадрат имеет все свойства прямоугольника и ромба:
1. У квадрата все углы прямые и все стороны равны.
2. Диагонали квадрата равны и пересекаются под прямым углом.
3. Диагонали квадрата является биссектрисами его углов. Каждая диагональ образует со стороны углов в 45 .
Площадь квадрата равна квадрату его стороны: S=ab.
А
В
С
Д
45
b
a
Слайд 7Трапеция.
Рисунок.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту;
S= a + b*h
Трапецией называется четырёхугольник, у которого две
стороны параллельны. На рис. Четырёхугольник АВСД – трапеция. Параллельные стороны трапеции называются основаниями, а не параллельные стороны – боковыми сторонами. На рис. Стороны ВС и АД – основания, АВ и СД – боковые стороны. Условимся высотой трапеции называть перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащее другое основание. На рис. МН – высота трапеции АВСД. Свойство трапеции:
Сумма углов трапеции, принадлежащих к боковой стороне, равна 180 . На рисунке изображена равнобокая трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции
У равнобокой трапеции:
1.Углы при основании равны: А=Д, В=С.
2.Диагонали равны: АС=ВД.
Прямоугольной трапецией называется трапеция, у которой одна из боковых сторон перпендикулярна к основанию.
Д
С
В
А
Н
М
2