Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по геометрии "Расстояние между скрещивающимися прямыми. Решение задач" 10 класс
Содержание
- 1. Презентация по геометрии "Расстояние между скрещивающимися прямыми. Решение задач" 10 класс
- 2. Методы нахождения расстояний между скрещивающимися прямыми.
- 3. Методы нахождения расстояний между скрещивающимися прямыми.Определение 1:
- 4. Методы нахождения расстояний между скрещивающимися прямыми.Определение 1:
- 5. Методы нахождения расстояний между скрещивающимися прямыми.
- 6. Методы нахождения расстояний между скрещивающимися прямыми.Решение (определение 3). HA1=ρ(DA1,CD1)=2
- 7. Методы нахождения расстояний между скрещивающимися прямыми.Решение (определение 4). OH=ρ(A1D,CD1)=2
- 8. Методы нахождения расстояний между скрещивающимися прямыми.Решение (метод
- 9. Методы нахождения расстояний между скрещивающимися прямыми.Решение (определение 3). HA1=ρ(DA1,CD1)=2
- 10. Методы нахождения расстояний между скрещивающимися прямыми.Решение (метод ортогонального проектирования).FH=ρ(DA1,CD1)=2
- 11. Методы нахождения расстояний между скрещивающимися прямыми.Решение (метод
- 12. Методы нахождения расстояний между скрещивающимися прямыми.Решение (определение 3). HA1=ρ(DA1,CD1)=2
- 13. 4 В правильной треугольной пирамиде
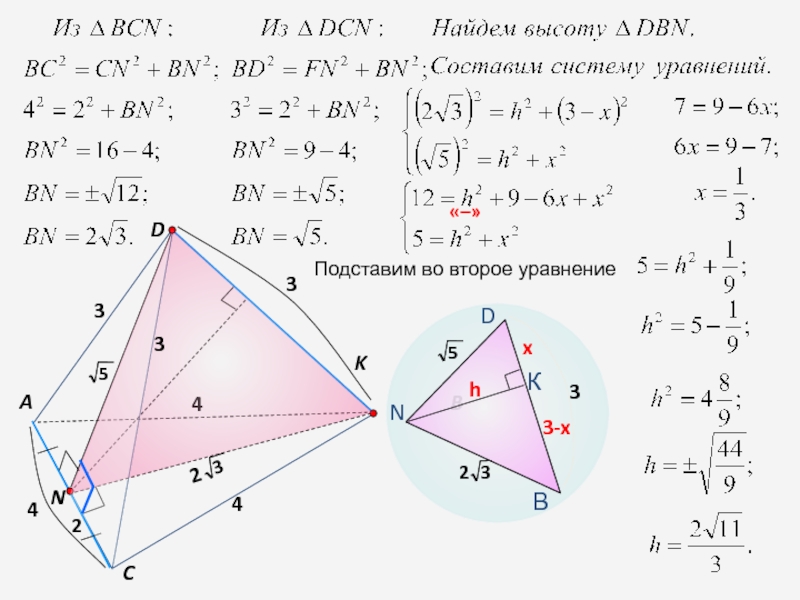
- 14. DBAC3434432hx3-x«–»Подставим во второе уравнение
- 15. Слайд 15
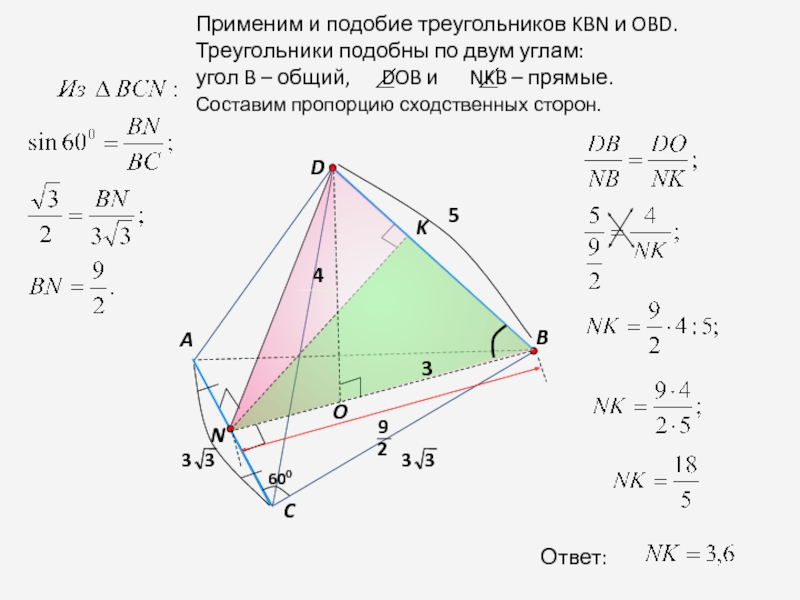
- 16. DBACСоставим пропорцию сходственных сторон. Ответ:3
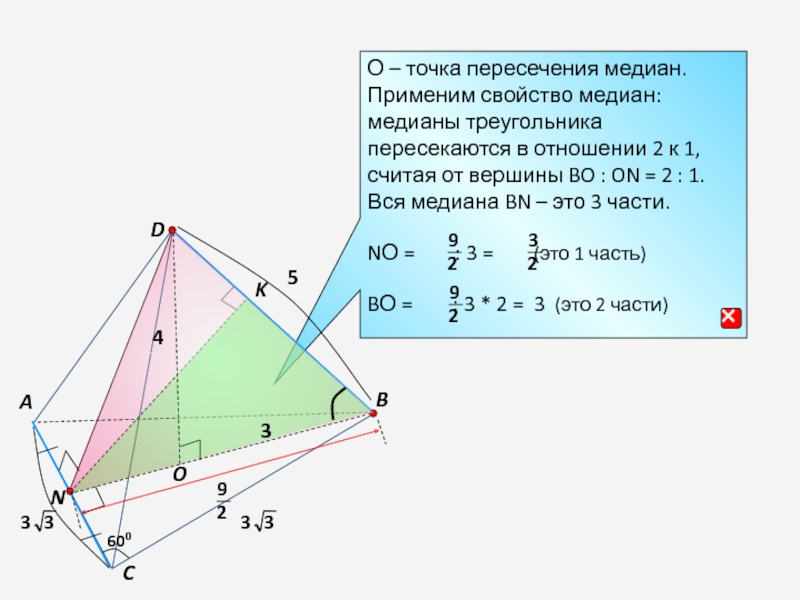
- 17. DBAC3
- 18. Скачать презентанцию
Слайды и текст этой презентации
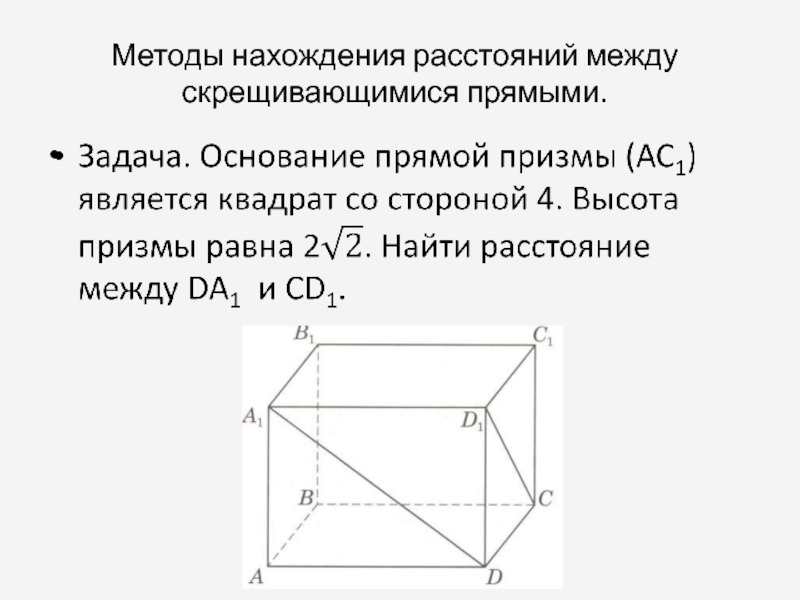
Слайд 1Занятие по геометрии в 10 классе по теме: «Расстояние между скрещивающимися
прямыми. Решение задач»
Слайд 3Методы нахождения расстояний между скрещивающимися прямыми.
Определение 1: Расстоянием между скрещивающимися
прямыми называется расстояние между ближайшими точками этих прямых.
Определение2: Расстояние между
скрещивающимися прямыми называется длина их общего перпендикуляра.Определение 3: …называется расстояние от одной из скрещивающихся прямых до параллельной плоскости, проходящей через другую прямую.
Определение 4: … называется расстояние между параллельными плоскостями, в которых находятся скрещивающиеся прямые.
Определение 5: … называется расстояние между из проекциями на плоскость, перпендикулярную одной из этих прямых.
Слайд 4Методы нахождения расстояний между скрещивающимися прямыми.
Определение 1: Расстоянием между скрещивающимися
прямыми называется расстояние между ближайшими точками этих прямых.
Определение2: Расстояние между
скрещивающимися прямыми называется длина их общего перпендикуляра.Определение 3: …называется расстояние от одной из скрещивающихся прямых до параллельной плоскости, проходящей через другую прямую.
Определение 4: … называется расстояние между параллельными плоскостями, в которых находятся скрещивающиеся прямые.
Определение 5: … называется расстояние между из проекциями на плоскость, перпендикулярную одной из этих прямых.
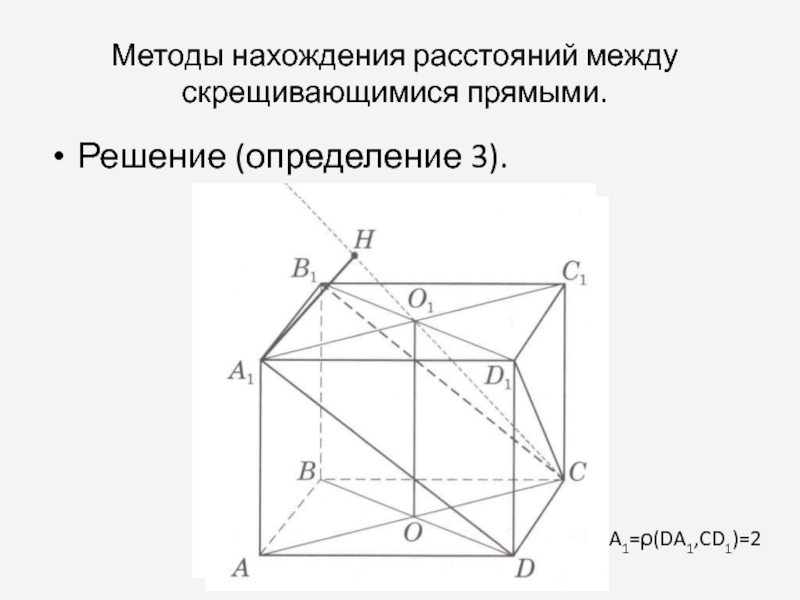
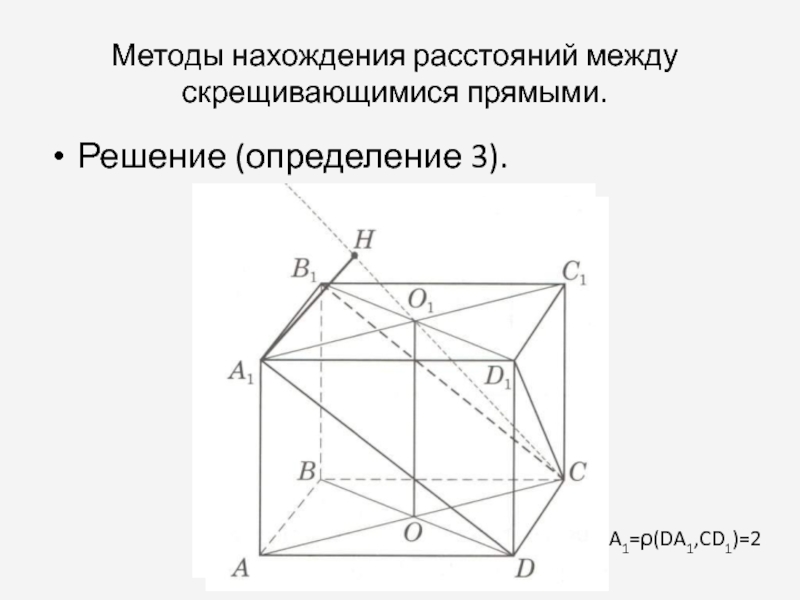
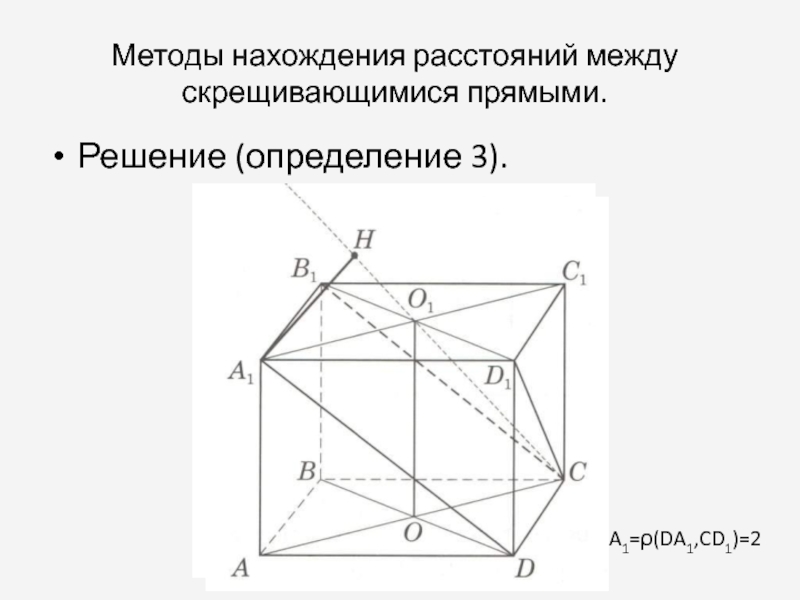
Слайд 6Методы нахождения расстояний между скрещивающимися прямыми.
Решение (определение 3).
HA1=ρ(DA1,CD1)=2
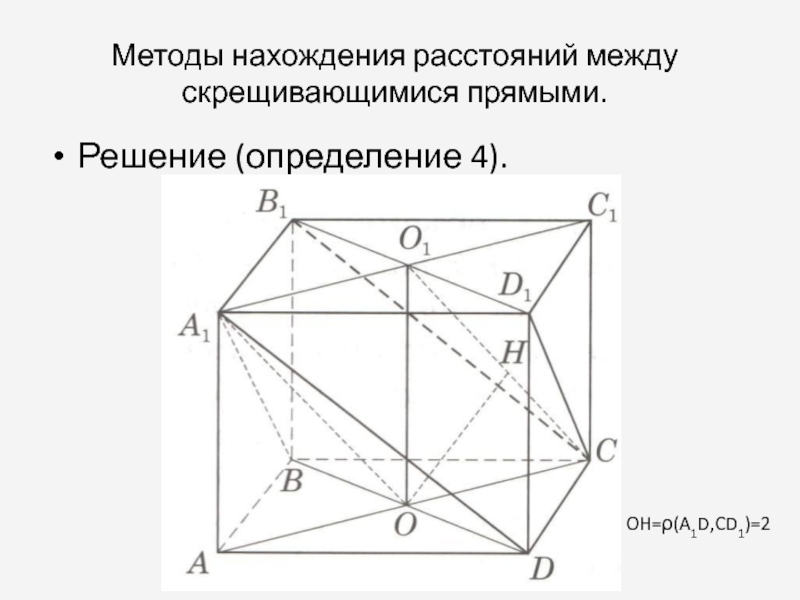
Слайд 7Методы нахождения расстояний между скрещивающимися прямыми.
Решение (определение 4).
OH=ρ(A1D,CD1)=2
Слайд 8Методы нахождения расстояний между скрещивающимися прямыми.
Решение (метод объемов).
Используют вспомогательную
пирамиду, высота которой есть искомое расстояние между двумя скрещивающимися прямыми.
Для
её нахождения вычисляют объем этой пирамиды двумя способами, и затем находят высоту.Слайд 9Методы нахождения расстояний между скрещивающимися прямыми.
Решение (определение 3).
HA1=ρ(DA1,CD1)=2
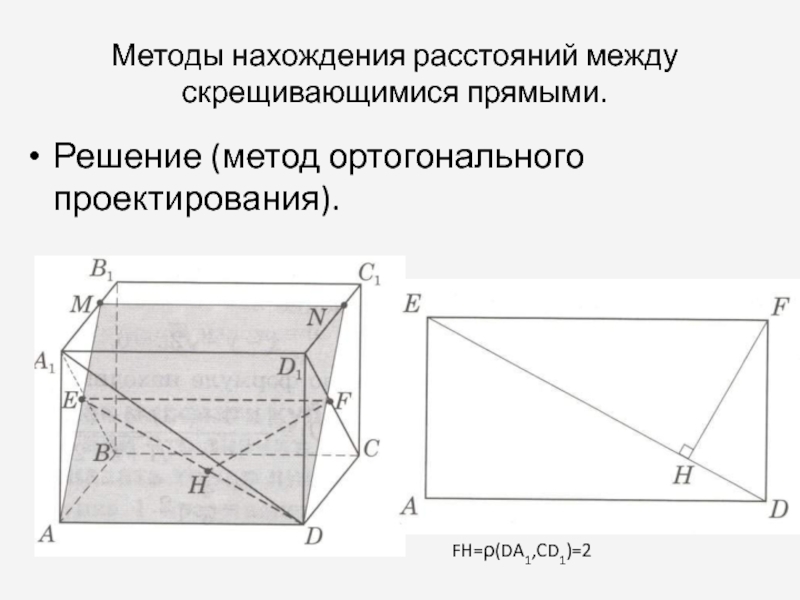
Слайд 10Методы нахождения расстояний между скрещивающимися прямыми.
Решение (метод ортогонального проектирования).
FH=ρ(DA1,CD1)=2
Слайд 11Методы нахождения расстояний между скрещивающимися прямыми.
Решение (метод координат).
Уравнение плоскости ax+by+cz+d=0,
Проходящей
через точки A1,B,D.
Решаем систему относительно a,b,c,d:
(A1)
(B)
(D)
ρ(DA1,CD1) = 2
Слайд 12Методы нахождения расстояний между скрещивающимися прямыми.
Решение (определение 3).
HA1=ρ(DA1,CD1)=2
Слайд 134
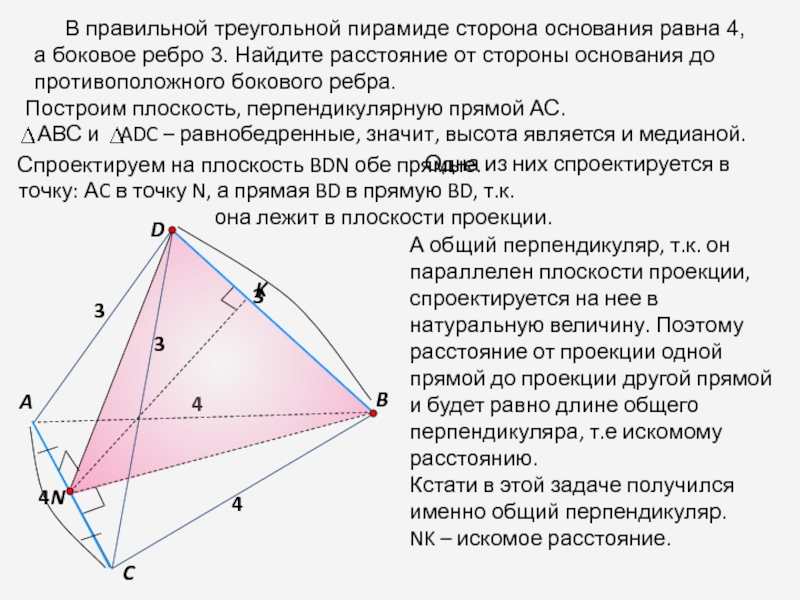
В правильной треугольной пирамиде сторона основания равна
4, а боковое ребро 3. Найдите расстояние от стороны основания
до противоположного бокового ребра.D
B
A
C
3
4
3
Построим плоскость, перпендикулярную прямой АС.
Спроектируем на плоскость BDN обе прямые.
Одна из них спроектируется в точку: АC в точку N, а прямая BD в прямую BD, т.к.
она лежит в плоскости проекции.
А общий перпендикуляр, т.к. он параллелен плоскости проекции, спроектируется на нее в натуральную величину. Поэтому расстояние от проекции одной прямой до проекции другой прямой и будет равно длине общего перпендикуляра, т.е искомому расстоянию.
Кстати в этой задаче получился именно общий перпендикуляр.
NK – искомое расстояние.
4
3
Слайд 15
Одна из них
спроектируется в точку: АC в точку N,
а прямая BD в прямую BD, т.к. она лежит
в плоскости проекции.
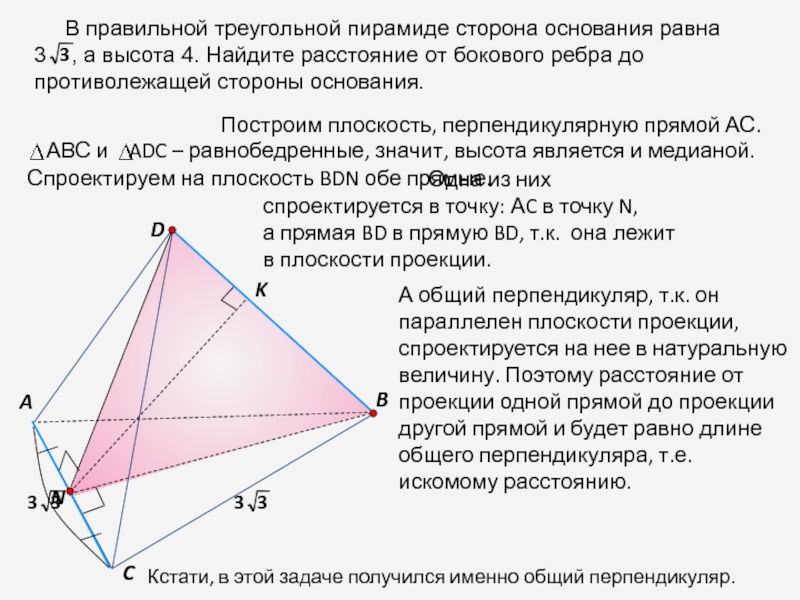
В правильной треугольной пирамиде сторона основания равна
3 , а высота 4. Найдите расстояние от бокового ребра до противолежащей стороны основания.
D
B
A
C
Построим плоскость, перпендикулярную прямой АС.
Спроектируем на плоскость BDN обе прямые.
А общий перпендикуляр, т.к. он параллелен плоскости проекции, спроектируется на нее в натуральную величину. Поэтому расстояние от проекции одной прямой до проекции другой прямой и будет равно длине общего перпендикуляра, т.е. искомому расстоянию.
Кстати, в этой задаче получился именно общий перпендикуляр.