4
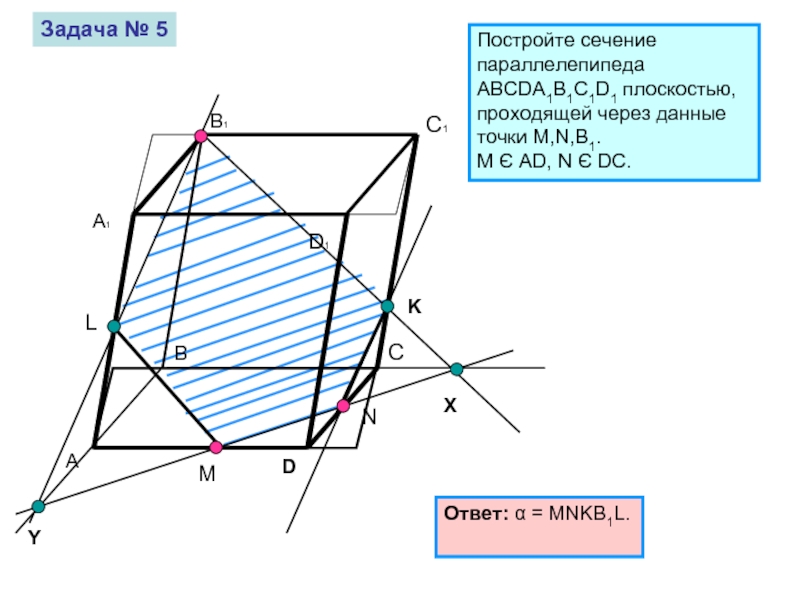
Задача № 5
Задачи для самостоятельного решения
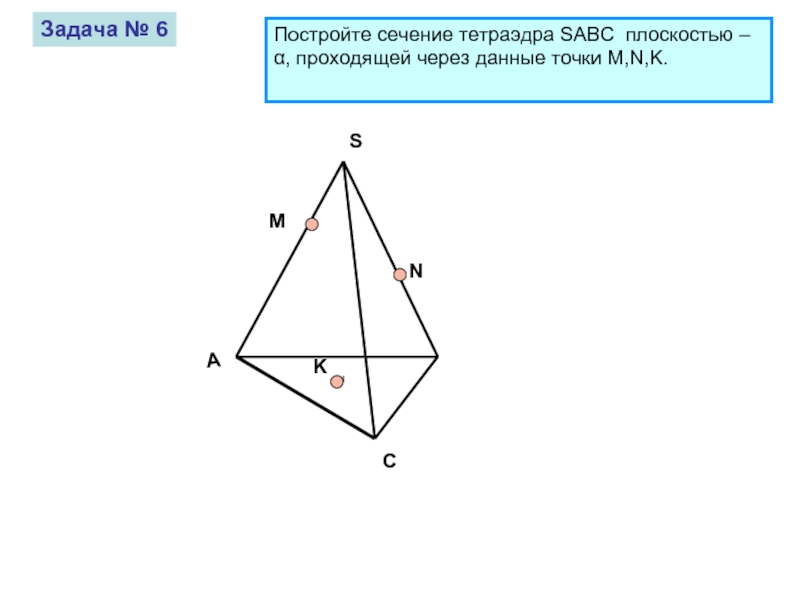
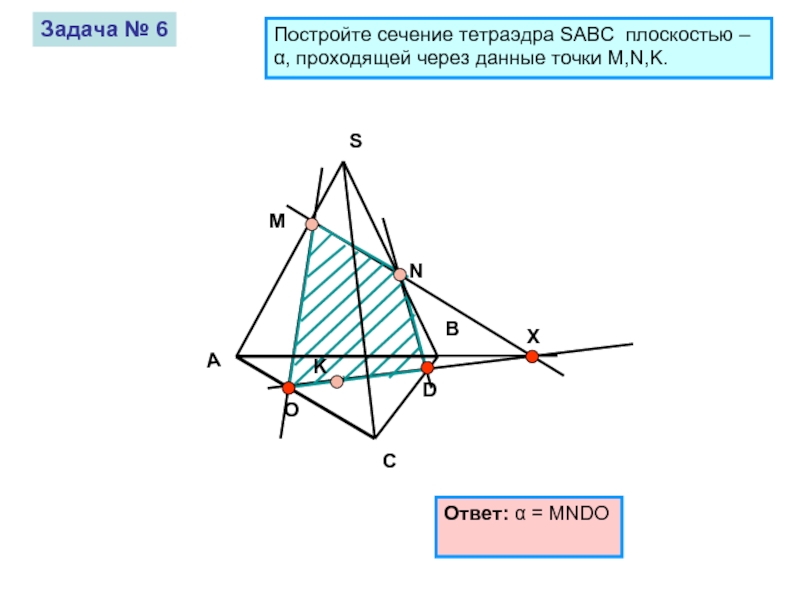
Задача № 6
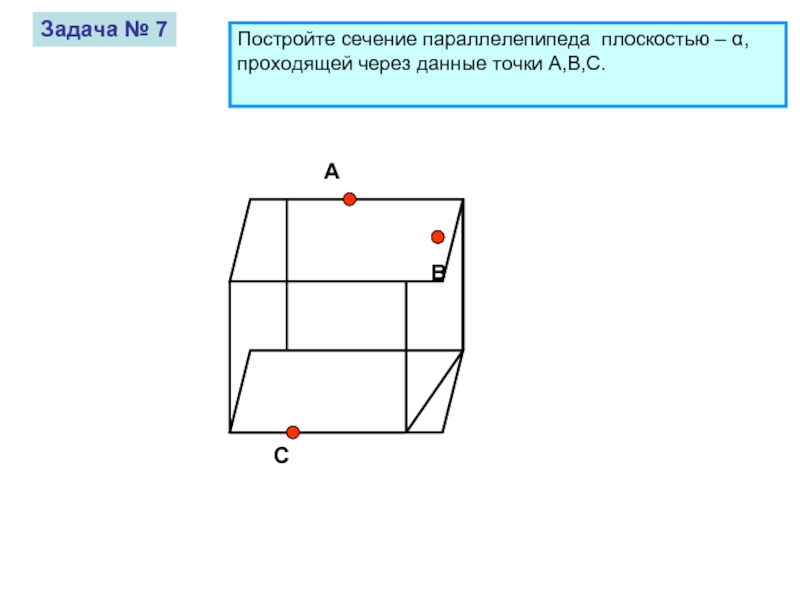
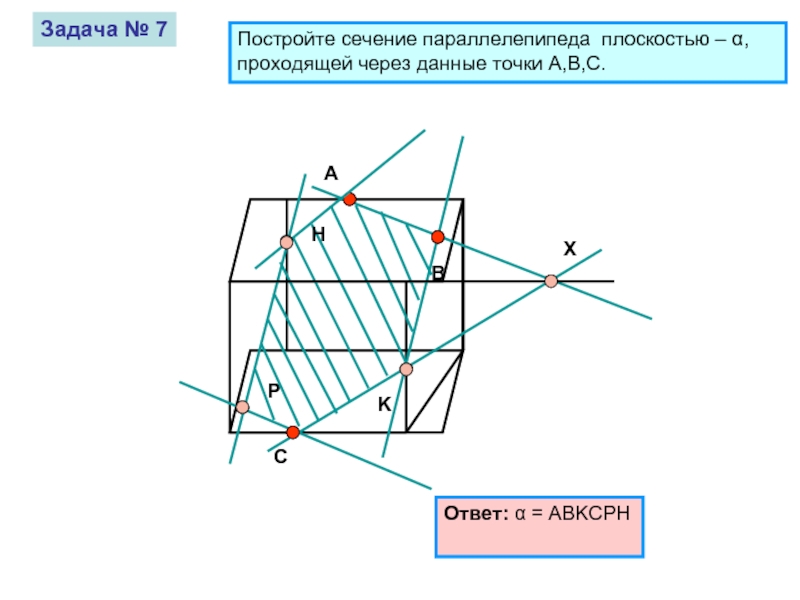
Задача № 7
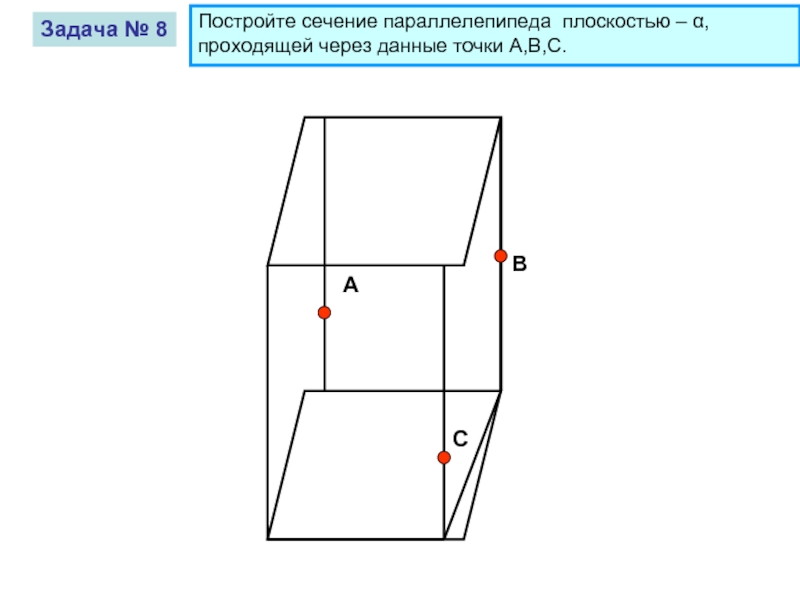
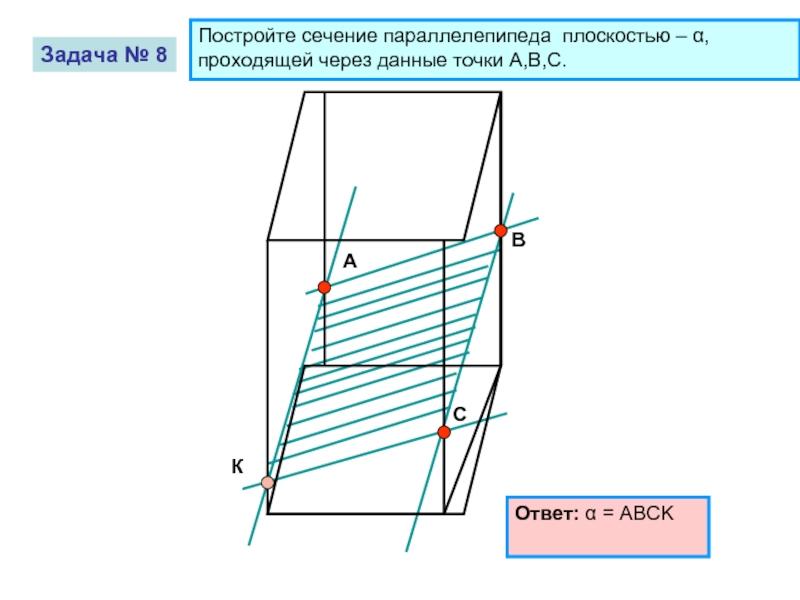
Задача № 8
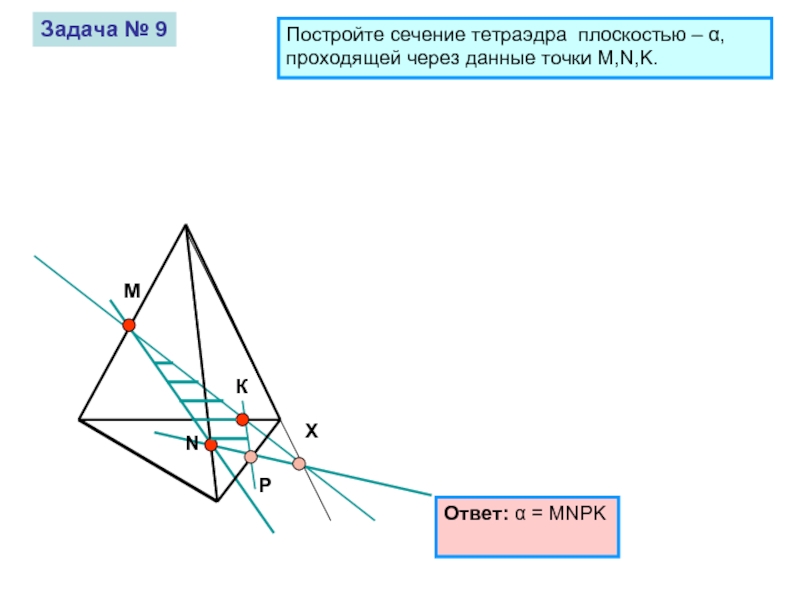
Задача № 9
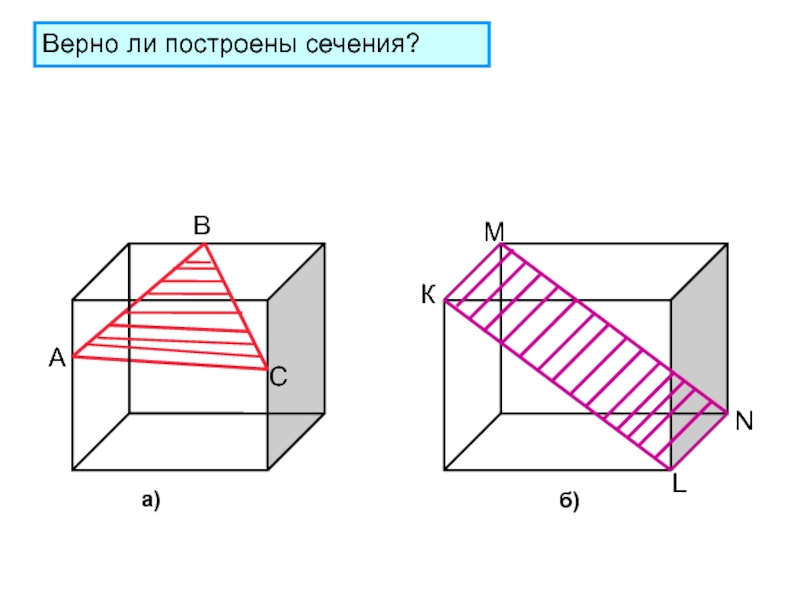
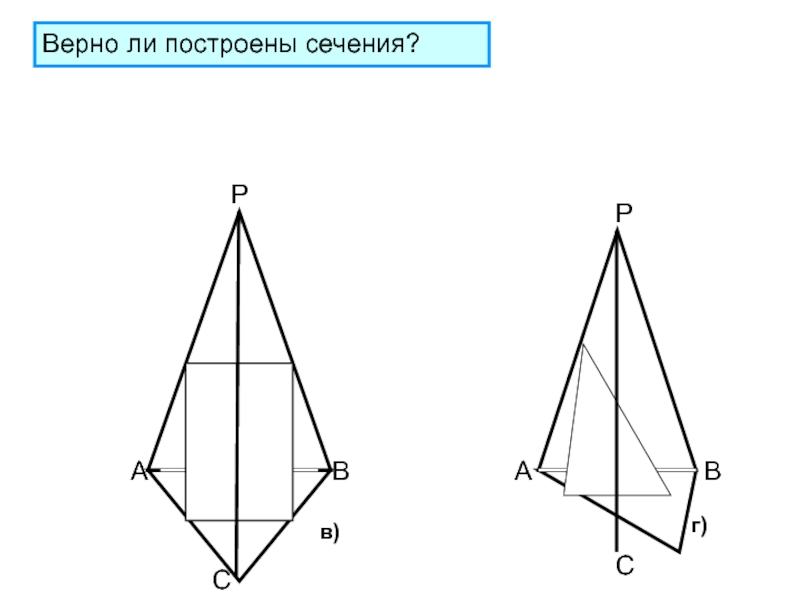
Проверка правильности решения задач
Задача № 6
Задача № 7
Задача № 8
Задача № 9