Решение стереометрических задач приподготовке к ЕГЭ

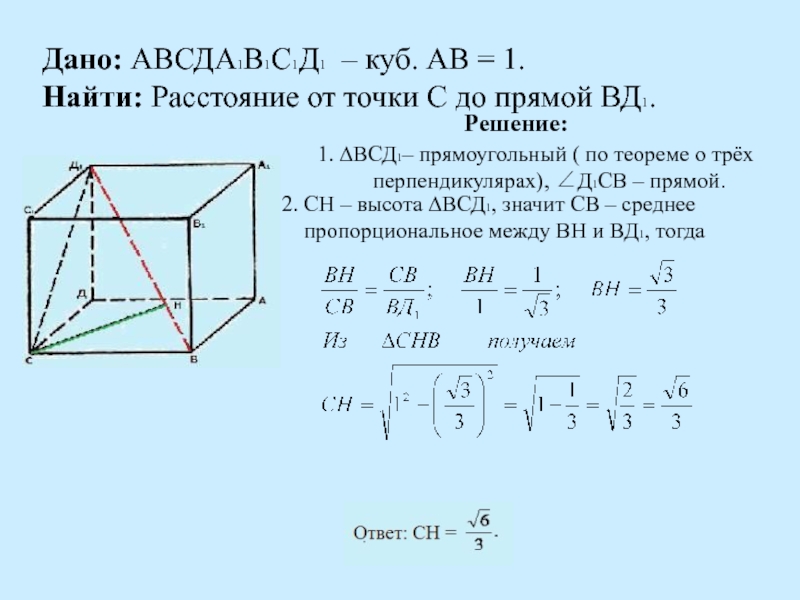
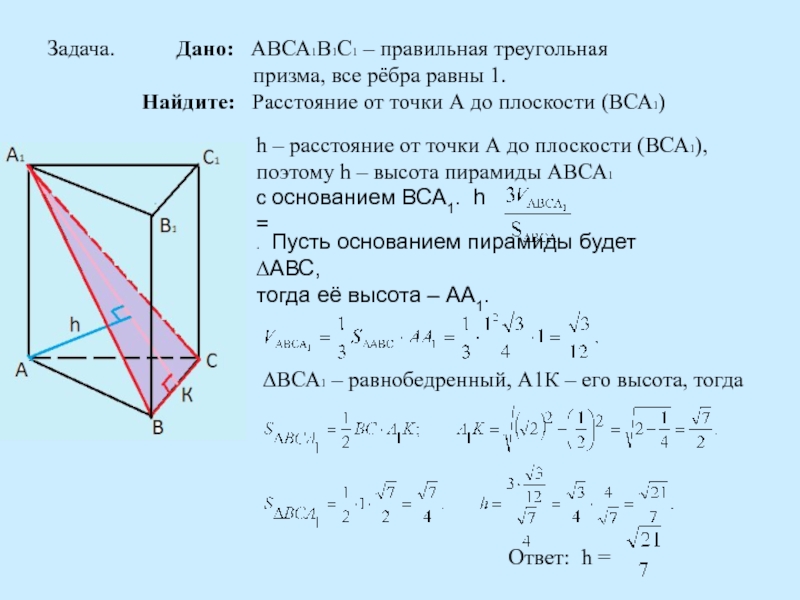
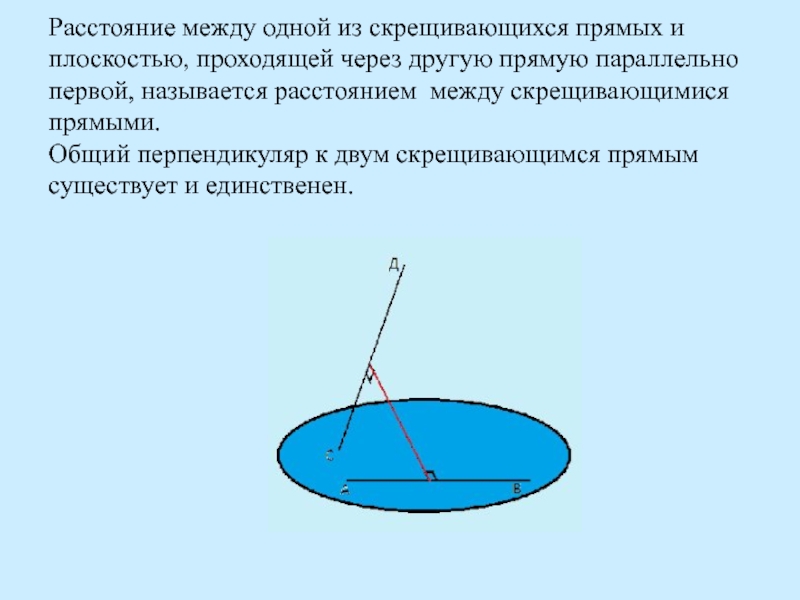
в образовательном процессе

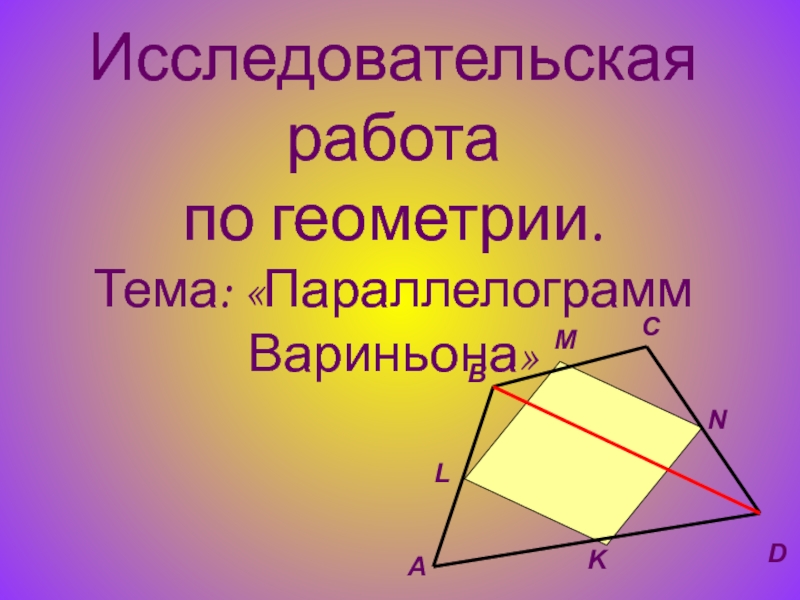
Наименование номинации 6.1: Презентация в работе с детьми

Название работы: «Решение стереометрических задач при
подготовке к ЕГЭ»
Автор: Груздева Татьяна Александровна,
учитель математики МБОУ Тонкинской СОШ,
Нижегородская область

2015 год

элективных занятиях при подготовке выпускников к сдаче ЕГЭ
Цель: Повторить

и обобщить материал по теме «Решение стереометрических задач при подготовке к ЕГЭ» и применить полученные знания в практической деятельности при решении задач.
Задачи:
Учебная: Закрепить знания и умение решать стереометрические задачи; применять ранее приобретенные знания к решению геометрических задач.
Развивающая: Развивать математическую логику, креативное мышление, пространственное воображение, навыки самостоятельной и творческой деятельности.
Воспитательная: Воспитывать интерес к предмету, точность и аккуратность в построении чертежа к геометрической задаче.

Презентация отражает следующие вопросы геометрии:
Расстояние от точки до прямой;
Расстояние от точки до плоскости;
Расстояние между двумя прямыми.

длина перпендикуляра, проведённого из данной точки к данной прямой.

С до прямой ВД1.
1. ∆ВСД1– прямоугольный ( по теореме о

трёх
перпендикулярах), ∠Д1СВ – прямой.

2. СН – высота ∆ВСД1, значит СВ – среднее
пропорциональное между ВН и ВД1, тогда

Решение:

поэтому СН – высота треугольника ВСД1. СН = 2·S∆ВСД1

: ВД1.

∆Д1СВ – прямоугольный, т.к. Д1С ⊥ СВ
по теореме о трёх перпендикулярах.

из точки А к плоскости.

правильная треугольная

призма, все рёбра равны 1. Найдите: Расстояние от точки А до плоскости (ВСА1)

h – расстояние от точки А до плоскости (ВСА1),
поэтому h – высота пирамиды АВСА1

с основанием ВСА1. h =

. Пусть основанием пирамиды будет ∆АВС,
тогда её высота – АА1.

∆ВСА1 – равнобедренный, А1К – его высота, тогда

Ответ: h =

по формуле:

, тогда


тогда

они лежат в плоскости (ВСА1).Рассмотрим
и

найдём его координаты.

другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Общий перпендикуляр

к двум скрещивающимся прямым существует и единственен.

Найдите расстояние между

прямыми АВ1 и ВС1.

следовательно расстояние между скрещивающимися
прямыми ВС1 и АВ1 равно расстоянию между
соответствующими плоскостями. Диагональ СА1
перпендикулярна этим плоскостям.
СА1 ∩ (ВДС1) = F;
CА1 ∩ (АД1В1) = Е.
EF – расстояние между ВС1 и АВ1.

В ∆ АСЕ отрезок ОF ║ АЕ и проходит через середину отрезка АС, следовательно ОF – средняя линия треугольника АСЕ и, значит, ЕF = FC. Аналогично, О1Е – средняя линия треугольника А1С1F

можно найти по формуле:

Найдите расстояние между

прямыми АВ1 и ВС1.

четырёхугольная пирамида, все

рёбра которой равны 1. Найдите: Расстояние между прямыми АS и ВС.

и профильный уровни. Авторы: Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Л.С.Киселева, Э.Г.Позняк

Москва «Просвещение» 2013 год
Избранные вопросы профильного и предпрофильного курса математики. Авторы: И.Г.Малышев, М.А. Минчасова, Б.Н.Иванов. Нижний Новгород Нижегородский гуманитарный центр, 2007 год
ЕГЭ 2011 Математика Задача С2 Геометрия Стереометрия Под редакцией А.Л.Семенова и И.В.Ященко Москва Издательство МЦНМО 2011