Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические построения 7 класс
Содержание
- 1. Геометрические построения 7 класс
- 2. ОкружностьРадиусД и а м е т рХордаооАмNFKЗадача:
- 3. ОАВСДано: окр (О; R)АВ- хорда, С середина
- 4. ООкружность называется описанной около треугольника, если она проходит, через все его вершиныОВСОМNКSFTА
- 5. ОТеорема:Центр окружности, описанной около треугольника, является точкой
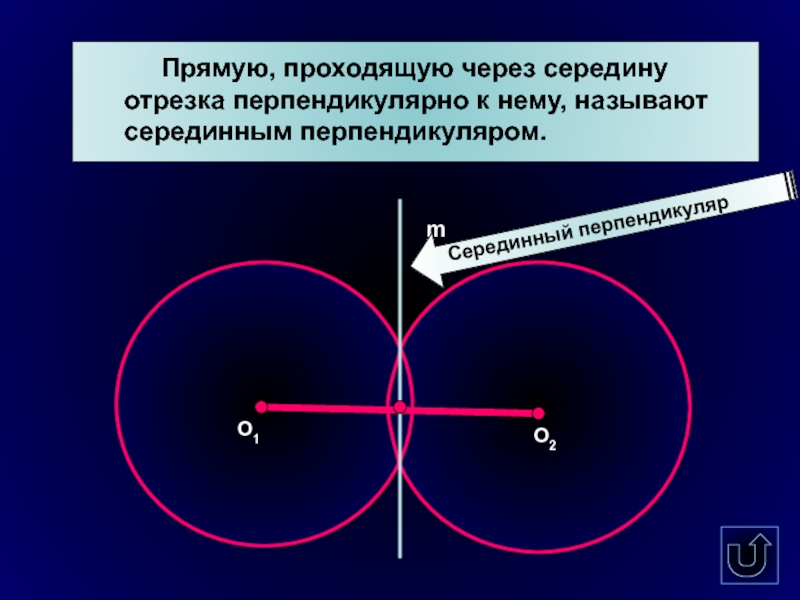
- 6. Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром.О1О2mСерединный перпендикуляр
- 7. Касательная к окружности Прямая, проходящая
- 8. Задача: Докажите, что касательная к
- 9. Окружность называется вписанной в треугольник, если она
- 10. Задачи на построение Построение треугольника с данными
- 11. Стремясь к большей точности, древние
- 12. Скачать презентанцию
ОкружностьРадиусД и а м е т рХордаооАмNFKЗадача: Докажите, что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде.
Слайды и текст этой презентации
Слайд 1Геометрические построения
Окружность
Окружность, описанная около треугольника.
Касательная к окружности.
Окружность, вписанная в треугольник.
Задачи
на построение
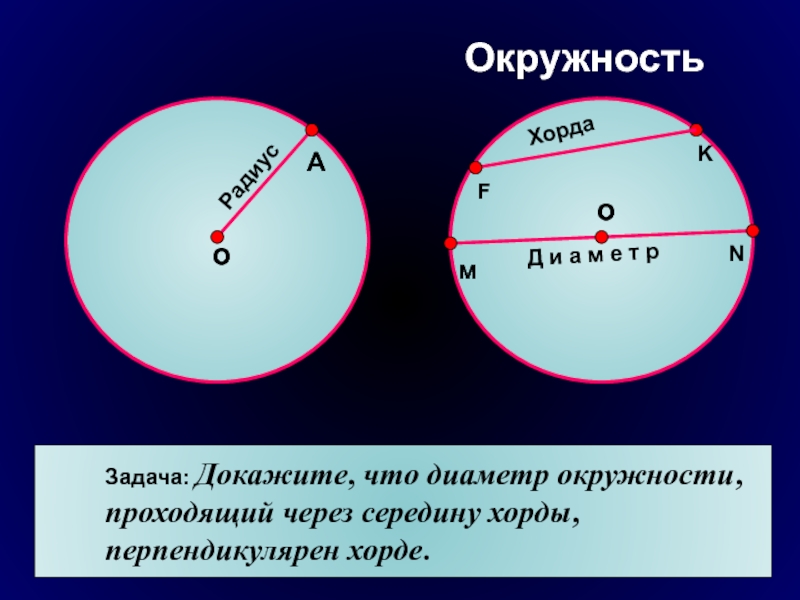
Слайд 2Окружность
Радиус
Д и а м е т р
Хорда
о
о
А
м
N
F
K
Задача: Докажите, что диаметр
окружности, проходящий через середину хорды, перпендикулярен хорде.
Слайд 3
О
А
В
С
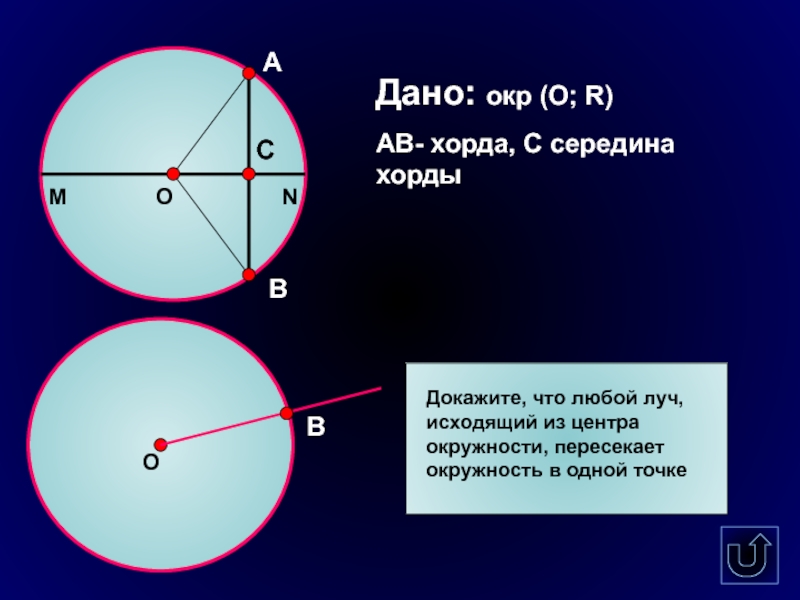
Дано: окр (О; R)
АВ- хорда, С середина хорды
M
N
О
В
Докажите, что любой
луч, исходящий из центра окружности, пересекает окружность в одной точке
Слайд 4
О
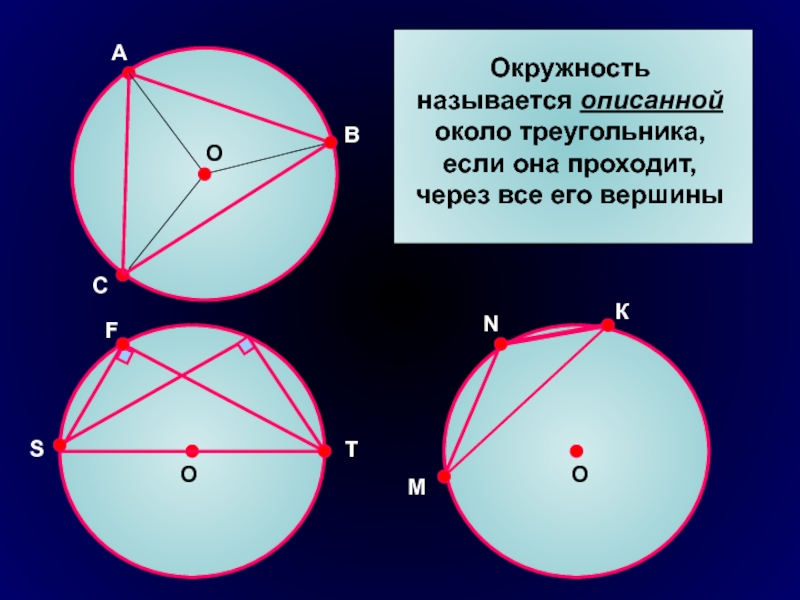
Окружность называется описанной около треугольника, если она проходит, через все
его вершины
О
В
С
О
М
N
К
S
F
T
А
Слайд 5
О
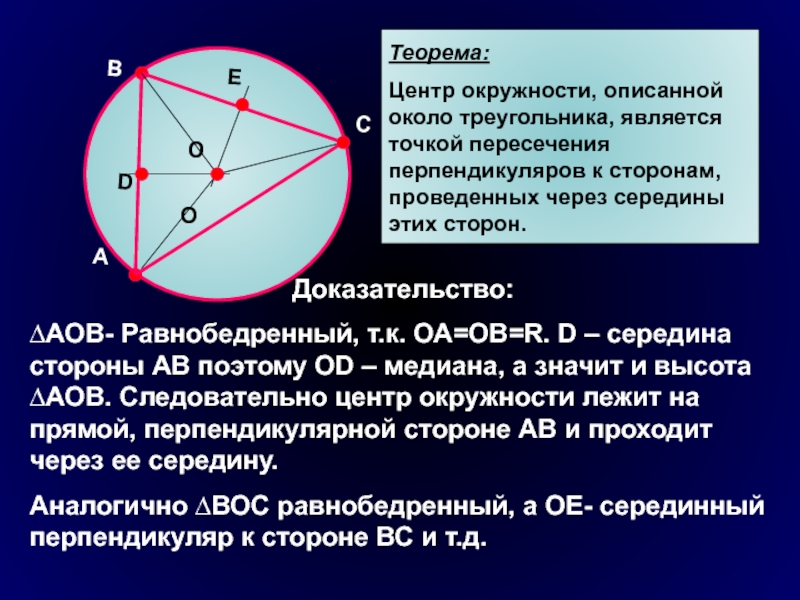
Теорема:
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к
сторонам, проведенных через середины этих сторон.
В
E C
O
D
A
Доказательство:
∆АОВ- Равнобедренный, т.к. ОА=ОВ=R. D – середина стороны АВ поэтому ОD – медиана, а значит и высота ∆АОВ. Следовательно центр окружности лежит на прямой, перпендикулярной стороне АВ и проходит через ее середину.
Аналогично ∆ВОС равнобедренный, а ОЕ- серединный перпендикуляр к стороне ВС и т.д.
Слайд 6
Прямую, проходящую через середину отрезка перпендикулярно к
нему, называют серединным перпендикуляром.
О1
О2
m
Серединный перпендикуляр
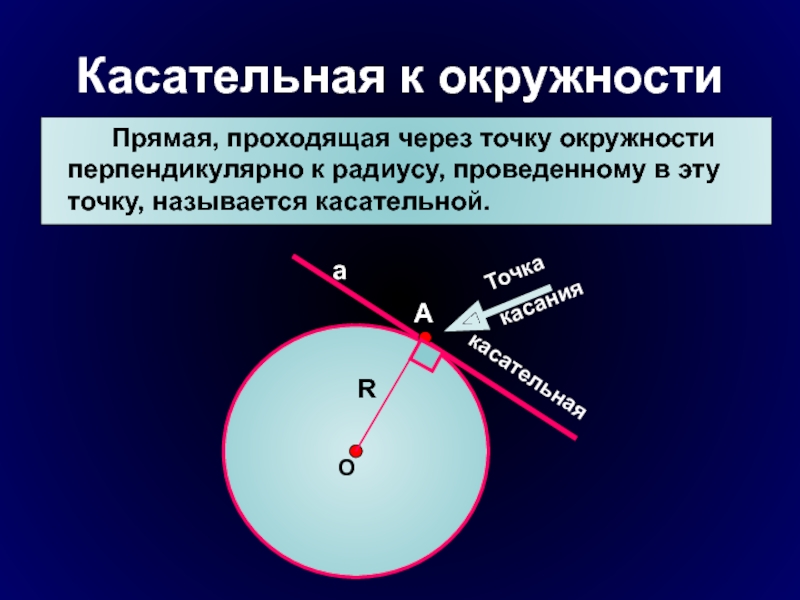
Слайд 7Касательная к окружности
Прямая, проходящая через точку окружности
перпендикулярно к радиусу, проведенному в эту точку, называется касательной.
О
А
касательная
Точка
касания
R
a
Слайд 8
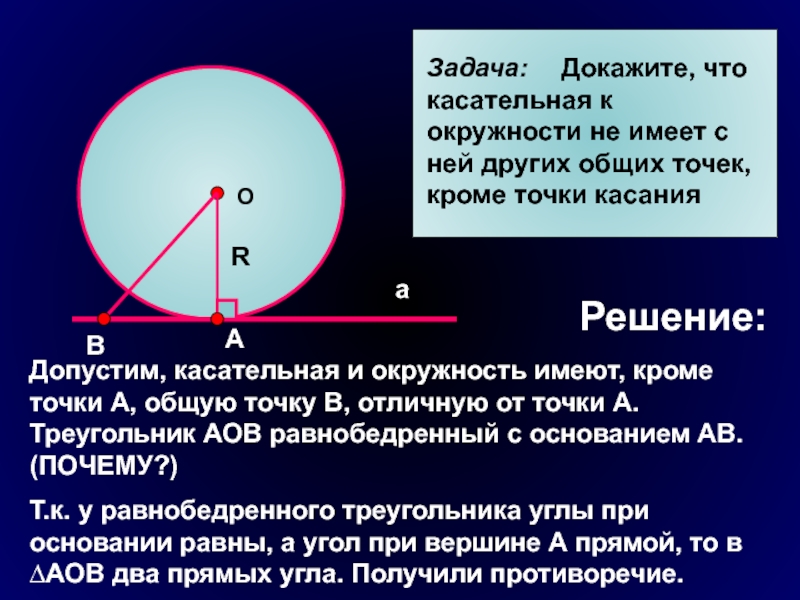
Задача: Докажите, что касательная к окружности не имеет
с ней других общих точек, кроме точки касания
О
А
R
a
В
Решение:
Допустим, касательная и
окружность имеют, кроме точки А, общую точку В, отличную от точки А. Треугольник АОВ равнобедренный с основанием АВ. (ПОЧЕМУ?)Т.к. у равнобедренного треугольника углы при основании равны, а угол при вершине А прямой, то в ∆АОВ два прямых угла. Получили противоречие.
Слайд 9
Окружность называется вписанной в треугольник, если она касается всех его
сторон
Теорема: Центр окружности, вписанной в треугольник, является
точкой пересечения его биссектрис. С
Е F
O B
D
A
Доказательство:
Пусть АВС-данный треугольник, О-центр вписанной в него окружности, D,E и F- точки касания окружности со сторонами. Прямоугольные треугольники АОD и АОЕ равны по гипотенузе и катету. У них гипотенуза АО общая, а катеты ОD и ОЕ равны как радиусы. Из равенства треугольников следует равенство углов ОАD и ОАЕ. А это значит, что точка О лежит на биссектрисе треугольника, проведенной из вершины А. Точно так же доказывается, что точка О лежит на двух других биссектрисах треугольника
Слайд 10Задачи на построение
Построение треугольника с данными сторонами
Построение треугольника
равного данному
Построение биссектрисы угла
Деление отрезка пополам
Построение перпендикулярной
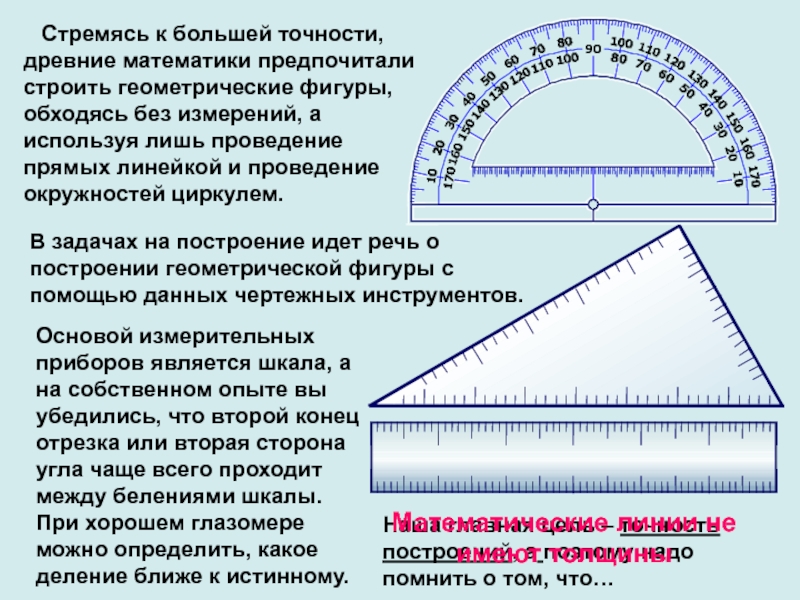
прямой
Слайд 11 Стремясь к большей точности, древние математики предпочитали строить
геометрические фигуры, обходясь без измерений, а используя лишь проведение прямых
линейкой и проведение окружностей циркулем.В задачах на построение идет речь о построении геометрической фигуры с помощью данных чертежных инструментов.
Основой измерительных приборов является шкала, а на собственном опыте вы убедились, что второй конец отрезка или вторая сторона угла чаще всего проходит между белениями шкалы. При хорошем глазомере можно определить, какое деление ближе к истинному.
Наша главная цель – точность построений, а поэтому надо помнить о том, что…
Математические линии не имеют толщины
