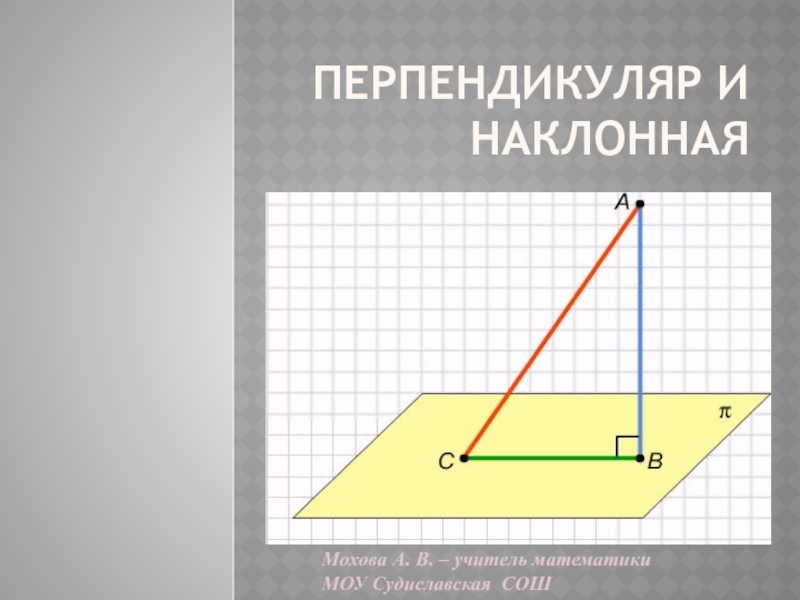
Перпендикуляр и наклонная 8 класс

Содержание

1. Перпендикуляр и наклонная 8 класс
2. Устно: Вычислить неизвестные стороны прямоугольных треугольников86?1512?54?2
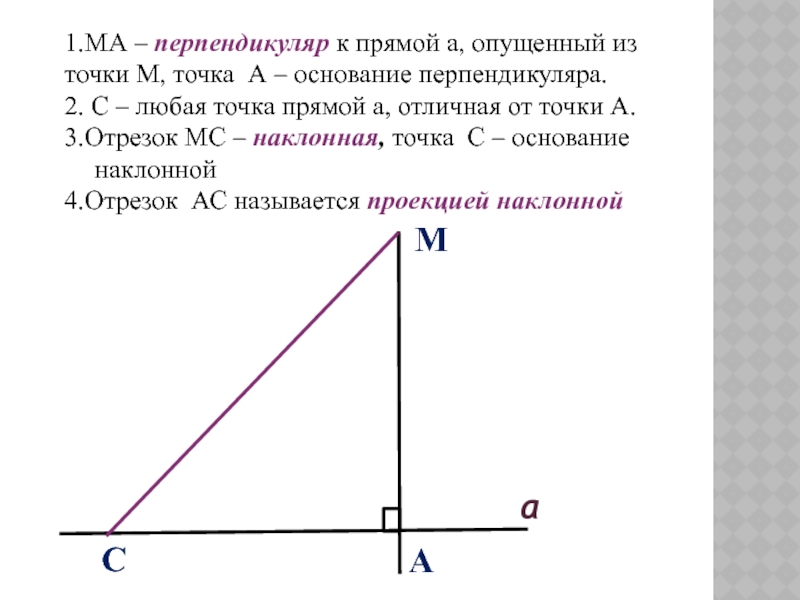
3. АСМа1.МА – перпендикуляр к прямой а, опущенный
4. УстноНазовите:а) наклонные к прямой а и их основанияб) перпендикуляры и их основанияв) проекцию каждой наклоннойаАВDМС
5. Из т. Пифагора следует, что если к
6. РЕШИТЕ ЗАДАЧУ:Дано: ОР- перпендикуляр к прямой а,
7. Решение:аРВОМСА1.Назовите проекцию наклонной ОС. Отрезок СР3.Рассмотрим Δ
8. Решите задачи:Наклонная длиной 13 см имеет проекцию
9. Рабочая тетрадь.ЗАДАЧА №132.
10. Тест1.Пусть МН – перпендикуляр ,опущенный из точки
11. Домашнее заданиеп.65 с.87, в. 6 с.93РТ №№ 129 - 131.
12. Скачать презентанцию

Устно: Вычислить неизвестные стороны прямоугольных треугольников86?1512?54?2

Главная
Геометрия
Перпендикуляр и наклонная 8 класс

Слайды и текст этой презентации

Слайд 1Перпендикуляр и наклонная
Мохова А. В. – учитель математики МОУ Судиславская

СОШ

Слайд 2Устно: Вычислить неизвестные стороны прямоугольных треугольников

8
6
?
15
12
?
5
4
?
2

Слайд 3А
С
М
а
1.МА – перпендикуляр к прямой а, опущенный из точки М,

точка А – основание перпендикуляра.
2. С – любая точка прямой

а, отличная от точки А.
3.Отрезок МС – наклонная, точка С – основание наклонной
4.Отрезок АС называется проекцией наклонной

АСМа1.МА – перпендикуляр к прямой а, опущенный из точки М, точка А – основание перпендикуляра.2. С –

Слайд 4Устно
Назовите:
а) наклонные к прямой а и их основания
б) перпендикуляры и

их основания
в) проекцию каждой наклонной
а
А
В
D
М
С

Слайд 5Из т. Пифагора следует, что если к прямой из одной

точки проведены перпендикуляр и наклонные, то
любая наклонная больше перпендикуляра,

равные наклонные имеют равные проекции,
из двух наклонных больше та, у которой проекция больше.

Из т. Пифагора следует, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая

Слайд 6РЕШИТЕ ЗАДАЧУ:
Дано: ОР- перпендикуляр к прямой а,
ОА, ОВ,ОС

и ОМ – наклонные,

проведенные к прямой а,

ОВ

ОА.

1.Сделайте рисунок
2.Запишите проекции наклоннных
в порядке возрастания их длины
3. Вычислите длину проекции наклонной ОС, если
ОС = 5см, а перпендикуляр ОР= 3см.

Слайд 7Решение:
а
Р
В
О
М
С
А
1.Назовите проекцию наклонной ОС.
Отрезок СР
3.Рассмотрим Δ ОРС – прямоугольный,

ОР и СР- катеты, ОС- гипотенуза . По теореме Пифагора:
-

Ответ: РВ, РМ, РС, РА; 4см .

Решение:аРВОМСА1.Назовите проекцию наклонной ОС. Отрезок СР3.Рассмотрим Δ ОРС – прямоугольный, ОР и СР- катеты, ОС- гипотенуза .

Слайд 8Решите задачи:
Наклонная длиной 13 см имеет проекцию 12 см. Вычислить

длину перпендикуляра.

Длина наклонной 10 см, а длина перпендикуляра 6 см.

Чему равна проекция наклонной?

Решите задачи:Наклонная длиной 13 см имеет проекцию 12 см. Вычислить длину перпендикуляра.Длина наклонной 10 см, а длина

Слайд 9Рабочая тетрадь.
ЗАДАЧА №132.

Слайд 10Тест
1.Пусть МН – перпендикуляр ,опущенный из точки М на прямую

а , А и В – любые точки прямой а.

Какое из следующих утверждений неверное ?
а) отрезок МА и МВ называются наклонными, проведенными из точки М к прямой а;
б) АН и ВН – проекции наклонных МА и МВ ;
в) если ВН < АН, то МВ < МА;
г )из данной точки , не лежащей на прямой , можно провести к этой прямой три наклонных равной длины.
2. Пусть АВ перпендикуляр, опущенный из точки А на прямую m, а АС, АР, АЕ наклонные, проведенные из точки А к прямой m. Основания этих наклонных С,Р,Е удалены от основания перпендикуляра В соответственно на
18 см,16 см и 14 см. Какая из наклонных имеет наибольшую длину?
а) АС; б) АР; в) АЕ.
3.Из точки , не лежащей на прямой , провели перпендикуляр и наклонную длиной соответственно 16 см и 20 см. Найдите проекцию наклонной.
а) 14 см; б) 12 см; в) 10 см; г ) 8 см.