Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Второй и третий признаки подобия треугольников 8 класс
Содержание
- 1. Второй и третий признаки подобия треугольников 8 класс
- 2. Вспоминаем то, что знаем
- 3. Определение подобных треугольников Первый признак подобия треугольниковОтношение площадей подобных треугольниковНачать изучение нового
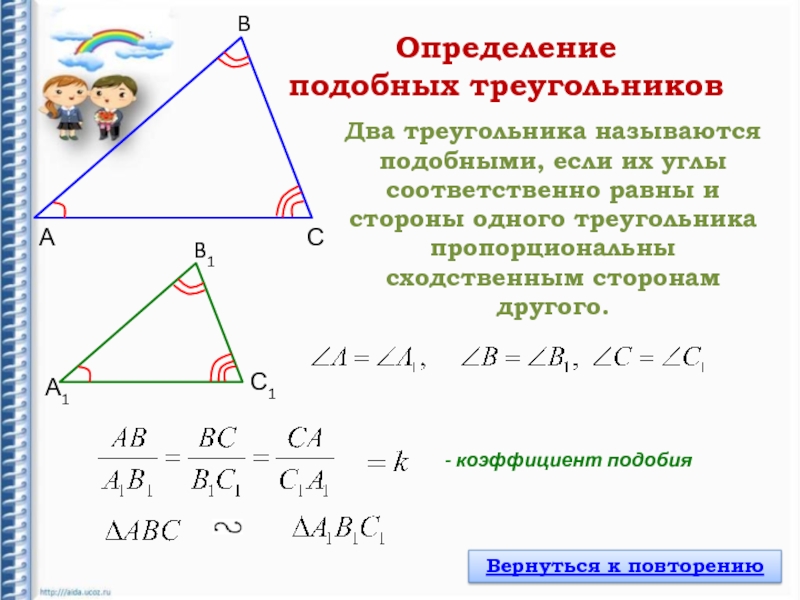
- 4. АBА1B1СС1Два треугольника называются подобными, если их углы
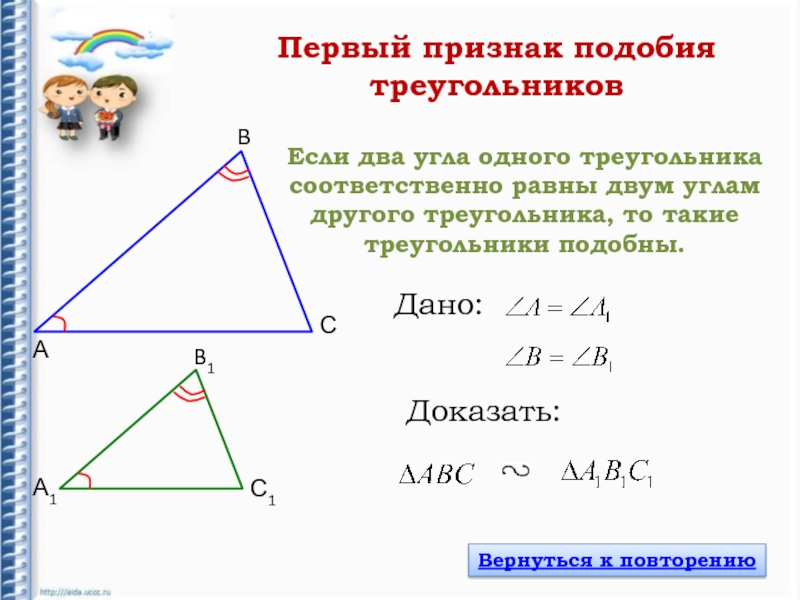
- 5. Если два угла одного треугольника соответственно равны
- 6. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.АBА1B1СС1SS1Отношение площадей подобных треугольниковВернуться к повторению
- 7. Открываем новые знания
- 8. Второй признак подобия треугольниковТретий признак подобия треугольниковНачать развивать умения
- 9. ЕСЛИ ДВЕ СТОРОНЫ ОДНОГО ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ ДВУМ
- 10. Доказательство второго признака подобия треугольниковАBА1B1СС1С212- по первому
- 11. ЕСЛИ ТРИ СТОРОНЫ ОДНОГО ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ ТРЕМ
- 12. Доказательство третьего признака подобия треугольниковАBА1B1СС1С212- по первому
- 13. Развиваем умения
- 14. Решите устно:АвСРКМ835˚35˚1045Подобны ли треугольники? Докажите.Задача №1
- 15. Решите устно:АвСРКМ25˚25˚Подобны ли треугольники? Докажите.Задача №2
- 16. Решите устно:АвСРКМ324045Подобны ли треугольники? Докажите.Задача №3243
- 17. Решите устно:АвСМ203610Подобны ли треугольники? Докажите.Задача №4189
- 18. Решите письменно:Задача № 554
- 19. Решите письменно:Задача № 554МВСАD5 cм3,6 см3,9 см8
- 20. Решите письменно:Задача № 554МВСАD5 cм3,6 см3,9 см8
- 21. Решите письменно:Задача № 554МВСАD5 cм3,6 см3,9 см8
- 22. Решите письменно:Задача № 554МВСАD5 cм3,6 см3,9 см8
- 23. Решите письменно:Задача № 554МВСАD5 cм3,6 см3,9 см8
- 24. Домашнее задание:П. 57 – 61 формулировки наизусть№ 550 № 555 (а)№ 560 (а)
- 25. Вопросы к уроку:Какие треугольники называются подобными?Чему равно отношение площадей подобных треугольников?Сформулируйте признаки подобия треугольников.
- 26. Спасибоза урок!
- 27. Скачать презентанцию
Вспоминаем то, что знаем
Слайды и текст этой презентации
Слайд 1Второй и третий признаки подобия треугольников
Презентацию подготовила Гармс Людмила Павловна
учитель
математики МБОУСОШ № 4 города Асбеста
Слайд 3Определение подобных треугольников
Первый признак подобия треугольников
Отношение площадей подобных треугольников
Начать
изучение нового
Слайд 4А
B
А1
B1
С
С1
Два треугольника называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого.
- коэффициент подобия
Определение
подобных треугольников
Вернуться к повторению
Слайд 5Если два угла одного треугольника соответственно равны двум углам другого
треугольника, то такие треугольники подобны.
А
B
А1
B1
С
С1
Первый признак подобия треугольников
Дано:
Доказать:
Вернуться к
повторению
Слайд 6Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
А
B
А1
B1
С
С1
S
S1
Отношение площадей
подобных треугольников
Вернуться к повторению
Слайд 8Второй признак подобия треугольников
Третий признак подобия треугольников
Начать развивать умения
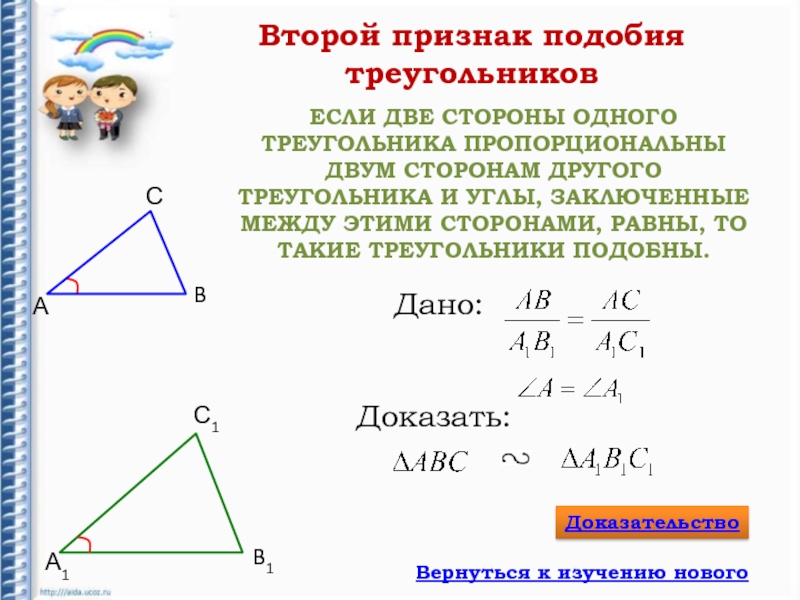
Слайд 9ЕСЛИ ДВЕ СТОРОНЫ ОДНОГО ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ ДВУМ СТОРОНАМ ДРУГОГО ТРЕУГОЛЬНИКА
И УГЛЫ, ЗАКЛЮЧЕННЫЕ МЕЖДУ ЭТИМИ СТОРОНАМИ, РАВНЫ, ТО ТАКИЕ ТРЕУГОЛЬНИКИ
ПОДОБНЫ.А
B
А1
B1
С
С1
Второй признак подобия треугольников
Дано:
Доказать:
Доказательство
Вернуться к изучению нового
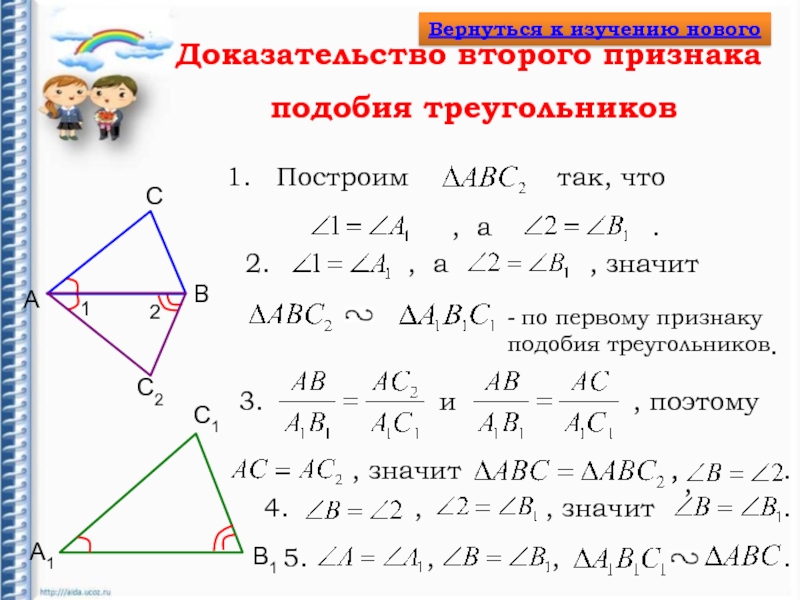
Слайд 10Доказательство второго признака
подобия треугольников
А
B
А1
B1
С
С1
С2
1
2
- по первому признаку подобия треугольников
Построим
так,
что
, а
.
, а
, значит
1.
2.
3.
, поэтому
.
, значит
и
,
4.
.
,
,
, значит
.
,
,
,
.
5.
Вернуться
к изучению нового
Слайд 11ЕСЛИ ТРИ СТОРОНЫ ОДНОГО ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ ТРЕМ СТОРОНАМ ДРУГОГО, ТО
ТАКИЕ ТРЕУГОЛЬНИКИ ПОДОБНЫ.
А
B
А1
B1
С
С1
Доказать:
Дано:
Третий признак подобия треугольников
Вернуться к изучению нового
Доказательство
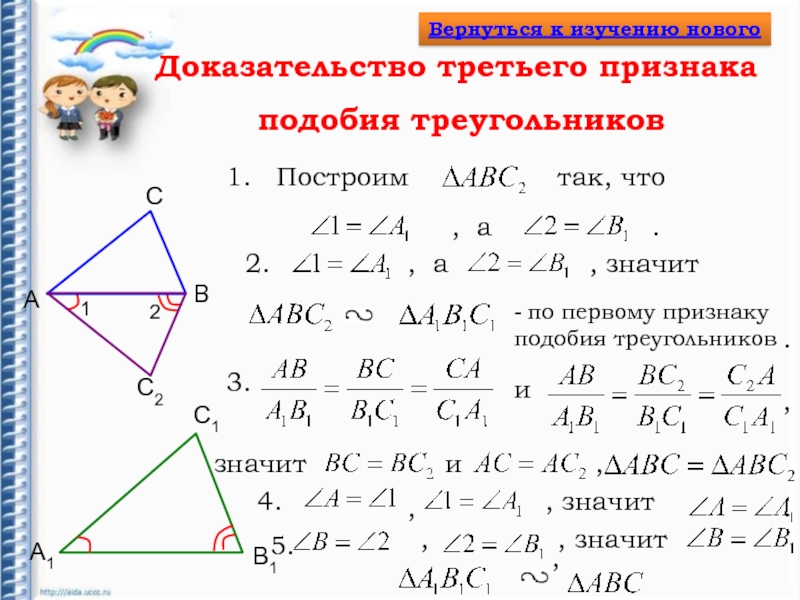
Слайд 12Доказательство третьего признака
подобия треугольников
А
B
А1
B1
С
С1
С2
1
2
- по первому признаку подобия треугольников
Построим
так,
что
, а
.
, а
, значит
1.
2.
3.
,
.
значит
и
4.
,
.
,
,
5.
Вернуться к изучению нового
и
, значит
,
, значит
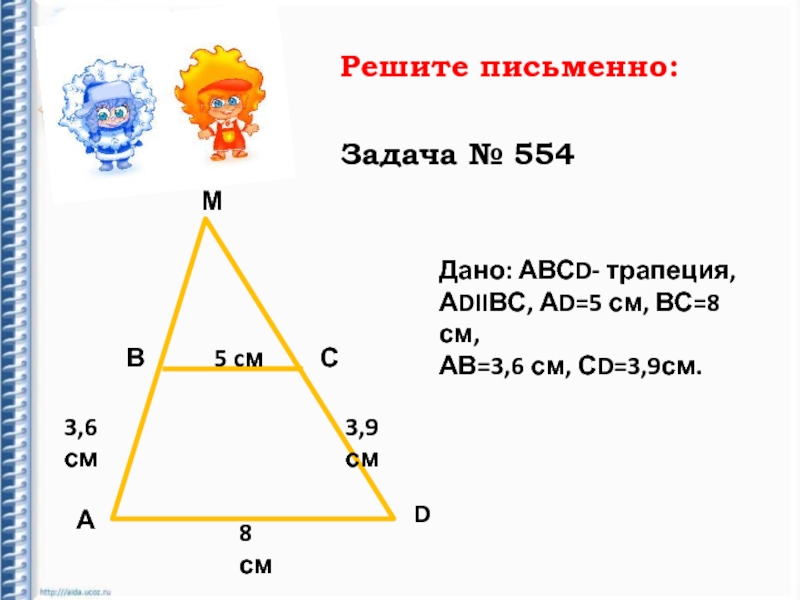
Слайд 19Решите письменно:
Задача № 554
М
В
С
А
D
5 cм
3,6 см
3,9 см
8 см
Дано: АВСD- трапеция,
АDIIВС, АD=5 см, ВС=8 см,
АВ=3,6 см, СD=3,9см.
Слайд 20Решите письменно:
Задача № 554
М
В
С
А
D
5 cм
3,6 см
3,9 см
8 см
Дано: АВСD- трапеция,
АDIIВС, АD=5 см, ВС=8 см,
АВ=3,6 см, СD=3,9см.
Найти: МВ, МС.
Решение:
Слайд 21Решите письменно:
Задача № 554
М
В
С
А
D
5 cм
3,6 см
3,9 см
8 см
Решение:
∆ АМD
∆ ВМС по первому признаку
(
общий, <В = <А , т к соответственные при пересечении параллельных прямых АD и ВС секущей АВ).2) Из подобия ∆ АМD и ∆ ВМС следует, что
АD АМ МD
ВС ВМ МС
=
=
Слайд 22Решите письменно:
Задача № 554
М
В
С
А
D
5 cм
3,6 см
3,9 см
8 см
Решение:
3) Пусть ВМ
– х см, тогда
(х + 3,6) см – АМ.
х + 3,6 8х 5
5( х + 3,6) = 8х
5х + 18 = 8х
5х – 8х = -18
-3х = -18
х = 6 (см) - МВ
х см
=
Слайд 23Решите письменно:
Задача № 554
М
В
С
А
D
5 cм
3,6 см
3,9 см
8 см
Решение:
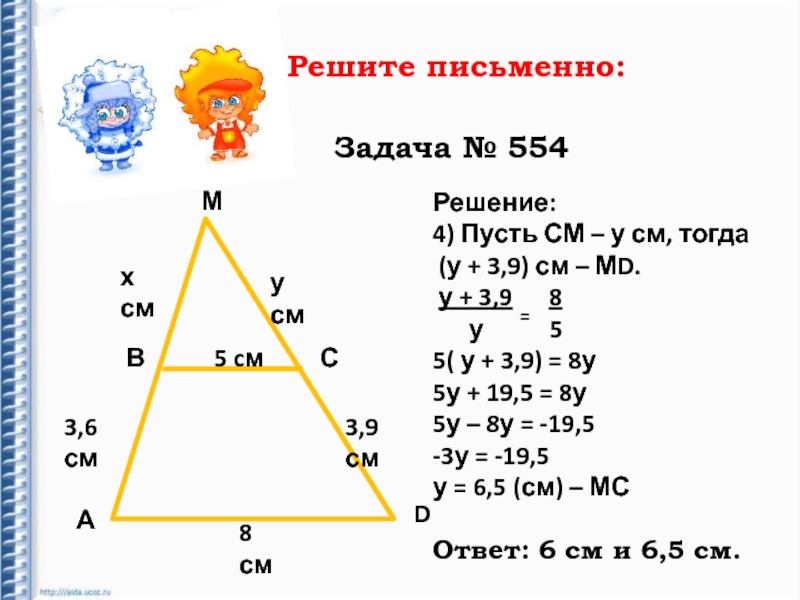
4) Пусть СМ
– у см, тогда
(у + 3,9) см – МD.
у + 3,9 8у 5
5( у + 3,9) = 8у
5у + 19,5 = 8у
5у – 8у = -19,5
-3у = -19,5
у = 6,5 (см) – МС
Ответ: 6 см и 6,5 см.
х см
=
у см
Слайд 25Вопросы к уроку:
Какие треугольники
называются подобными?
Чему равно отношение площадей
подобных
треугольников?
Сформулируйте признаки
подобия треугольников.
