Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Пифагора задачи
Содержание
- 1. Теорема Пифагора задачи
- 2. Формулировки и формулаСформулируйте и запишите с помощью
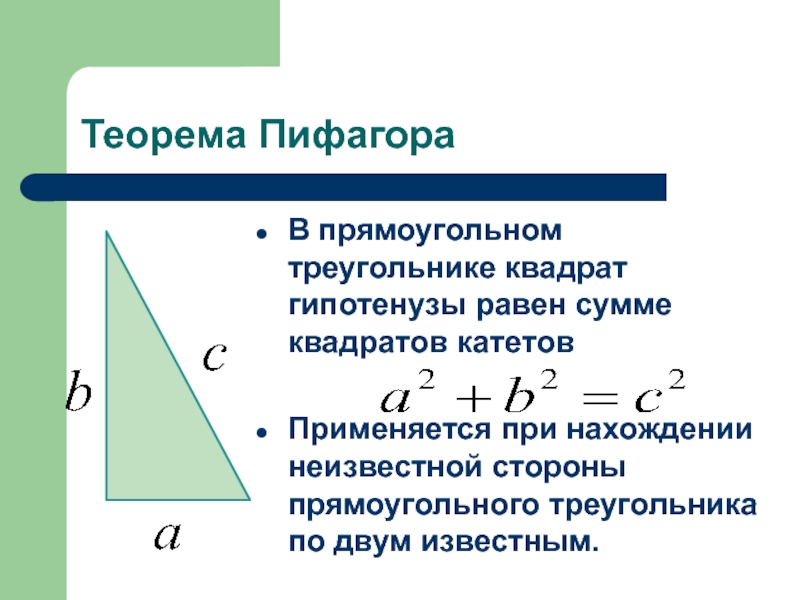
- 3. Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен
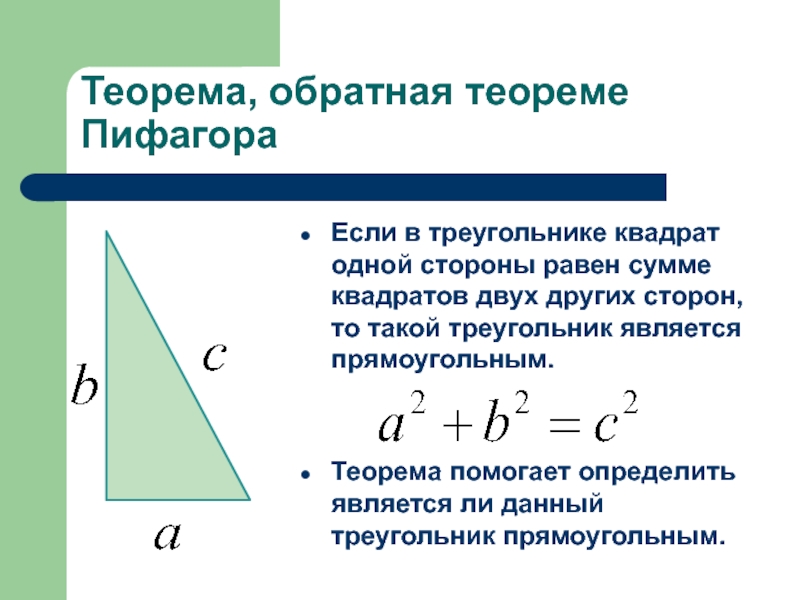
- 4. Теорема, обратная теореме ПифагораЕсли в треугольнике квадрат
- 5. Задача №1В прямоугольном треугольнике катеты равны 6 см и 8 см. Чему равна гипотенуза?
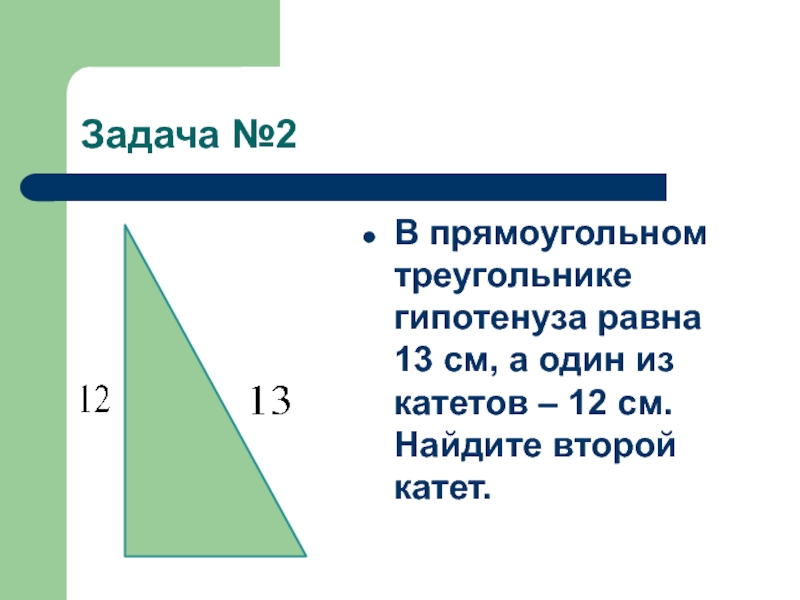
- 6. Задача №2В прямоугольном треугольнике гипотенуза равна 13
- 7. Задача №3 Определите, является ли прямоугольным треугольник со сторонами 8 м, 5 м и 9 м.
- 8. Задача №4В треугольнике две стороны равны соответственно
- 9. Задача №5Диагонали ромба равны 16 см и
- 10. Задача №6В прямоугольной трапеции большая боковая сторона
- 11. Задача №7Сторона равностороннего треугольника равна 10 см.
- 12. Скачать презентанцию
Формулировки и формулаСформулируйте и запишите с помощью букв a, b и c теорему Пифагора.Сформулируйте теорему, обратную теореме Пифагора.При решении каких задач применяются эти теоремы?
Слайды и текст этой презентации
Слайд 2Формулировки и формула
Сформулируйте и запишите с помощью букв a, b
и c теорему Пифагора.
задач применяются эти теоремы?
Слайд 3Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Применяется
при нахождении неизвестной стороны прямоугольного треугольника по двум известным.
Слайд 4Теорема, обратная теореме Пифагора
Если в треугольнике квадрат одной стороны равен
сумме квадратов двух других сторон, то такой треугольник является прямоугольным.
Теорема
помогает определить является ли данный треугольник прямоугольным.
Слайд 6Задача №2
В прямоугольном треугольнике гипотенуза равна 13 см, а один
из катетов – 12 см. Найдите второй катет.
Слайд 8Задача №4
В треугольнике две стороны равны соответственно 20 см и
15 см. Какой должна быть большая сторона, чтобы треугольник был
прямоугольным?
Слайд 9Задача №5
Диагонали ромба равны 16 см и 12 см. Вычислите:
а) сторону ромба; б) расстояние от точки пересечения диагоналей до
стороны ромба.
Слайд 10Задача №6
В прямоугольной трапеции большая боковая сторона и меньшая диагональ
равны по 13 см, а меньшее основание 12 см. Вычислите:
а) высоту трапеции; б) большую диагональ.
Слайд 11Задача №7
Сторона равностороннего треугольника равна 10 см. Найдите: а) высоту
треугольника; б) как изменится площадь этого треугольника, если его высоту
увеличить в 2 раза?
