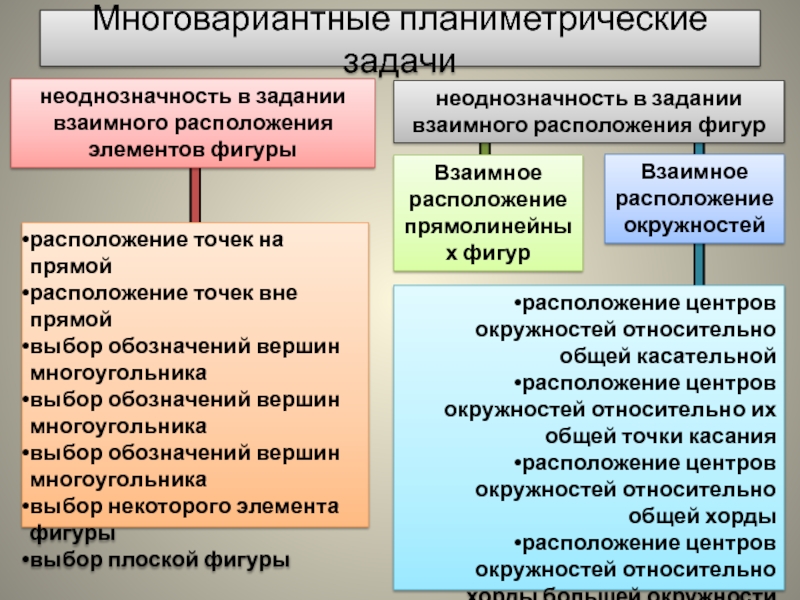
задании взаимного расположения фигур
расположение точек на прямой
расположение точек вне прямой
выбор
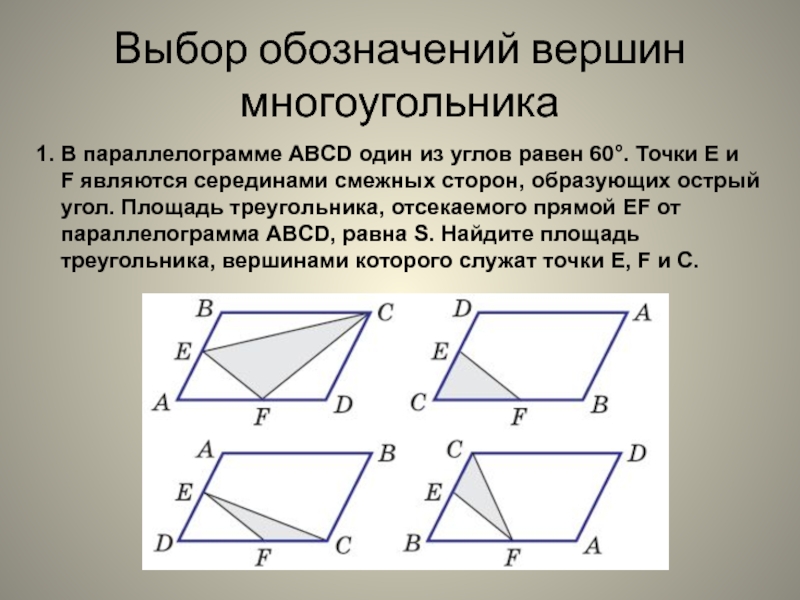
обозначений вершин многоугольникавыбор обозначений вершин многоугольника
выбор обозначений вершин многоугольника
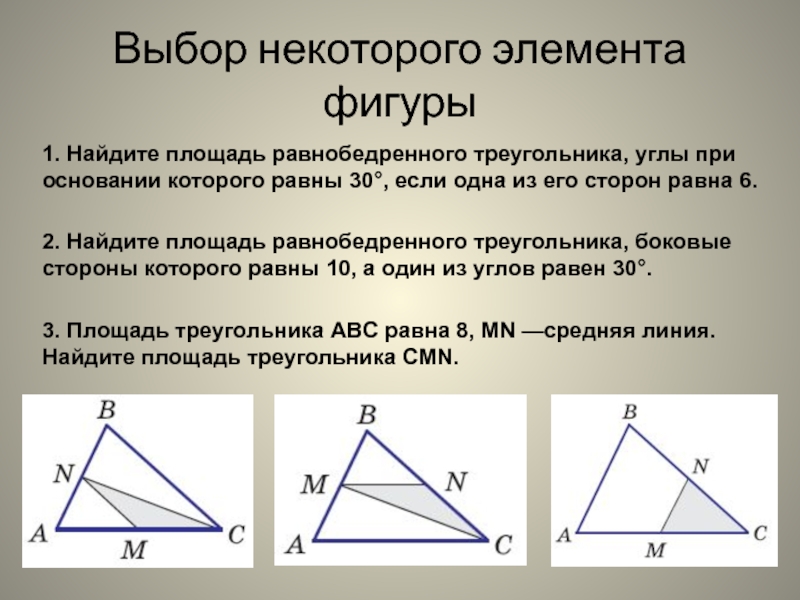
выбор некоторого элемента фигуры
выбор плоской фигуры
Взаимное расположение прямолинейных фигур
Взаимное расположение окружностей
расположение центров окружностей относительно общей касательной
расположение центров окружностей относительно их общей точки касания
расположение центров окружностей относительно общей хорды
расположение центров окружностей относительно хорды большей окружности
расположение точек касания окружности и прямой