Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное положение прямых
Содержание
- 1. Взаимное положение прямых
- 2. Взаимное расположение двух прямыхКак могут располагаться две
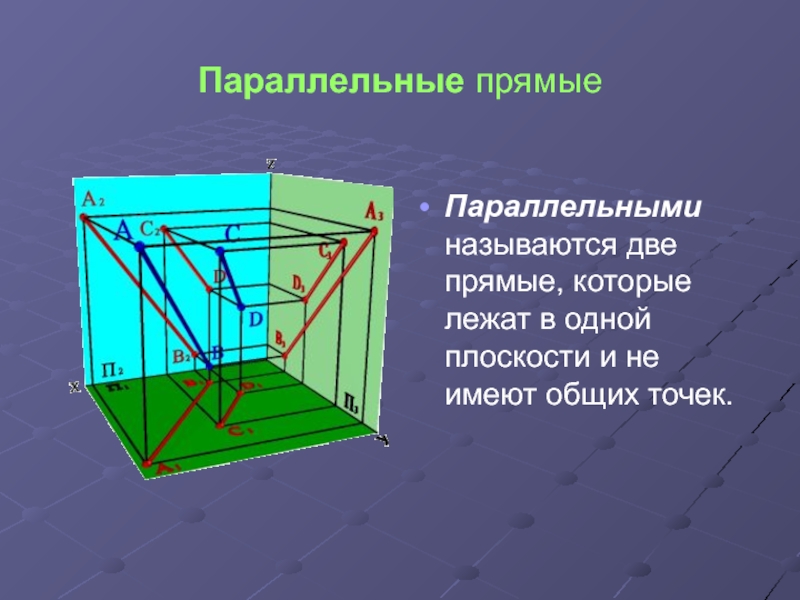
- 3. Параллельные прямые Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.
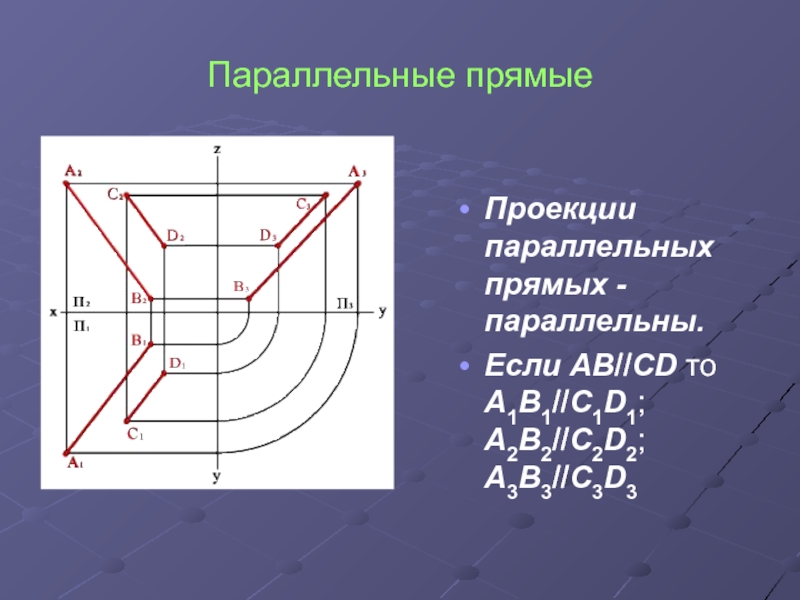
- 4. Параллельные прямые Проекции параллельных прямых - параллельны. Если ABCD то A1B1C1D1; A2B2C2D2; A3B3C3D3
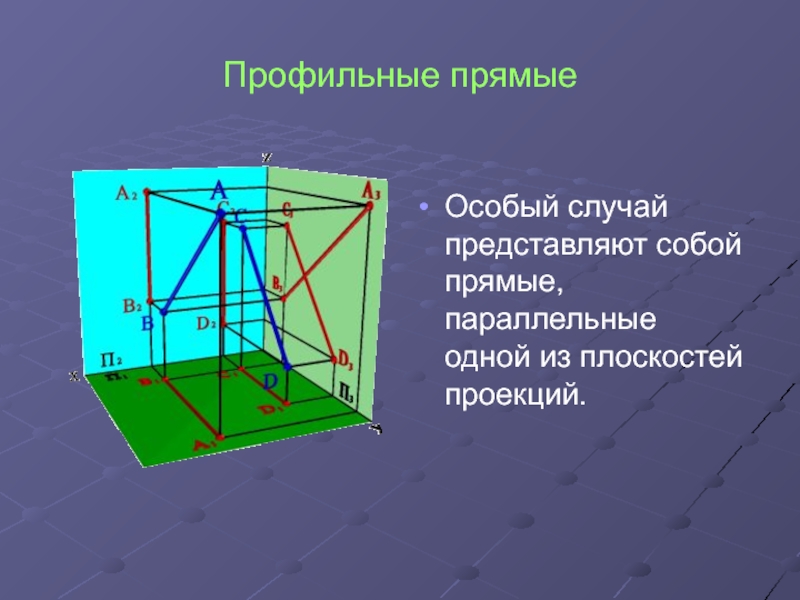
- 5. Профильные прямые Особый случай представляют собой прямые, параллельные одной из плоскостей проекций.
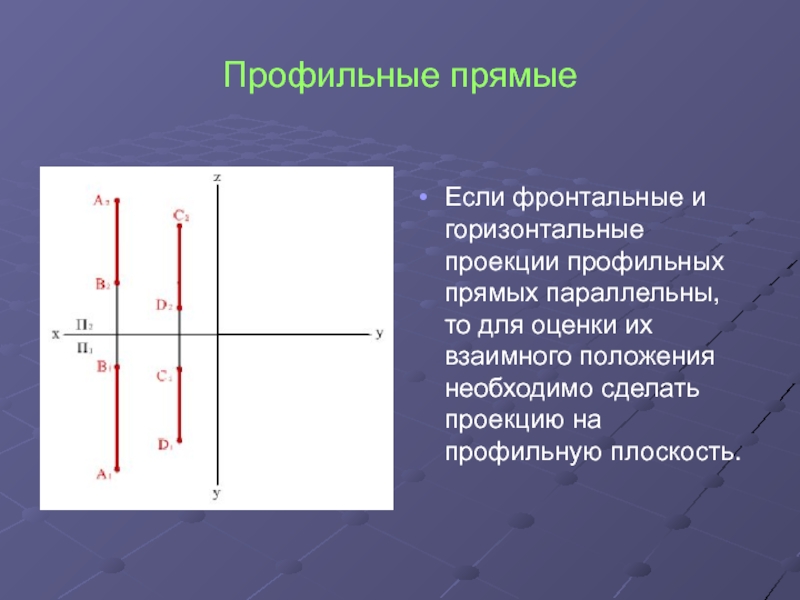
- 6. Профильные прямыеЕсли фронтальные и горизонтальные проекции профильных
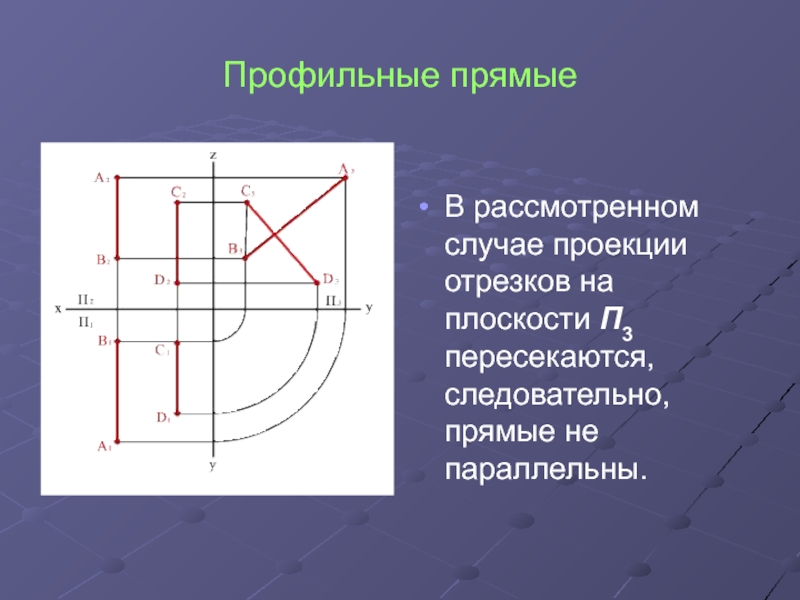
- 7. Профильные прямыеВ рассмотренном случае проекции отрезков на плоскости П3 пересекаются, следовательно, прямые не параллельны.
- 8. Пересекающиеся прямые Пересекающимися называются две прямые лежащие
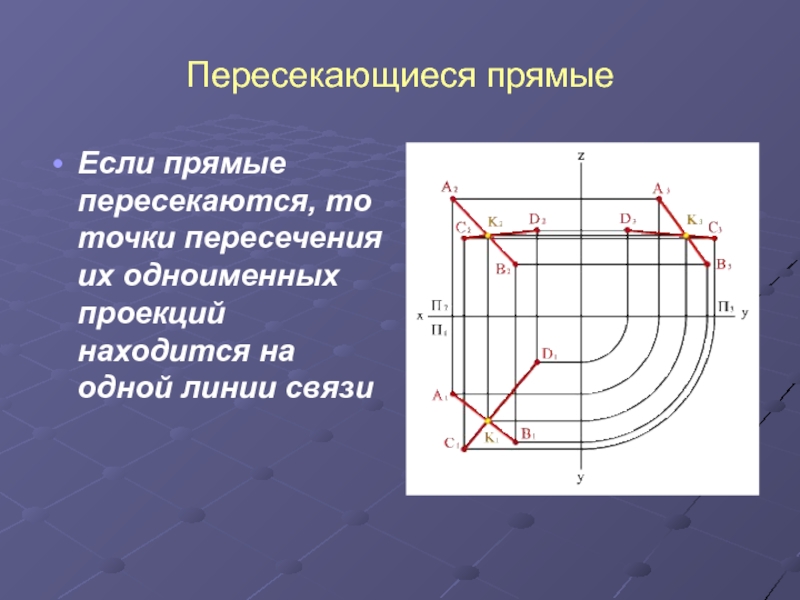
- 9. Пересекающиеся прямыеЕсли прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи
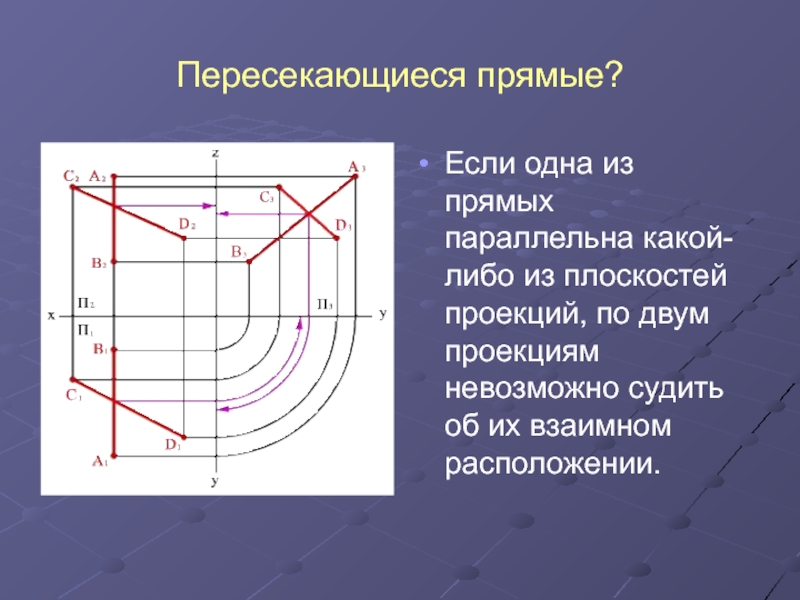
- 10. Пересекающиеся прямые?Если одна из прямых параллельна какой-либо
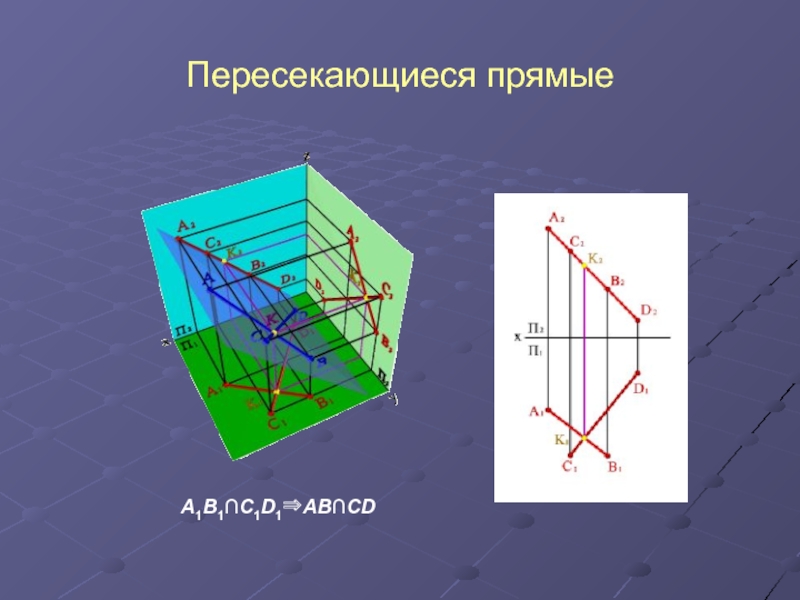
- 11. Пересекающиеся прямые А1В1∩С1D1АВ∩СD
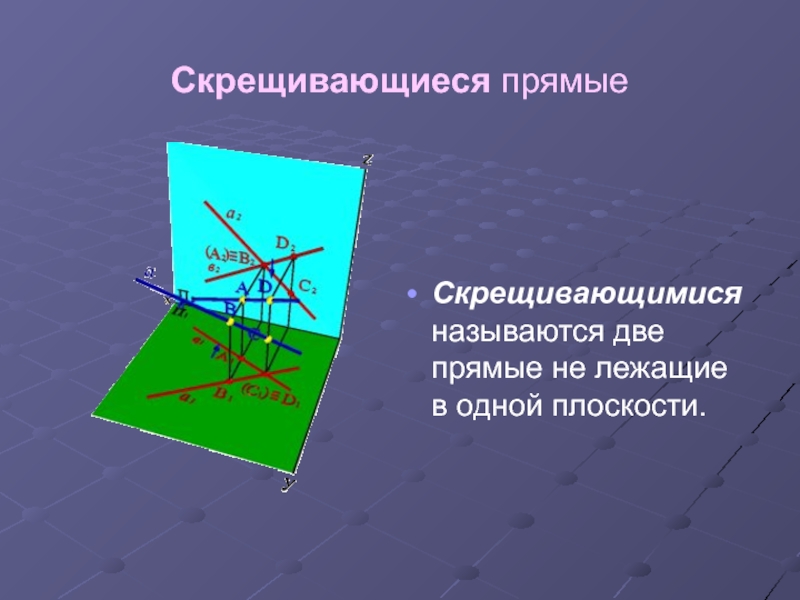
- 12. Скрещивающиеся прямые Скрещивающимися называются две прямые не лежащие в одной плоскости.
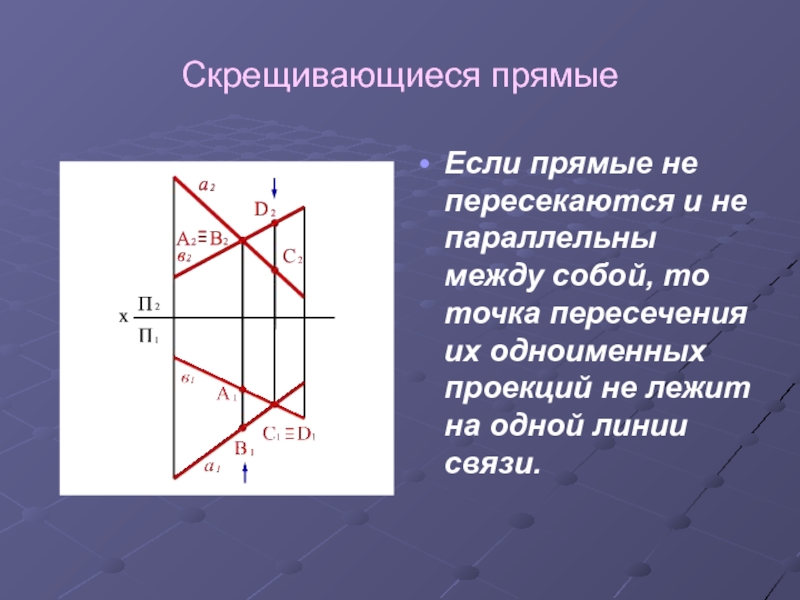
- 13. Скрещивающиеся прямыеЕсли прямые не пересекаются и не
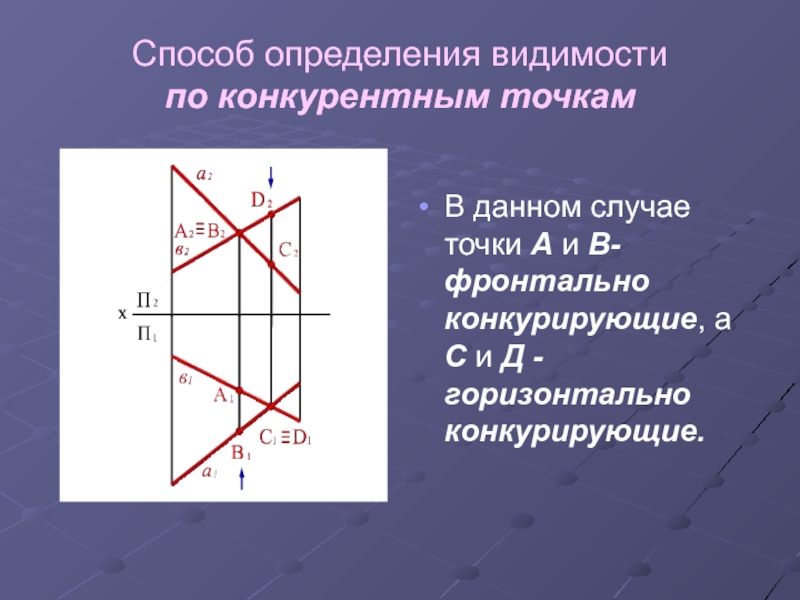
- 14. Способ определения видимости по конкурентным точкамВ
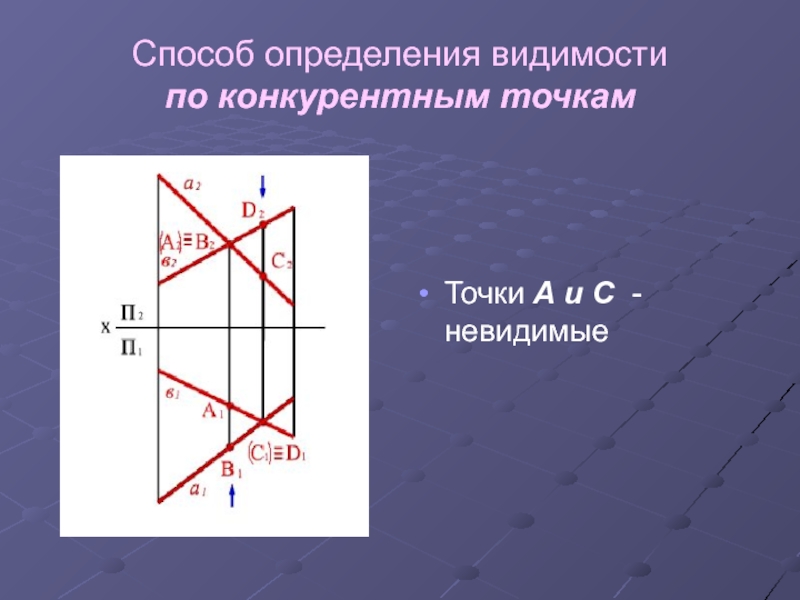
- 15. Способ определения видимости по конкурентным точкамТочки А и С - невидимые
- 16. Скачать презентанцию
Взаимное расположение двух прямыхКак могут располагаться две прямые в пространстве?Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися.
Слайды и текст этой презентации
Слайд 2Взаимное расположение двух прямых
Как могут располагаться две прямые в пространстве?
Прямые
линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися.
Слайд 3Параллельные прямые
Параллельными называются две прямые, которые лежат в одной
плоскости и не имеют общих точек.
Слайд 4Параллельные прямые
Проекции параллельных прямых - параллельны.
Если ABCD то
A1B1C1D1; A2B2C2D2; A3B3C3D3
Слайд 5Профильные прямые
Особый случай представляют собой прямые, параллельные одной из
плоскостей проекций.
Слайд 6Профильные прямые
Если фронтальные и горизонтальные проекции профильных прямых параллельны, то
для оценки их взаимного положения необходимо сделать проекцию на профильную
плоскость.
Слайд 7Профильные прямые
В рассмотренном случае проекции отрезков на плоскости П3 пересекаются,
следовательно, прямые не параллельны.
Слайд 8Пересекающиеся прямые
Пересекающимися называются две прямые лежащие в одной плоскости
и имеющие одну общую точку.
Слайд 9Пересекающиеся прямые
Если прямые пересекаются, то точки пересечения их одноименных проекций
находится на одной линии связи
Слайд 10Пересекающиеся прямые?
Если одна из прямых параллельна какой-либо из плоскостей проекций,
по двум проекциям невозможно судить об их взаимном расположении.
Слайд 13Скрещивающиеся прямые
Если прямые не пересекаются и не параллельны между собой,
то точка пересечения их одноименных проекций не лежит на одной
линии связи.
Слайд 14Способ определения видимости
по конкурентным точкам
В данном случае точки А
и В- фронтально конкурирующие, а С и Д -горизонтально конкурирующие.
