Векторные модели данных (ВМ)

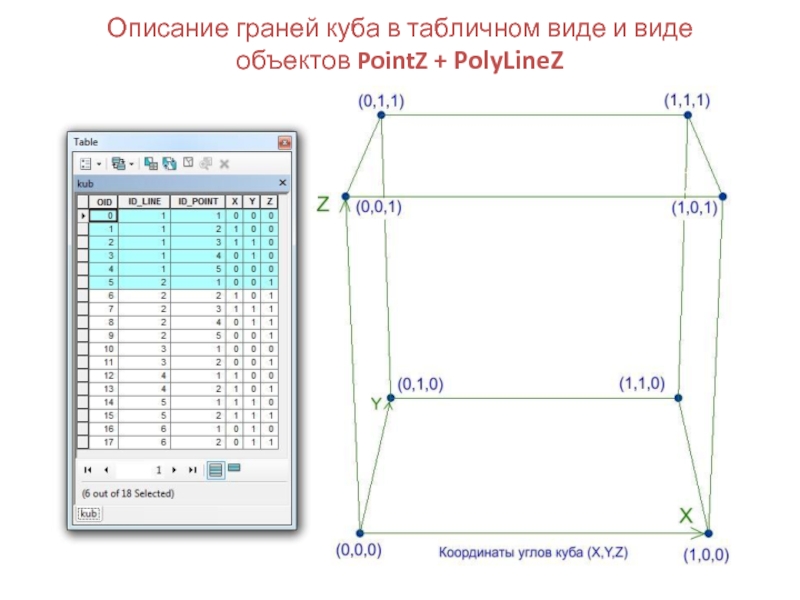
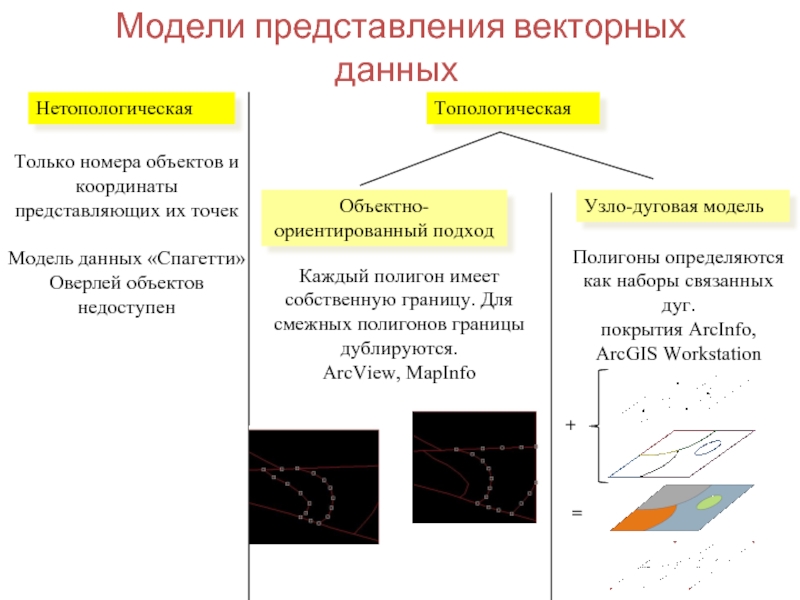
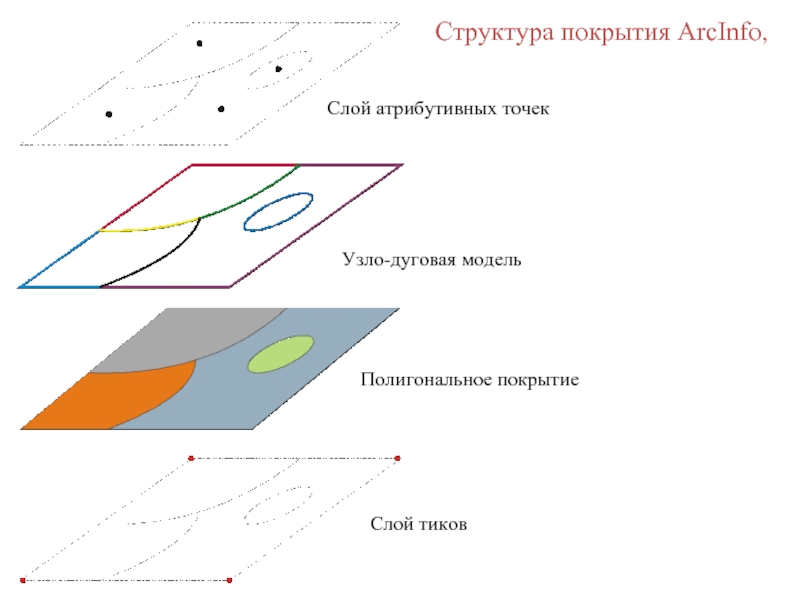
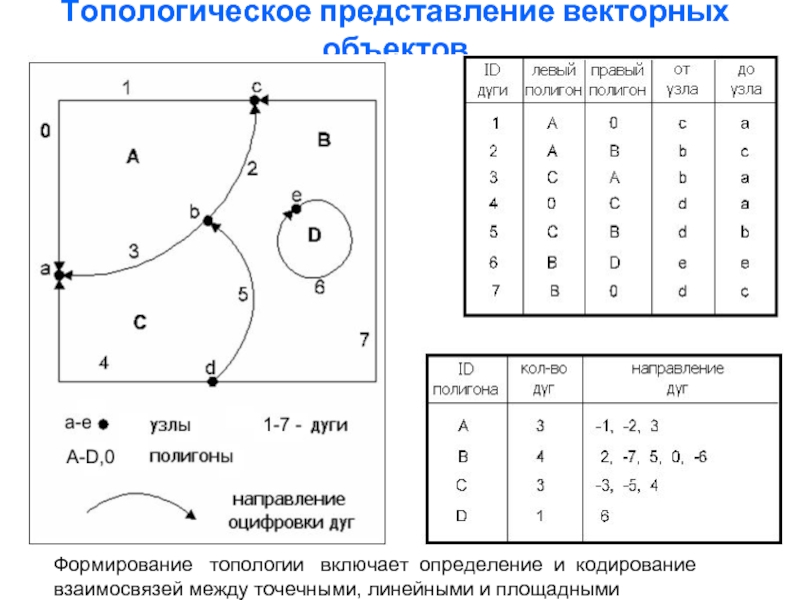
представление.
Векторные модели строятся на основе точек линий и полигонов. Физически

записываются как последовательности наборов координат.

Типы векторных данных:

Точка – 0-мерный геометрический объект, не имеющий длины и площади;
Линия – одномерный геометрический объект, не имеющий площади. Базовый элемент ВМ, через который определяются все остальные. Точка – «выродившаяся» линия нулевой длины. Полигон – одна замкнутая или последовательность, связанных между собой линий, с определенным внутренним содержанием;
Полигон – двумерная поверхность, заданная одной внешней границей. Может содержать одну или несколько внутренних границ, которые определяют т.н. острова или окна.
Графические примитивы – фигуры, форма которых определяется формулой (круги, эллипсы, сектора, квадраты, прямоугольники, правильные многоугольники, звезды, спирали, элементы выносок текста и т.д.)

y=6,8 2 x=3,2; y=2,1 3

x=7,3; y=4,5 4 x=8,1; y=1,5

Точки
(points)

Линии
(lines, arcs)

1

2

№ Координаты
1 x 1,2 2,7 6,5 7,8 y 5,2 7,3 5,8 6,1
2 x 1,1 2,4 3,1 6,6 7,9 y 0,8 4,2 1,9 1,3 3,8

Полигоны
(poligons)

1

2

№ Координаты
1 x = 1 2 4 6 5 1 y = 4 7 8 7 5 4
2 x = 3 6 7 8 7 5 5 3 3 y = 3 4 5 4 1 1 2 2 3
(первая и последняя точки имеют одинаковые координаты)
- атрибутивная точка, описывающая содержание полигона

(label, simbol)

+ PolyLineZ

в фигуру F1 без разрыва сплошности (деформации растяжения, сжатия, сдвига,

изгиба, кручения). К топологическим относятся проекционные преобразования.

Соседство
Связанность
Близость

Топологические свойства фигур более глубокие,
т.к., в отличие от метрических, сохраняются при деформациях.

Проекционные преобразования

связанных дуг.
покрытия ArcInfo, ArcGIS Workstation
Каждый полигон имеет собственную границу. Для

смежных полигонов границы дублируются.
ArcView, MapInfo

Только номера объектов и координаты
представляющих их точек

Модель данных «Спагетти»
Оверлей объектов недоступен

+

=

только в конечных узлах
Любая целая дуга принадлежит двум полигонам.

Висячая дуга – одному.
Граница любого полигона состоит из целых дуг, а не из их частей
Дуги имеют направление и соответственно правую и левую сторону

Топологическая концепция

кодирование
взаимосвязей между точечными, линейными и площадными объектами.

неориентированными. Если линия не имеет продольной оси симметрии, т.е. несет

какие-либо навесные символы (для изолиний это бергштрихи), то она относится к классу ориентированных ЛО. Их оцифровка должна осуществляться по правилу “правой руки”, т.е. навесной символ на линии при вводе должен располагаться с правой стороны.
Изолинии цифруются в соответствии со следующим правилом: область меньших значений изображаемого параметра должна лежать справа от дуги, задающей изолинию.
Примеры ориентированных линейных объектов
Я (несогласные границы, шарьяжи, границы оползней)
В каком направлении должны быть оцифрованы эти линии?
Если направление аппроксимирующей линии безразлично, то это неориентированный ЛО. Пример неориентированного ⎯ обычная согласная геологическая граница.
Кроме того, к классу ориентированных линейных объектов относятся все границы самостоятельных площадных объектов (границы месторождений полезных ископаемых, выражаемых в масштабе карты, границы ореолов рассеяния, границы типов и форм рельефа, водные акватории, лесные массивы и т.п.), а так же изолинии. Границы площадных объектов цифруются в направлении по часовой стрелке (так, чтобы площадь объекта лежала справа от границы).
Я В каком направлении должны быть оцифрованы границы полигонов?

(поверх имеющегося)
- занесение объекта

в другой слой

Ошибки оцифровки:

образование петель

разрыв линии

недоввод

перехлест

двойное цифрование

Метрическая корректность (относительная точность ввода согласно требуемых допусков)

Топологическая корректность
(точность соотношений)