Трехгранный угол

сумма любых двух из них больше третьего.
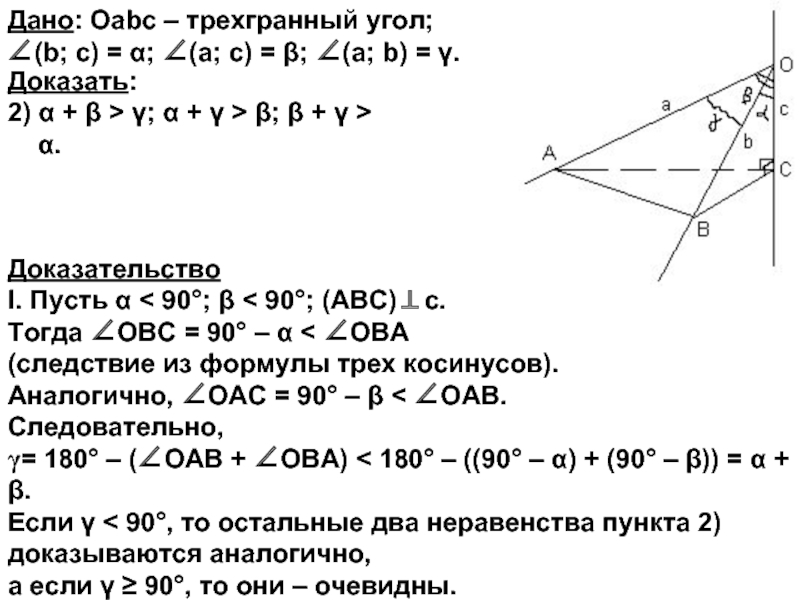
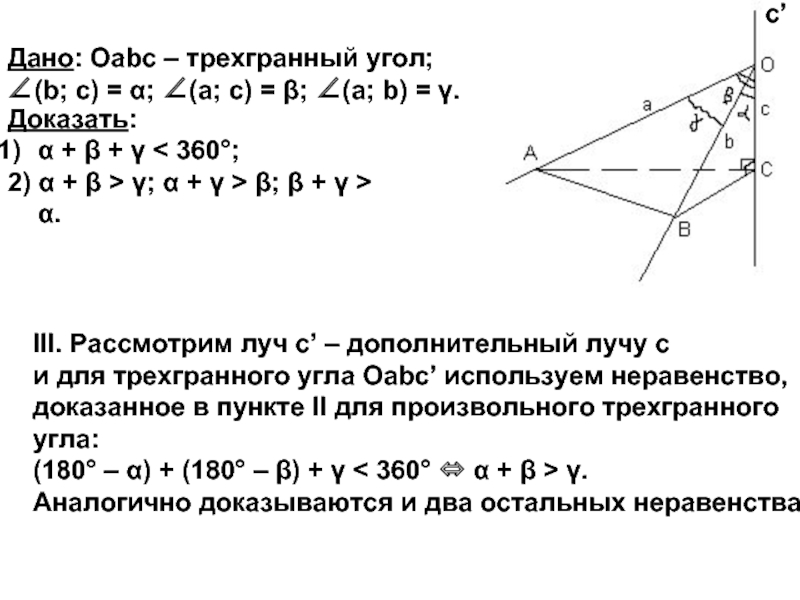
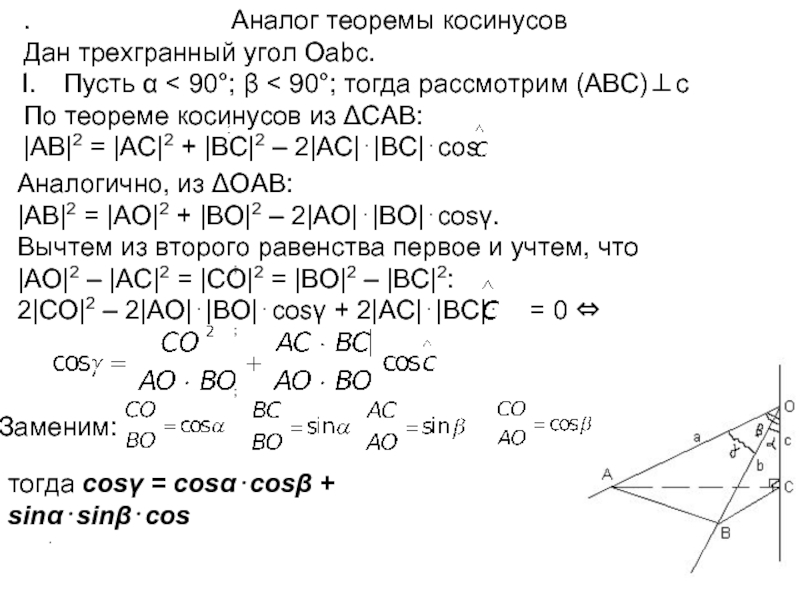
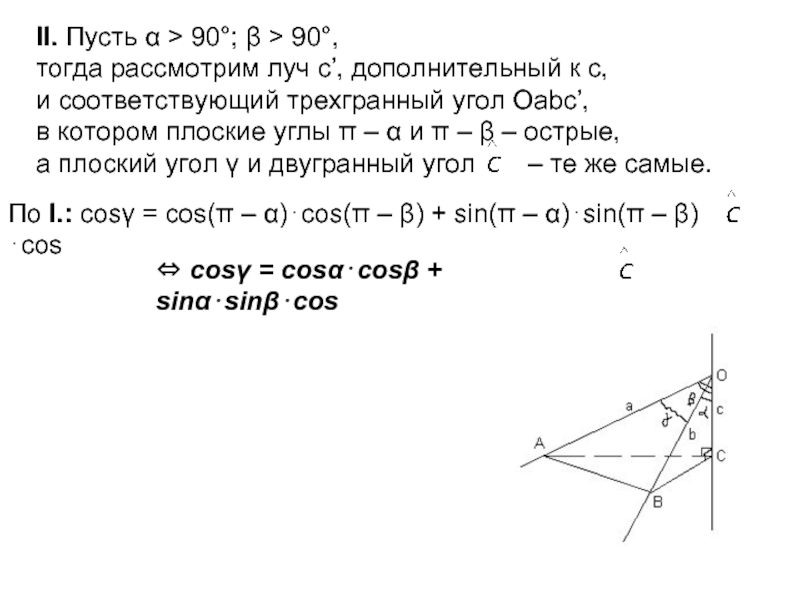
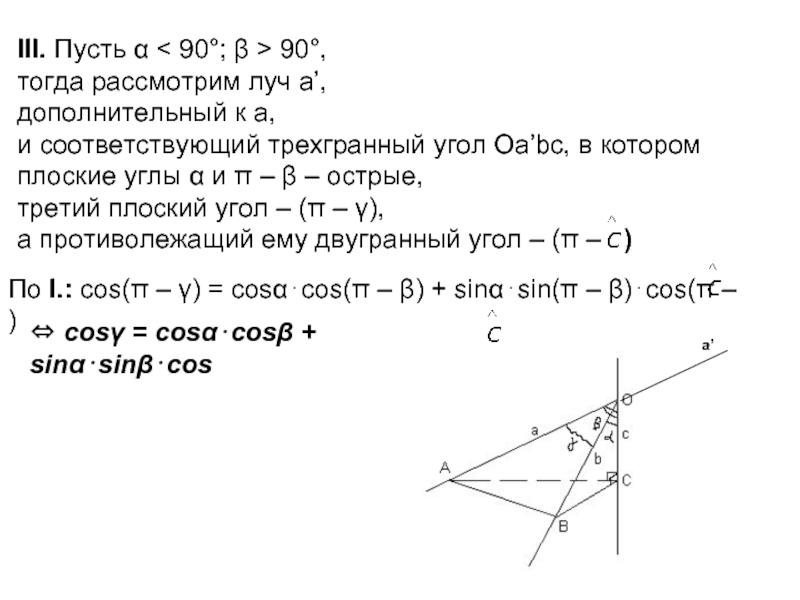
Дано: Оabc – трехгранный

угол;
∠(b; c) = α; ∠(a; c) = β; ∠(a; b) = γ.

Основное свойство трехгранного угла.

Доказать:
α + β + γ < 360°;
2) α + β > γ; α + γ > β; β + γ > α.

Тогда ∠ОВС = 90° – α < ∠ОВА
(следствие из

формулы трех косинусов).
Аналогично, ∠ОАС = 90° – β < ∠ОAВ.
Следовательно,
= 180° – (∠ОАB + ∠ОBA) < 180° – ((90° – α) + (90° – β)) = α + β.
Если γ < 90°, то остальные два неравенства пункта 2)
доказываются аналогично,
а если γ ≥ 90°, то они – очевидны.

Дано: Оabc – трехгранный угол;
∠(b; c) = α; ∠(a; c) = β; ∠(a; b) = γ.

Доказать:
2) α + β > γ; α + γ > β; β + γ > α.

прямой и
плоскостью применима формула:
2) Угол между прямой и

плоскостью –
наименьший из углов, которая эта прямая,
образует с прямыми этой плоскости.

C’
так, что |OA’| = |OB’| = |OC’|
Тогда треугольники A’OB’,

B’OC’ и С’OA’ –
равнобедренные, а их углы при основаниях 1 – 6 – острые.

Для трехгранных углов с вершинами A’, B’ и C’ применим
неравенства, доказанные в пункте I:
∠С’А’B’ < ∠1 + ∠6; ∠А’B’C’ < ∠2 + ∠3; ∠B’С’А’ < ∠4 + ∠5.
Сложим эти неравенства почленно,
тогда 180° < (∠1 + ∠2) + (∠3 + ∠4) + (∠5 + ∠6) =
= (180° – γ) + (180° – α) + (180° – β) ⇒ α + β + γ < 360°.

Дано: Оabc – трехгранный угол;
∠(b; c) = α; ∠(a; c) = β; ∠(a; b) = γ.

Доказать:
α + β + γ < 360°;
2) α + β > γ; α + γ > β; β + γ > α.

трехгранного угла Оabc’ используем неравенство,
доказанное в пункте II для произвольного

трехгранного
угла:
(180° – α) + (180° – β) + γ < 360° ⇔ α + β > γ.
Аналогично доказываются и два остальных неравенства.

Дано: Оabc – трехгранный угол;
∠(b; c) = α; ∠(a; c) = β; ∠(a; b) = γ.

Доказать:
α + β + γ < 360°;
2) α + β > γ; α + γ > β; β + γ > α.

с’

120°.

плоские и двугранные углы.
Признаки равенства трехгранных углов.
Трехгранные углы

равны, если у них соответственно равны:

два плоских угла и двугранный угол между ними;
2) два двугранных угла и плоский угол между ними;
3) три плоских угла;
4) три двугранных угла.

90°; тогда рассмотрим (ABC)⊥с
По теореме косинусов из ΔCАВ:
|AB|2

= |AC|2 + |BC|2 – 2|AC|⋅|BC|⋅cos

Аналог теоремы косинусов

Аналогично, из ΔOАВ:
|AB|2 = |AO|2 + |BO|2 – 2|AO|⋅|BO|⋅cosγ.
Вычтем из второго равенства первое и учтем, что
|AO|2 – |AC|2 = |CO|2 = |BO|2 – |BC|2:
2|CO|2 – 2|AO|⋅|BO|⋅cosγ + 2|AC|⋅|BC|⋅ = 0 ⇔

.

;

;

;

тогда cosγ = cosα⋅cosβ + sinα⋅sinβ⋅cos

Заменим:

луч с’, дополнительный к с,
и соответствующий трехгранный угол Оаbс’,

в котором плоские углы π – α и π – β – острые,
а плоский угол γ и двугранный угол – те же самые.

По I.: cosγ = cos(π – α)⋅cos(π – β) + sin(π – α)⋅sin(π – β)⋅cos

⇔ cosγ = cosα⋅cosβ + sinα⋅sinβ⋅cos

луч a’,
дополнительный к a,
и соответствующий трехгранный угол Оа’bс,

в котором
плоские углы α и π – β – острые,
третий плоский угол – (π – γ),
а противолежащий ему двугранный угол – (π – )

По I.: cos(π – γ) = cosα⋅cos(π – β) + sinα⋅sin(π – β)⋅cos(π – )

⇔ cosγ = cosα⋅cosβ + sinα⋅sinβ⋅cos

a’

тогда γ =
и равенство, очевидно, выполняется.
Если же только один

из этих углов,
например, β = 90°,
то доказанная формула имеет вид:

cosγ = sinα⋅cos

⇔ cosγ = cos(90° – α)⋅cos

Следствие. Если

= 90°, то cosγ = cosα⋅cosβ –
аналог теоремы Пифагора!