Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение ортогонального проекцирования 11 класс
Содержание
- 1. Применение ортогонального проекцирования 11 класс
- 2. Применение ортогонального проекцирования
- 3. Задача 1. Условие:Изобразите сечение единичного куба A…D1,
- 4. KLMРешение:Ответ:
- 5. Задача 2. Условие:Изобразите сечение единичного куба A…D1,
- 6. Искомым сечением будет шестиугольник. Площадь его ортогональной
- 7. Задача 3. Условие:В прямой призме ABCA1B1C1 BK-биссектриса
- 8. . AK=t; KC=2t.Ответ: 3.
- 9. Если ортогональная проекция на плоскость α переводит
- 10. Задача 4. Условие:Дан правильный тетраэдр МАВС с
- 11. Решение:3. Точка О и прямая АН –
- 12. Слайд 12
- 13. В правильной усеченной четырехугольной пирамиде A…D1 со
- 14. Слайд 14
- 15. В правильной четырехугольной пирамиде SАВСD, все ребра
- 16. Слайд 16
- 17. Задача 7. Условие:В основании прямой призмы ABCDA1B1C1D1
- 18. 1 способ решения:
- 19. Решение 2 (угол между прямой и плоскостью)F
- 20. По теореме косинусов для треугольника EBG1:EG1^2=EB^2+BG^2-2*EB*BG1*cos120°=441/4EG1=21/2Используя теорему
- 21. Задача 8Дана правильная четырехугольная пирамида MABCD, стороны основания которой равны 7. Угол между прямыми DM и AL, L-середина ребра MB, равен 60°.Найдите высоту пирамиды.
- 22. AB=BC=CD=AD=7DM и AL скрещивающиеся прямыеDM||OL в плоскости
- 23. Задача 9В правильной четырехугольной пирамиде PABCD с основанием ABCD точка M -
- 24. МК - средняя линия треугольника АРВМК || АВ=> АВ
- 25. АН = НВDMKC симметрична относительно HPTDT=TCПлоскость симметрии
- 26. По свойству перпендикулярных плоскостей перпендикуляр, опущенный из
- 27. X- искомое расстояние. Найдем через S: S=(1/2)*HT*PL*x
- 28. Задача 10В прямоугольном параллелепипеде A…D1, AB=BC=10√2, AA1=2√7. Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол . Найдите площадь сечения.
- 29. Сначала нам нужно построить это сечение. Очевидно, что
- 30. Определим положение перпендикуляра, который лежит в плоскости
- 31. Найдем проекцию сечения BLMD на плоскостьоснования. Для этого найдем
- 32. SL1CM1 равен SBCD (отношение площадей подобныхфигур
- 33. Скачать презентанцию
Применение ортогонального проекцирования
Слайды и текст этой презентации
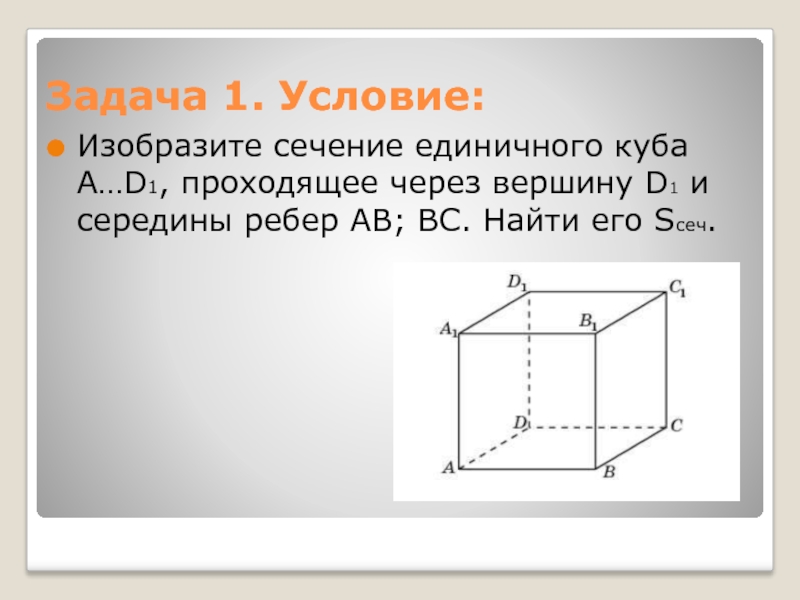
Слайд 3Задача 1. Условие:
Изобразите сечение единичного куба A…D1, проходящее через вершину
D1 и середины ребер AB; BC. Найти его Sсеч.
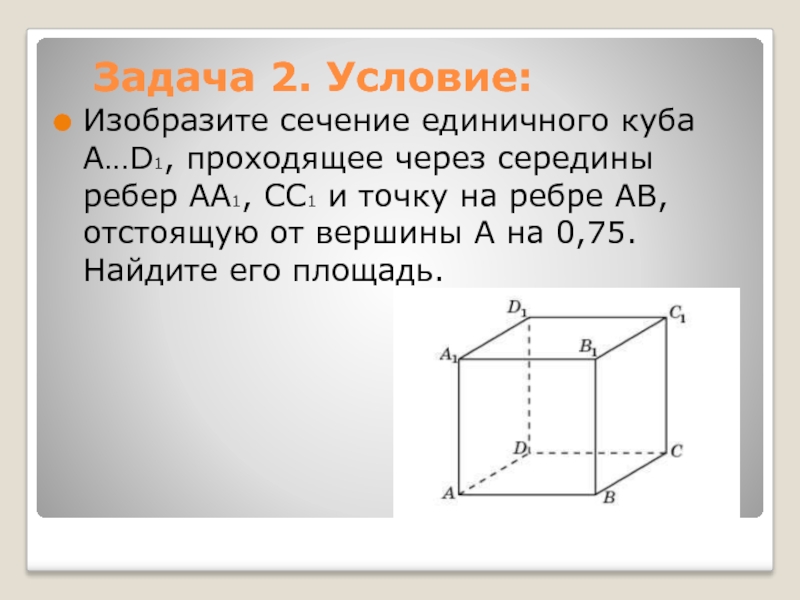
Слайд 5Задача 2. Условие:
Изобразите сечение единичного куба A…D1, проходящее через середины
ребер AA1, CC1 и точку на ребре AB, отстоящую от
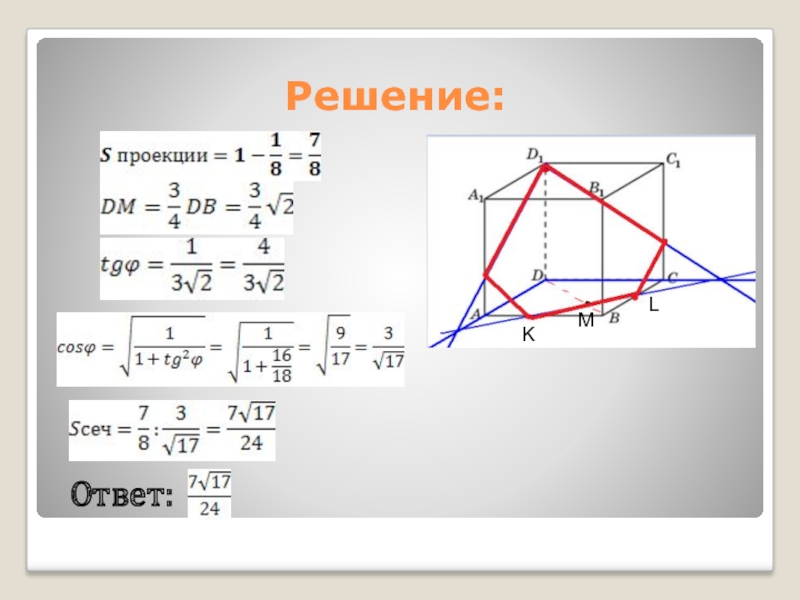
вершины A на 0,75. Найдите его площадь.Слайд 6Искомым сечением будет шестиугольник. Площадь его ортогональной проекции на плоскость
ABC равна ,косинус угла между плоскостью сечения и
плоскостью ABC равен . Площадь сечения равна .Ответ:
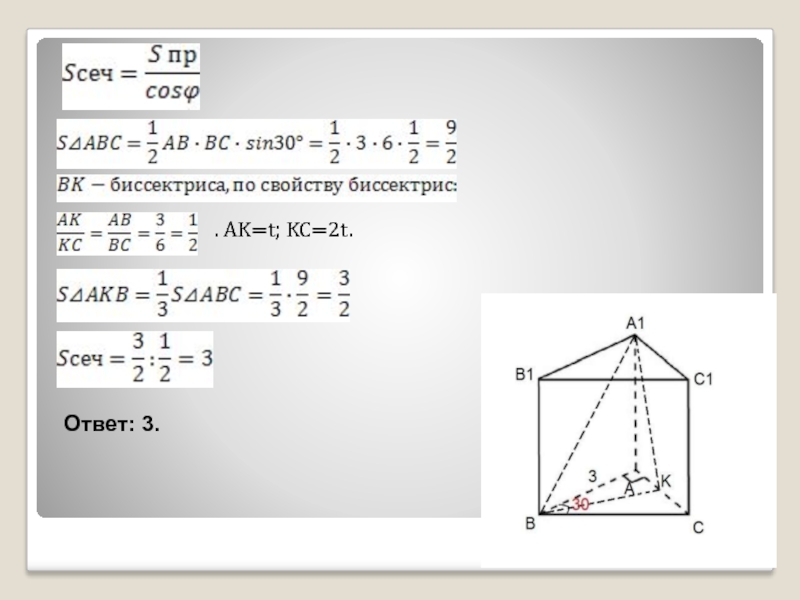
Слайд 7Задача 3. Условие:
В прямой призме ABCA1B1C1 BK-биссектриса основания ABC. Через
биссектрису и вершину А1 проведена плоскость, составляющая с плоскостью основания
60°. Найти Sсеч., если AB=3, BC=6, угол ABC=30°.Слайд 9Если ортогональная проекция на плоскость α переводит прямую a в
точку A, а прямую b в прямую b1, то расстояние
между скрещивающимися прямыми a и b равно расстоянию от А до прямой b1.Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой.
Слайд 10Задача 4. Условие:
Дан правильный тетраэдр МАВС с ребром 1. Найдите
расстояние между прямыми АL и МО, если L – середина
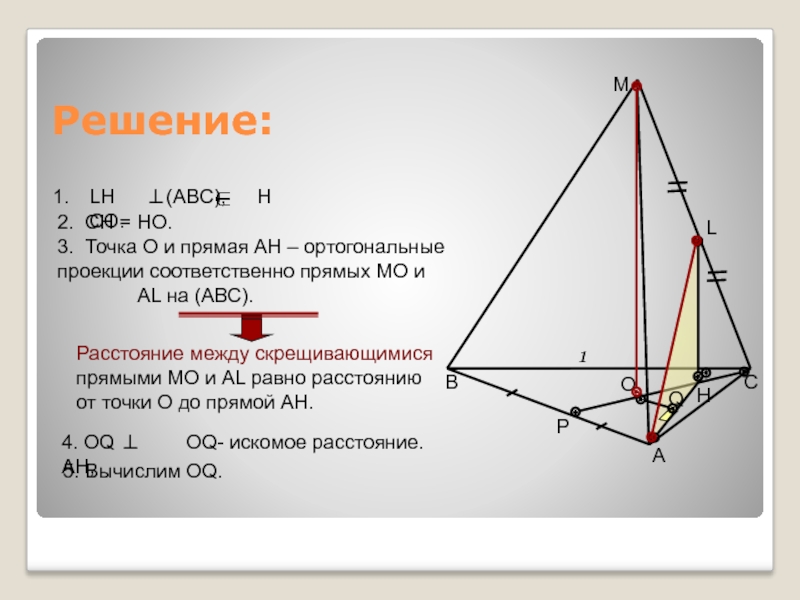
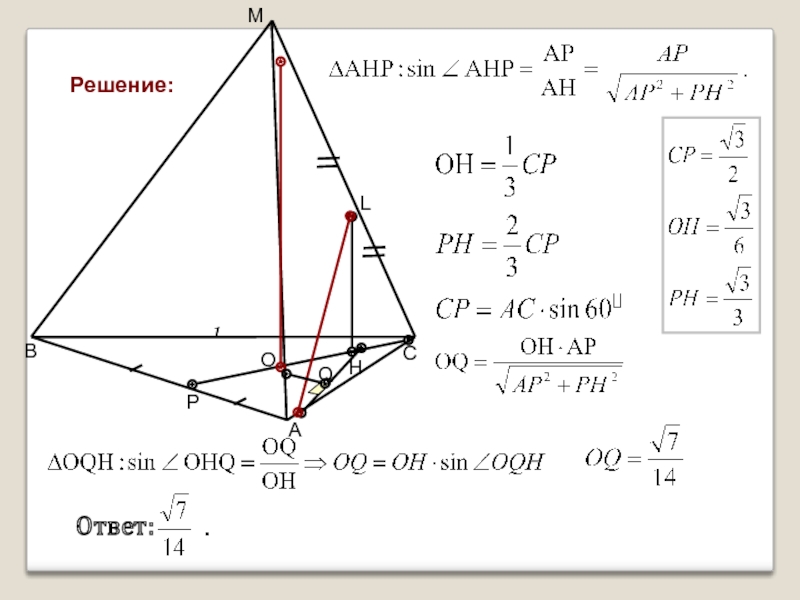
МС, О – центр грани АВС.Слайд 11Решение:
3. Точка О и прямая АН – ортогональные проекции соответственно
прямых МО и АL на (АВС).
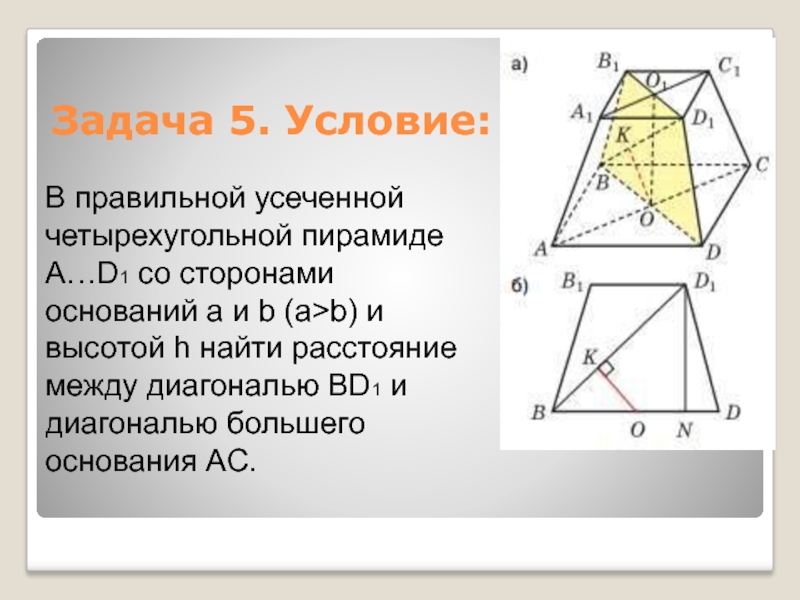
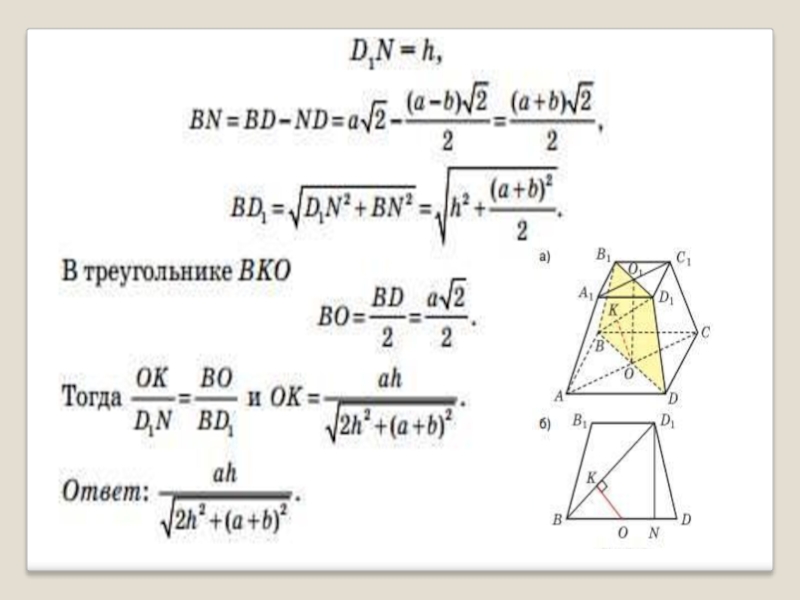
Слайд 13В правильной усеченной четырехугольной пирамиде A…D1 со сторонами оснований а
и b (a>b) и высотой h найти расстояние
между диагональю
BD1 и диагональю большего основания AC. Задача 5. Условие:
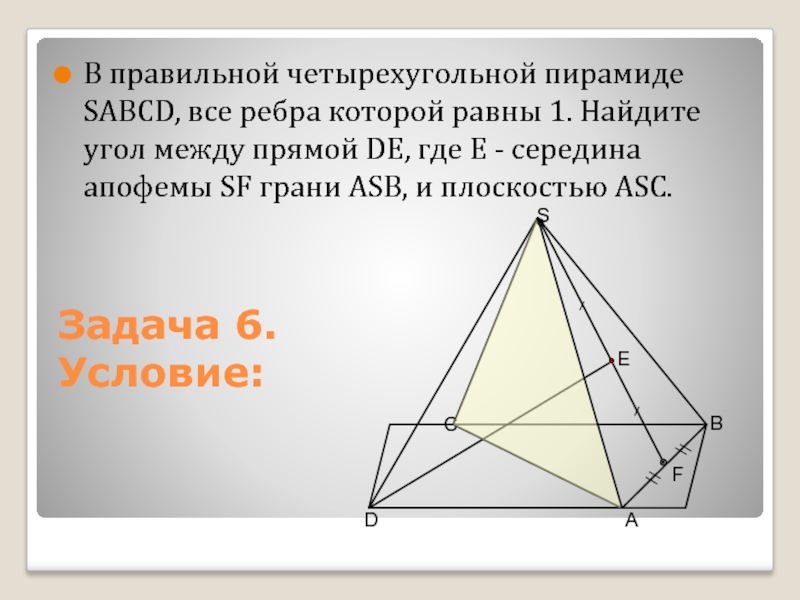
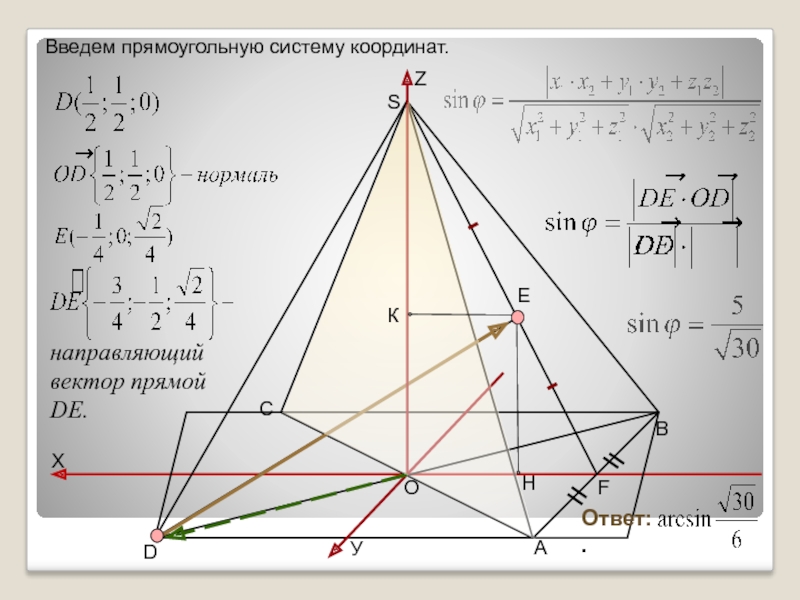
Слайд 15В правильной четырехугольной пирамиде SАВСD, все ребра которой равны 1.
Найдите угол между прямой DЕ, где Е - середина апофемы
SF грани АSВ, и плоскостью АSC.Задача 6.
Условие:
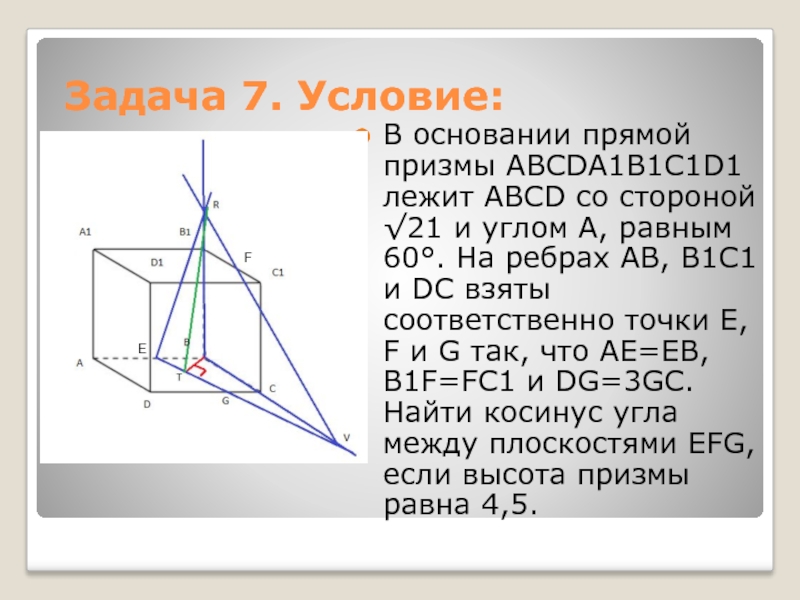
Слайд 17Задача 7. Условие:
В основании прямой призмы ABCDA1B1C1D1 лежит ABCD со
стороной √21 и углом A, равным 60°. На ребрах AB,
B1C1 и DC взяты соответственно точки E, F и G так, что AE=EB, B1F=FC1 и DG=3GC. Найти косинус угла между плоскостями EFG, если высота призмы равна 4,5.F
E
Слайд 19Решение 2 (угол между прямой и плоскостью)
F ⊥ (ABC)
F1-ортогональная проекция
точки F на плоскость и основание
BF1=F1C, FF1 ll BB1
G1-точка пересечения
прямых EG и BC. Треугольник EF1G1, лежащий в плоскости ABC,- ортогональная проекция треугольника EF1G1, лежащего в плоскости EFGИз подобия треугольников EBG1 и GCG1=> EB ll GC, CG1=BC, т.к. GC=¼DC=½EB
По теореме косинусов для треугольника
EBF1: EF1^2=EB^2+BF^2-2*EB*BF1*cos120°=63/4
EF=(3√7)/2
Из прямоугольных треугольников EFF1
и F1FG1: EF^2=EF1^2+F1F^2 =36
EF=6
FG1^2=F1G1^2+F1F^2=270/4
FG1=(3√30)/2
Слайд 20По теореме косинусов для треугольника EBG1:
EG1^2=EB^2+BG^2-2*EB*BG1*cos120°=441/4
EG1=21/2
Используя теорему косинусов для треугольника
EFG1:
cosLEFG1=(EF^2+FG1^2-EG1^2)/(2*EF*FG1)=-3/(8√30)
sinLEFG1=√(1-(- 3/(8√30)^2=√637/(8√10)
Находим площадь треугольника EFG1
SEFG1=½*EF*FG1*sinLEFG1=((9√3)/16)*√637
Находим площадь треугольника EF1G1:
SEF1G1=½*EF1*F1G1*sin150 °=(63√3)/16
Находим косинус
угла Y между плоскостями EFG1 и ABC по формуле:
cos Y= SEF1G1/SEFG1=1/√13
Ответ:1/√13
Слайд 21Задача 8
Дана правильная четырехугольная
пирамида MABCD, стороны основания которой равны 7. Угол между прямыми DM и AL, L-середина ребра MB, равен 60°.Найдите
высоту пирамиды.
Слайд 22AB=BC=CD=AD=7
DM и AL скрещивающиеся прямые
DM||OL в плоскости DMB
OL||MD, так как
OL-средняя линия треугольника BMD (по построению)
L ALO=60°
Докажем, что треугольник AOL-
прямоугольный(AC ⊥BD, AC ⊥OM, тогда => AC ⊥(BMD)
AC ⊥ любой прямой, лежащей в этой плоскости, т.е.
AC⊥OL, треугольник AOL-прямоугольный, LAOL=90°, LLAD=30°
tgLLAO=OL/OA=tg30 ° =√3/3
OL/((7*√2)/2)= √3/3
OL=((7√2)/2)* (√3/3)=(7√6)/6
DM=2OL
DM=2*((7√6)/6)=(7√6)/3
Треугольник OMD: OM=√(DM^2-OD^2)=
=(7√6)/6
Ответ: (7√6)/6
Слайд 23Задача 9
В правильной четырехугольной пирамиде PABCD с основанием ABCD
точка M - середина ребра РA, точка K - середина
ребра РB.
Найдите расстояние от вершины A до плоскости CMK,
если РC = 6, AB = 4.
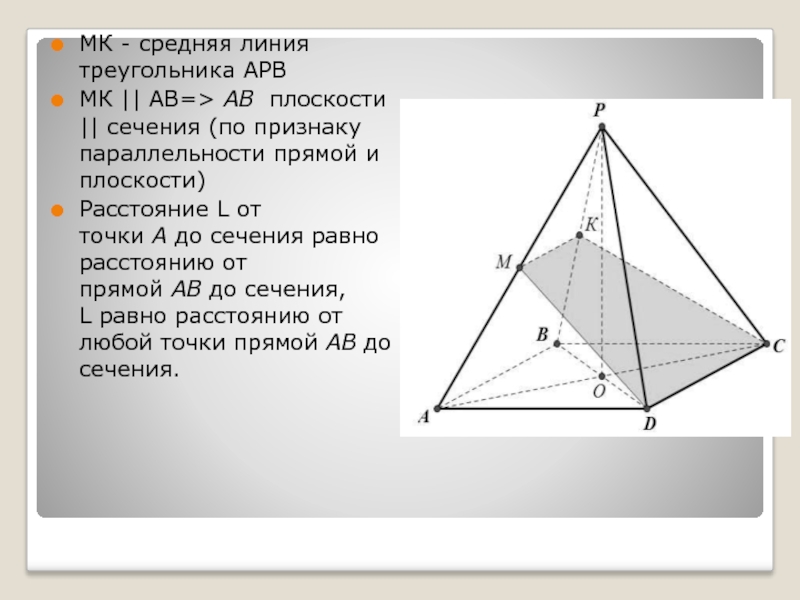
Слайд 24МК - средняя линия треугольника АРВ
МК || АВ=> АВ плоскости || сечения
(по признаку параллельности прямой и плоскости)
Расстояние L от точки А до сечения
равно расстоянию от прямой АВ до сечения,
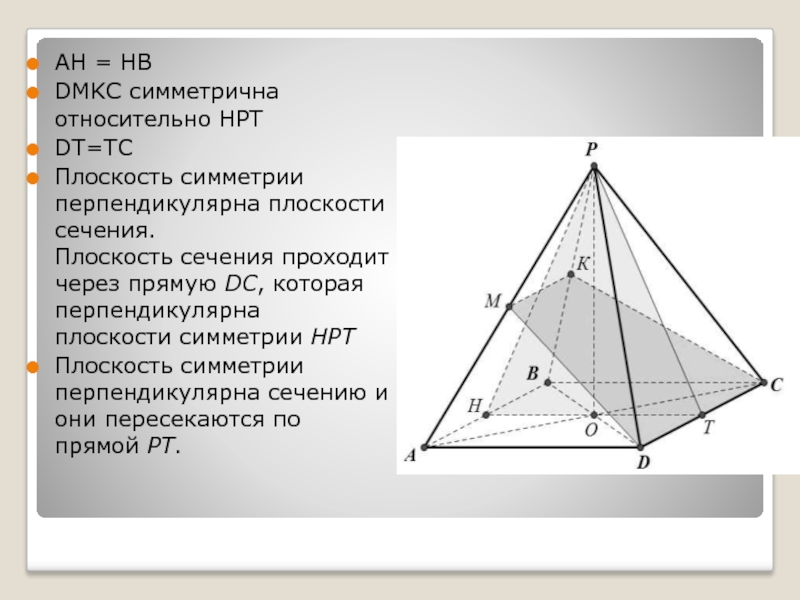
L равно расстоянию от любой точки прямой АВ до сечения.Слайд 25АН = НВ
DMKC симметрична относительно HPT
DT=TC
Плоскость симметрии перпендикулярна плоскости сечения.
Плоскость
сечения проходит через прямую DC, которая перпендикулярна
плоскости симметрии НРТ
Плоскость симметрии перпендикулярна сечению и
они пересекаются по прямой РТ.
Слайд 26По свойству перпендикулярных плоскостей перпендикуляр, опущенный из т. Н на
сечение, попадает точно на прямую РТ, то есть найти нам надо длину
именно этого перпендикуляра. Найдем высоту треугольника НРТ, проведённой к стороне РТ.X- искомое расстояние.
Найдем через S: S=½*HT*PL*x
Слайд 27X- искомое расстояние.
Найдем через S: S=(1/2)*HT*PL*x
1) PL = 0,5·РО,
т.к. PL - ср. линия
треугольника НРО. Найдём высоту пирамиды.
В прямоугольном треугольнике PОС: PС = 6 и
ОС
= 0,5·АС = 0,5·4√2 = 2√2.По теореме Пифагора находим
РО = √36 - 8 =√28 = 2√7. Значит, PL = √7.
2) НТ = ВС = АВ = 4. HL = 0,5·HO = 0,5·2 = 1,
LT = HT - HL = 4 - 1 = 3.
3) PT найдём по теореме Пифагора из
треугольника PLT: PT = √9 + 7 = 4.
Теперь можно искать высоту х,
проведённую к стороне РТ треугольника PTL: HT·PL = PT·x 4·√7 = 4·x x = √7 Ответ: √7
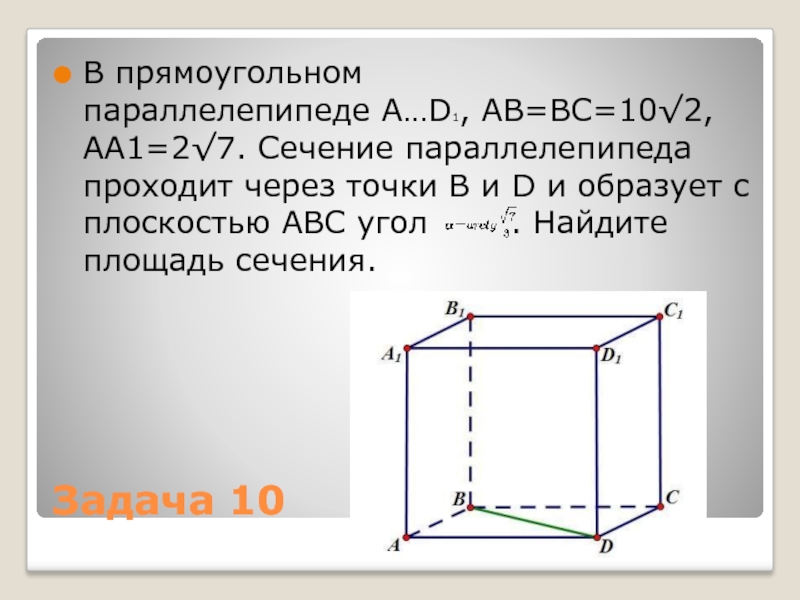
Слайд 28Задача 10
В прямоугольном параллелепипеде A…D1, AB=BC=10√2, AA1=2√7. Сечение параллелепипеда проходит через точки B и D и
образует с плоскостью ABC угол . Найдите площадь сечения.
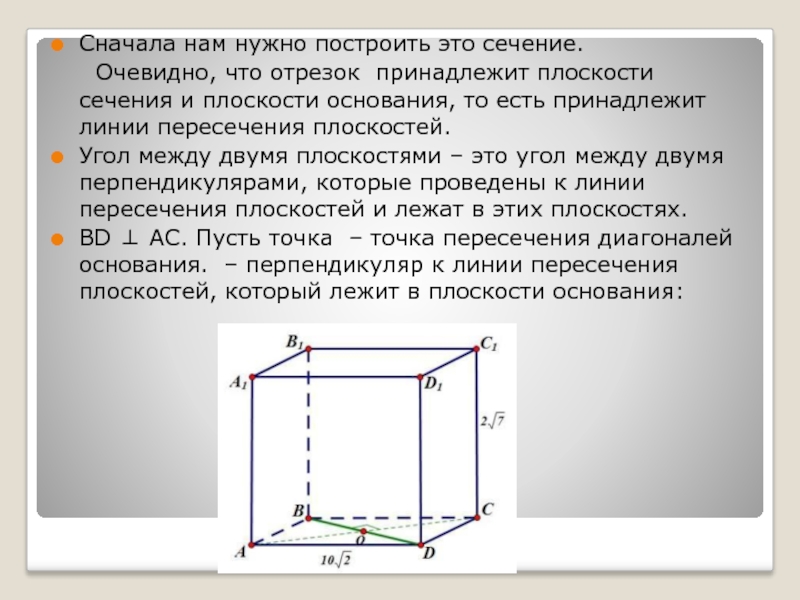
Слайд 29Сначала нам нужно построить это сечение.
Очевидно, что отрезок принадлежит плоскости сечения
и плоскости основания, то есть принадлежит линии пересечения плоскостей.
Угол между
двумя плоскостями – это угол между двумя перпендикулярами, которые проведены к линии пересечения плоскостей и лежат в этих плоскостях.BD ⊥ AC. Пусть точка – точка пересечения диагоналей основания. – перпендикуляр к линии пересечения плоскостей, который лежит в плоскости основания:
Слайд 30Определим положение перпендикуляра, который лежит в плоскости сечения. (Помним, что
если прямая перпендикулярна проекции наклонной, то она перпендикулярна и самой
наклонной. Ищем наклонную по ее проекции (OC) и углу между проекцией и наклонной). Найдем тангенс угла COC1 между OC1 и OC :=>
между плоскостью сечения и плоскостью
основания больше, чем между OC1 и OC.
То есть сечение расположено как-то так:
K- точка пересечение OP и A1C1. LM ll B1D1.
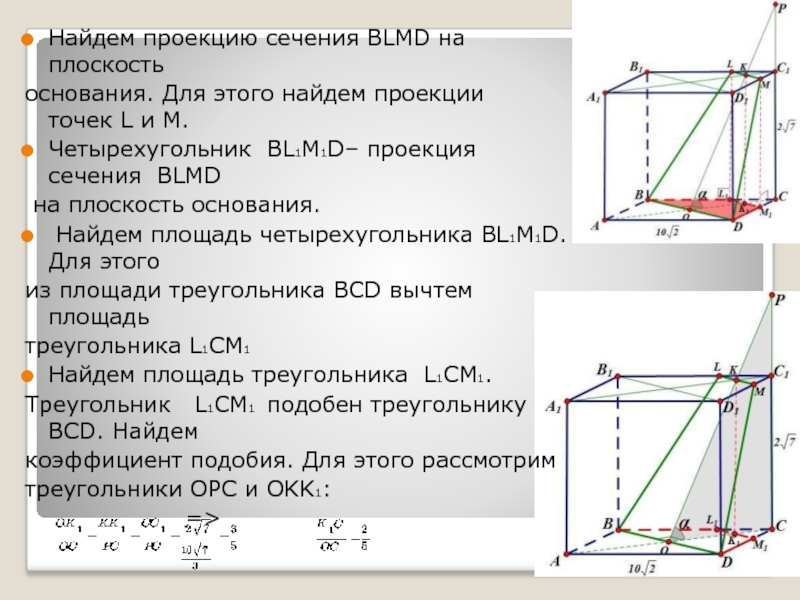
Слайд 31Найдем проекцию сечения BLMD на плоскость
основания. Для этого найдем проекции точек L и M.
Четырехугольник BL1M1D– проекция
сечения BLMD
на плоскость основания.
Найдем площадь четырехугольника BL1M1D. Для этого
из
площади треугольника BCD вычтем площадьтреугольника L1CM1
Найдем площадь треугольника L1CM1.
Треугольник L1CM1 подобен треугольнику BCD. Найдем
коэффициент подобия. Для этого рассмотрим
треугольники OPC и OKK1:
=>