Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок геометрии "Остроугольный, прямоугольный и тупоугольный треугольники"
Содержание
- 1. Урок геометрии "Остроугольный, прямоугольный и тупоугольный треугольники"
- 2. Сумма углов треугольника равна 180°.∠ А + ∠ В + ∠ С = 180°АВС
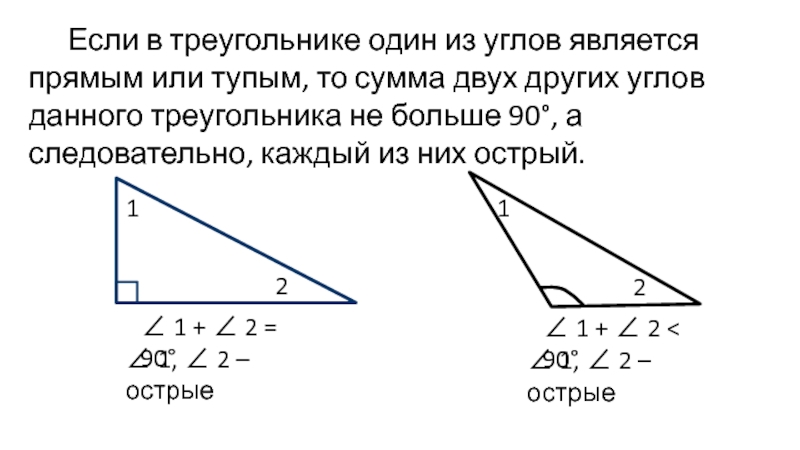
- 3. Если в треугольнике один из углов является
- 4. Остроугольный треугольник – это треугольник, у которого
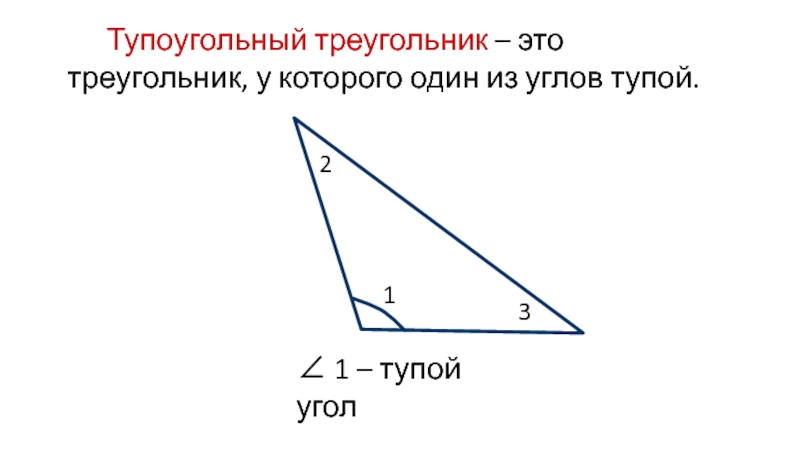
- 5. Тупоугольный треугольник – это треугольник, у которого один из углов тупой. ∠ 1 – тупой угол132
- 6. Прямоугольный треугольник – это треугольник, у которого
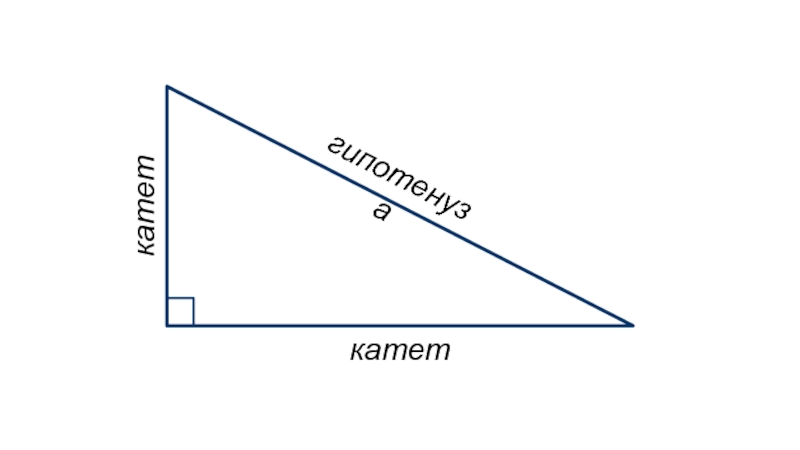
- 7. гипотенузакатеткатет
- 8. Слайд 8
- 9. Задача. Докажите, что угол с вершиной на
- 10. Задача. Докажите, что если в равнобедренном треугольнике
- 11. СВА2) Пусть ∠ В = 60°. 60°Тогда
- 12. Задача. Докажите, что в прямоугольном ∆ АВС
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Если в треугольнике один из углов является прямым или тупым,
то сумма двух других углов данного треугольника не больше 90°,
а следовательно, каждый из них острый.∠ 1 + ∠ 2 = 90°
∠ 1 + ∠ 2 < 90°
∠ 1, ∠ 2 – острые
∠ 1, ∠ 2 – острые
Слайд 4Остроугольный треугольник – это треугольник, у которого все три угла
острые.
∠ 1, ∠ 2, ∠ 3 – острые углы
1
3
2
Слайд 5Тупоугольный треугольник – это треугольник, у которого один из углов
тупой.
∠ 1 – тупой угол
1
3
2
Слайд 6Прямоугольный треугольник – это треугольник, у которого один из его
углов является прямым.
1
3
2
∠ 1 – прямой угол
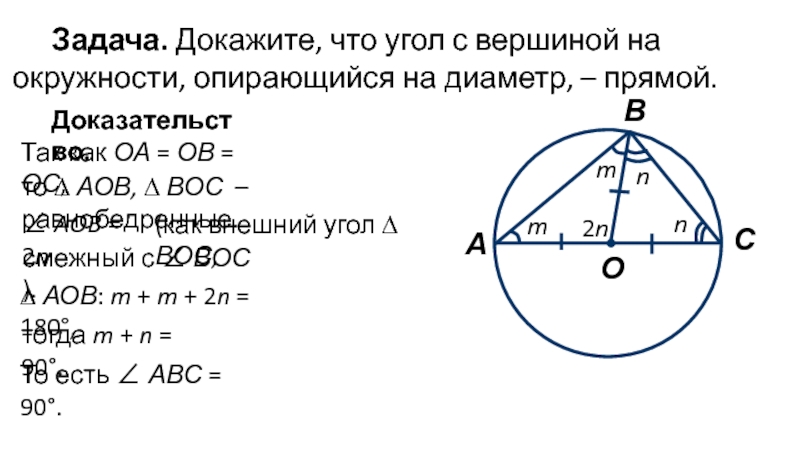
Слайд 9Задача. Докажите, что угол с вершиной на окружности, опирающийся на
диаметр, – прямой.
Доказательство.
О
С
В
А
Так как ОА = ОВ = ОС,
то
∆ АОВ, ∆ ВОС – равнобедренные.m
m
n
n
смежный с ∠ ВОС ).
(как внешний угол ∆ ВОС,
∆ АОВ: m + m + 2n = 180°,
тогда m + n = 90°.
То есть ∠ АВС = 90°.
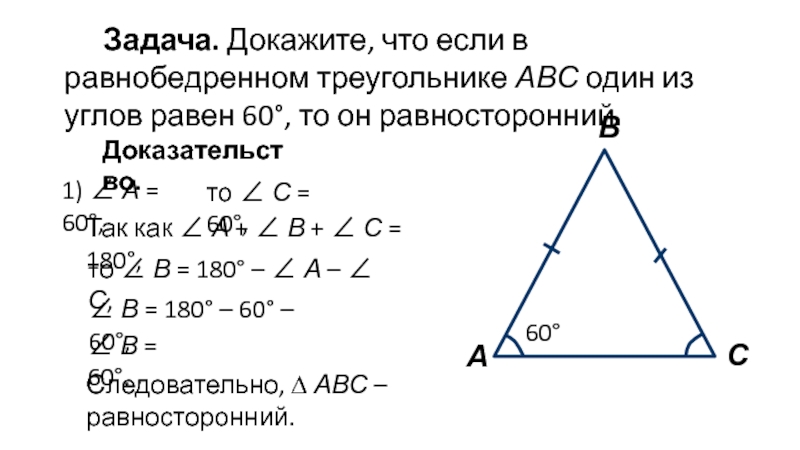
Слайд 10Задача. Докажите, что если в равнобедренном треугольнике АВС один из
углов равен 60°, то он равносторонний.
Доказательство.
С
В
А
1) ∠ А = 60°,
то ∠ С = 60°,
60°
Так как ∠ А + ∠ В + ∠ С = 180°,
то ∠ В = 180° – ∠ А – ∠ С,
∠ В = 180° – 60° – 60°,
∠ В = 60°.
Следовательно, ∆ АВС – равносторонний.
Слайд 11С
В
А
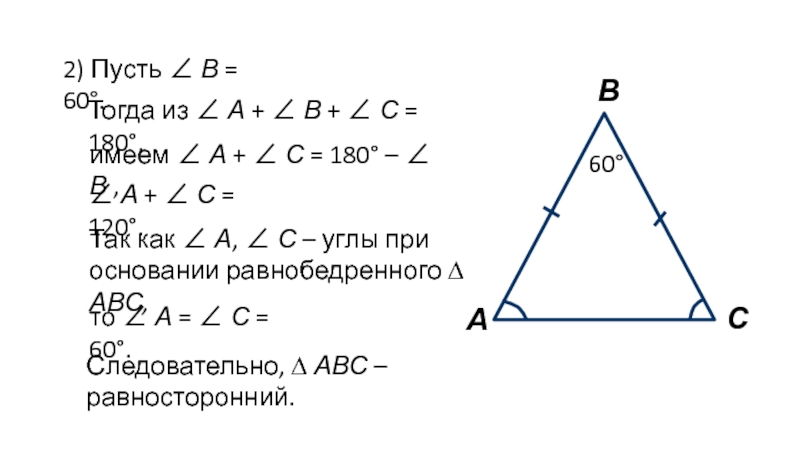
2) Пусть ∠ В = 60°.
60°
Тогда из ∠ А
+ ∠ В + ∠ С = 180°,
имеем ∠
А + ∠ С = 180° – ∠ В , ∠ А + ∠ С = 120°.
то ∠ А = ∠ С = 60°.
Следовательно, ∆ АВС – равносторонний.
Так как ∠ А, ∠ С – углы при основании равнобедренного ∆ АВС,
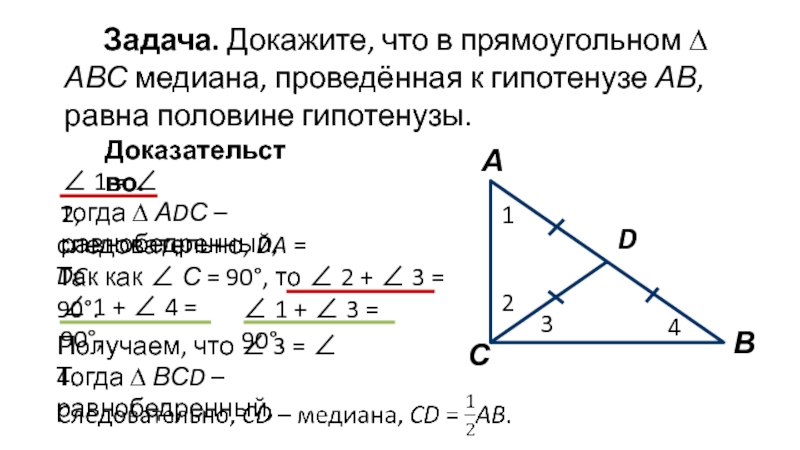
Слайд 12Задача. Докажите, что в прямоугольном ∆ АВС медиана, проведённая к
гипотенузе АВ, равна половине гипотенузы.
Доказательство.
С
В
А
3
4
тогда ∆ АDС – равнобедренный,
следовательно, DA
= DC.Так как ∠ С = 90°, то ∠ 2 + ∠ 3 = 90°.
∠ 1 + ∠ 4 = 90°,
∠ 1 + ∠ 3 = 90°.
Получаем, что ∠ 3 = ∠ 4.
Тогда ∆ ВСD – равнобедренный,