Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия и осевая симметрия
Содержание
- 1. Симметрия и осевая симметрия
- 2. Содержание: Определение симметрии, виды симметрии. Осевая симметрия. Теорема.
- 3. Симметрия – (от греч.) соразмерность, пропорциональность, одинаковость
- 4. Осевой симметрией с осью a называется такое
- 5. Докажем , что осевая симметрия есть движение.
- 6. ZYXOOMM11) Обозначим точку О – центр симметрии
- 7. ZYXOOMM12) Установим связь между координатами двух точек:M(x; y; z) и M1(x1; y1; z1). Z0 (M) = M1.
- 8. ZYXOOMM13)Если М Оz , то Оz ММ1 и
- 9. ZYXOOABA1B15) Рассмотрим А(x1; y1; z1), В(x2; y2;
- 10. ZYXOOABA1B1 тогда АВ=А1В1, т.е. Sоz - движение. 7)
- 11. По формуле расстояния между двумя точками находим
- 12. Скачать презентанцию
Содержание: Определение симметрии, виды симметрии. Осевая симметрия. Теорема.
Слайды и текст этой презентации
Слайд 3Симметрия – (от греч.) соразмерность, пропорциональность, одинаковость в расположении частей.
Виды
симметрии:
Слайд 4Осевой симметрией с осью a называется такое отображение пространства на
себя, при котором любая точка M переходит в симметричную ей
точку M1 относительно оси a.Симметрия простейших фигур
Слайд 6Z
Y
X
O
O
M
M1
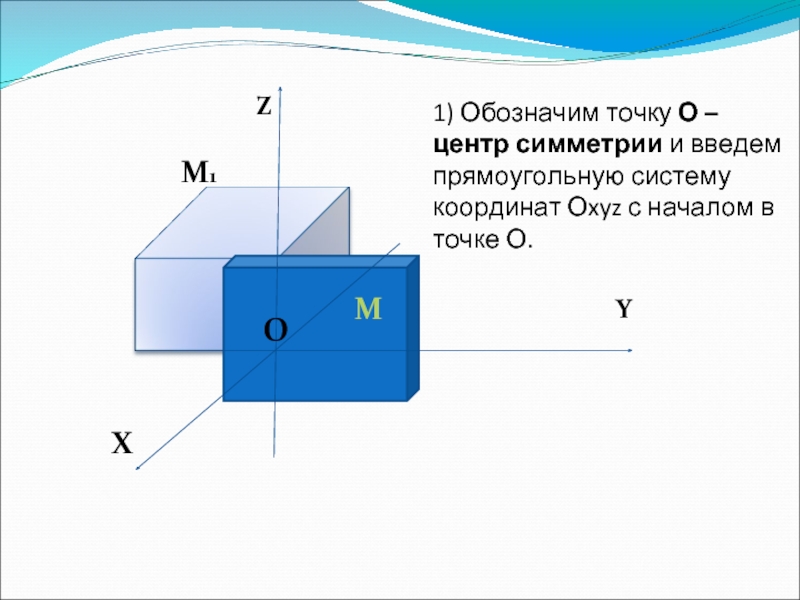
1) Обозначим точку О – центр симметрии и введем прямоугольную
систему координат Оxyz с началом в точке О.
Слайд 7Z
Y
X
O
O
M
M1
2) Установим связь между координатами двух точек:
M(x; y; z) и
M1(x1; y1; z1). Z0 (M) = M1.
Слайд 8Z
Y
X
O
O
M
M1
3)Если М Оz , то Оz ММ1 и проходит через середину.
4)
Т. к. Оz М1, то z =
z1.Оz проходит через середину ММ1 , то х = -х1, у = -у1.
Если точка М лежит на оси Оz, то х1 = х = 0, у1 = у = 0, z1= z = 0.
Слайд 9Z
Y
X
O
O
A
B
A1
B1
5) Рассмотрим А(x1; y1; z1),
В(x2; y2; z2)
6) А—> А1, В—>
В1,
тогда А1(-x1; -y1; z1),
В1(-x2; -y2; z2)
Слайд 10Z
Y
X
O
O
A
B
A1
B1
тогда АВ=А1В1, т.е. Sоz - движение.
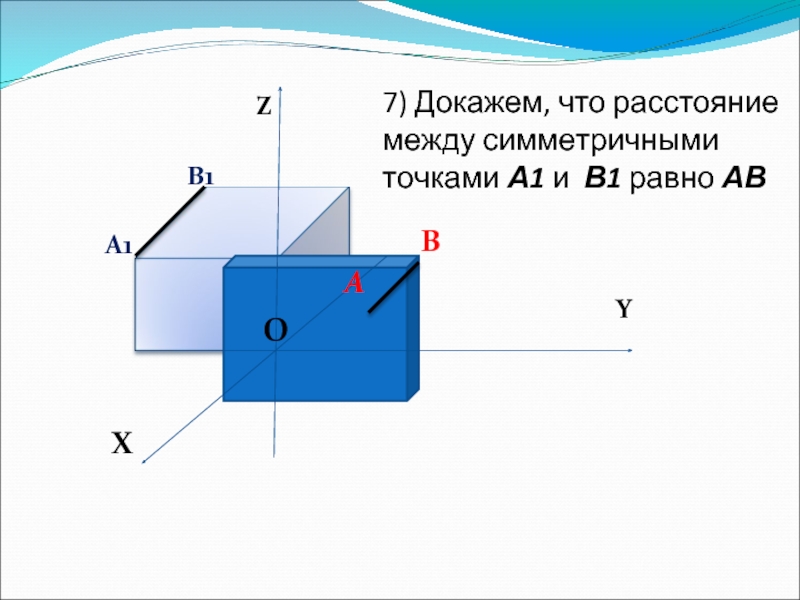
7) Докажем, что расстояние между
симметричными точками А1 и В1 равно АВ
Слайд 11По формуле расстояния между двумя точками находим :
тогда
АВ=А1В1, т.е. Sоz - движение.
тогда АВ=А1В1, т.е. Sоz - движение, что и
требовалось доказать.
Теги