Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пирамида. Решение задач 11 класс
Содержание
- 1. Пирамида. Решение задач 11 класс
- 2. 302Дано:ABCDS- пирамидаО – точка пересечения диагоналей параллелограммаАB
- 3. Слайд 3
- 4. Решение:По свойству параллелограмма найдем:BO = OD и
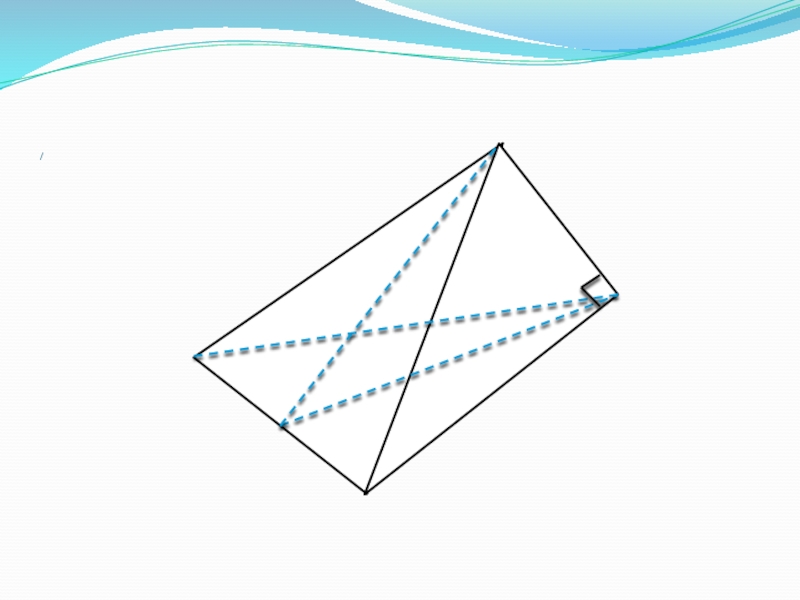
- 5. 310Дано:DABC – пирамида,DA ABC,AB =AC=25см,BC = 40см,DA = 8см.Найти Sбок
- 6. /
- 7. Решение:Sбок =SABD +SADC +SBDC;Sбок =SADC = DH*AC
- 8. 311Дано: DABC = пирамида, ADC – основание,AC=13см,AB=15 см,CB=14 см,AD ABC,AD=9 см. найти Sп.п.AK
- 9. .
- 10. Решение: DAB и DAC – прямоугольники;SBDA
- 11. .Построим АК ВС и отрезок DK.
- 12. .Итак, точка H принадлежит, а DK -
- 13. . KD = √AK2 + DA2 = √144+81
- 14. Скачать презентанцию
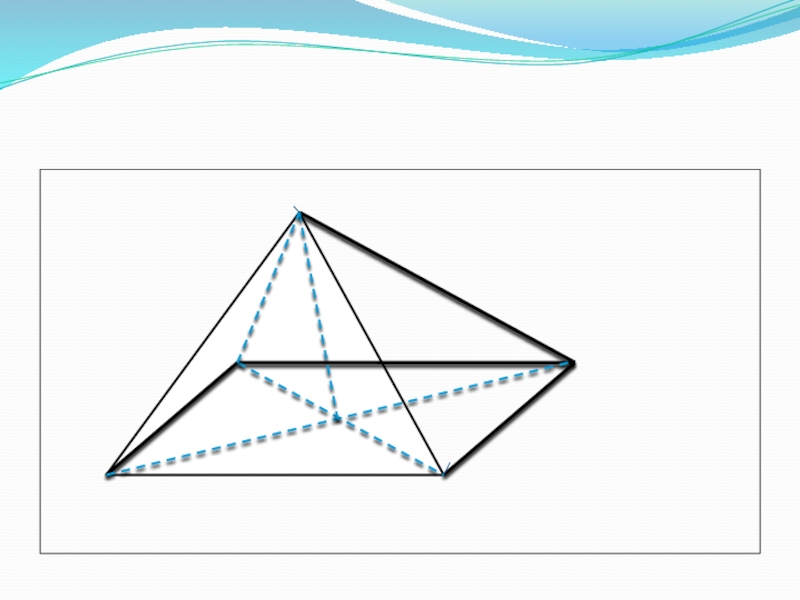
302Дано:ABCDS- пирамидаО – точка пересечения диагоналей параллелограммаАB = 3 смАD = 7 смAC = 6 смSO = 4 смНайдите боковые ребра пирамиды.
Слайды и текст этой презентации
Слайд 2302
Дано:
ABCDS- пирамида
О – точка пересечения диагоналей параллелограмма
АB = 3 см
АD
= 7 см
ребра пирамиды.Слайд 4Решение:
По свойству параллелограмма найдем:
BO = OD и AO = OC
BO
пл.ABC, SO = 4 см
OSB =
OSD ( по двум катетам), тогда SB = SD;AOS = COS ( по двум катетам), тогда SB = SC;
Пусть AO = OC = ½ AC = 3 см, BO = OD = x
Из ACD по теореме косинусов имеем:
AD2 = AC2 + CD2 -2 AC *CD *cosA
72 = 62 + 32 – 2 *6 * 3 * cosA , 49 = 36+9-36 * cosA, 36cosA = -4;
cosA= -4/36 = -1/9
Из COD по теореме косинусов имеем:
X2 = 9+9+2*9*1/9 = 18+2=20, x =2√5 (см)
Из прямоугольного SOB по теореме Пифагора имеем:
SD = √SO2 + OD2 = √42 +20 = √36 = 6 (cм)
Из прямоугольного SOC по теореме Пифагора имеем:
SC = √SO2 + OC2 = √42 + 32 = √25 = 5 (см) , SC =SA =5 (см)
Ответ: 5см 5 см 6 см 6см
Слайд 7Решение:
Sбок =SABD +SADC +SBDC;
Sбок =SADC = DH*AC /2 = 8*25/2=100(см2)
Из
ABD по т. Пифагора имеем:
BD=√AB2+DA2 = √252+82 = √689
(см).Из BDM по т. Пифагора имеем:
AB2+DA2 = √252+82 = √689 (см).
DM2 = BD2 –BM2 = 689 – 400 = 289,
DM = 17
SBDC = (DM*BM)* ½*2 = 17*20=340 (см2)
Sбок = 100+100+340 = 540(см2)
Ответ: 540 см2
Слайд 8311
Дано:
DABC = пирамида,
ADC – основание,
AC=13см,
AB=15 см,
CB=14 см,
AD
ABC,
AD=9 см.
найти Sп.п.
AK
Слайд 10Решение:
DAB и DAC – прямоугольники;
SBDA = ½ DA
* BA = ½ * 9 * 15 (см2), SCDA=
½ DA * CA = ½ * 9 * 13 (см2).По формуле Герона имеем:
SABC = √p(p-a) (p-b) (p-c) , где a = 14, b = 15, c = 13, а p = (AB + AC +CB) /2 = (13 + 14 + 15) /2= 21 (см);
Слайд 11.
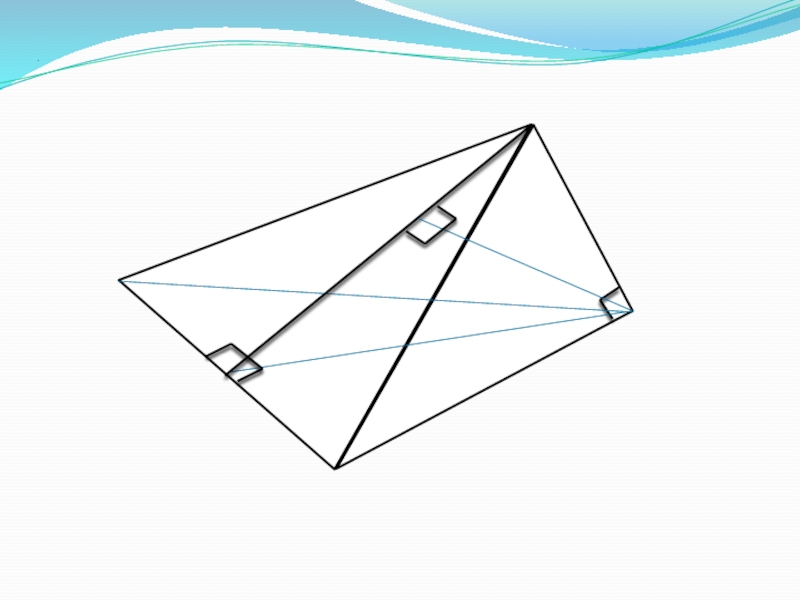
Построим АК ВС и отрезок DK. По теореме о
3-х перпендикулярах имеем DK BC. Проведем в плоскости ADK
отрезок AH DKAH DK – по построению, и AH BC, т.к AH принадлежит пл.ADK то пл.ADK BC.
AH перпендикулярна двум пересекающимся прямым плоскости BCD, а значит AH пл.BCD.
Слайд 12.
Итак, точка H принадлежит, а DK - высота грани DBC.
SDBC = ½ BS * DK.
Из ADK по т.
Пифагора имеем DK = √DA2 + AK2 = √ 81 + AK2SABC= ½ AK *BC = ½ AK * 14, следовательно, ½ AK * 14 = 84, AK = 12 (см), тогда DK = √81 + 144 = √225 = 15(см),
SDBC = ½ * 14 * 15 = 7 * 15 = 105 (см2).
Итак, Sп.п. = 9 * 15 /2 + 9 * 13 /2 + 84 + 105 = 9 * 28/ 2 + 189 = 315 (см2).
Слайд 13.
KD = √AK2 + DA2 = √144+81 = √225 =
15 (см), sinA = DA/KD = 9/15 = 3 /
5 Из KHA AH = KA*sinA = 12 * 3/5 = 36/5 = 7,2 (см)Ответ: а) 315 см2 ; б) 7.2 (см);