Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра высказываний. Основные операции алгебры высказываний
Содержание
- 1. Алгебра высказываний. Основные операции алгебры высказываний
- 2. Что такое логика?
- 3. LOGOS (ГРЕЧ.) – СЛОВО, ПОНЯТИЕ, РАССУЖДЕНИЕ, РАЗУМСЛОВО
- 4. ПОНЯТИЕ - ФОРМА МЫШЛЕНИЯ, В КОТОРОЙ ОТРАЖАЮТСЯ
- 5. МАТЕМАТИЧЕСКАЯ ЛОГИКА - ИЗУЧАЕТ ЛОГИЧЕСКИЕ СВЯЗИ И
- 6. ЭТАПЫ РАЗВИТИЯ ЛОГИКИ
- 7. АРИСТОТЕЛЬ (384-322 гг. до н.э.) -
- 8. СИЛЛОГИЗМ - РАССУЖДЕНИЕ, В КОТОРОМ ИЗ ЗАДАННЫХ
- 9. Декарт Рене (1596-1650, фр. философ, математик) РЕКОМЕНДОВАЛ В ЛОГИКЕ ИСПОЛЬЗОВАТЬ МАТЕМАТИЧЕСКИЕ МЕТОДЫ.
- 10. Лейбниц Г.В. (1646-1716, нем. ученый и
- 11. Джордж Буль (1815-1864, анл.) - основоположник
- 12. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
- 13. Логика оказала влияние на развитие математики, прежде
- 14. 1938 г. – американский математик и инженер
- 15. 5) Идеи и аппарат логики используется в
- 16. ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ
- 17. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ
- 18. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)
- 19. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) -Определение: КОНЪЮНКЦИЯ ДВУХ
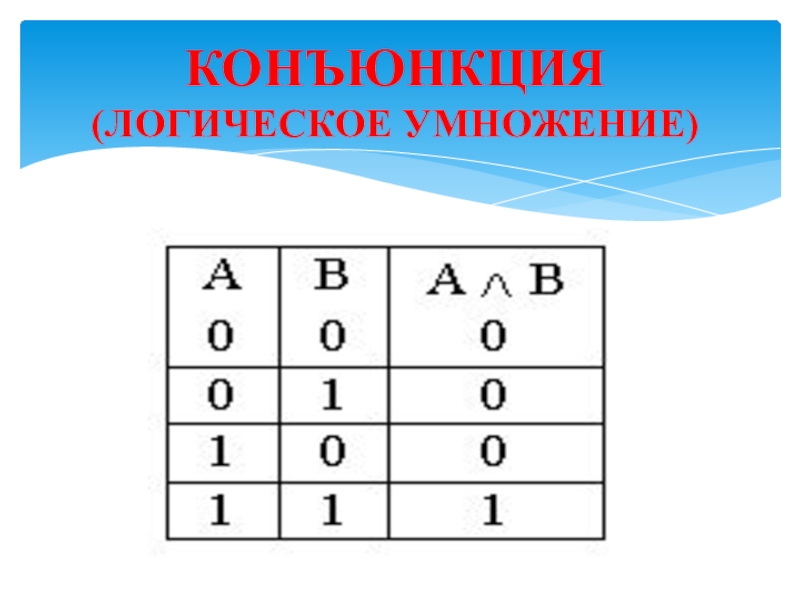
- 20. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ)
- 21. ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ЕСЛИ . .
- 22. ИМПЛИКАЦИЯ
- 23. ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ТОГДА И ТОЛЬКО
- 24. ЭКВИВАЛЕНЦИЯ
- 25. ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ:ИНВЕРСИЯ;КОНЪЮНКЦИЯ;ДИЗЪЮНКЦИЯ;ИМПЛИКАЦИЯ И ЭКВИВАЛЕНТНОСТЬ.
- 26. Слайд 26
- 27. Слайд 27
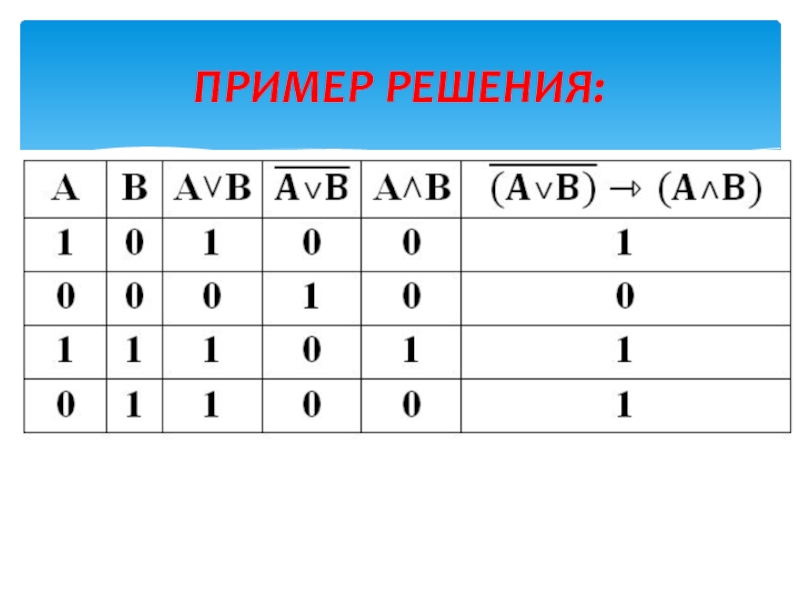
- 28. ПРИМЕР РЕШЕНИЯ:
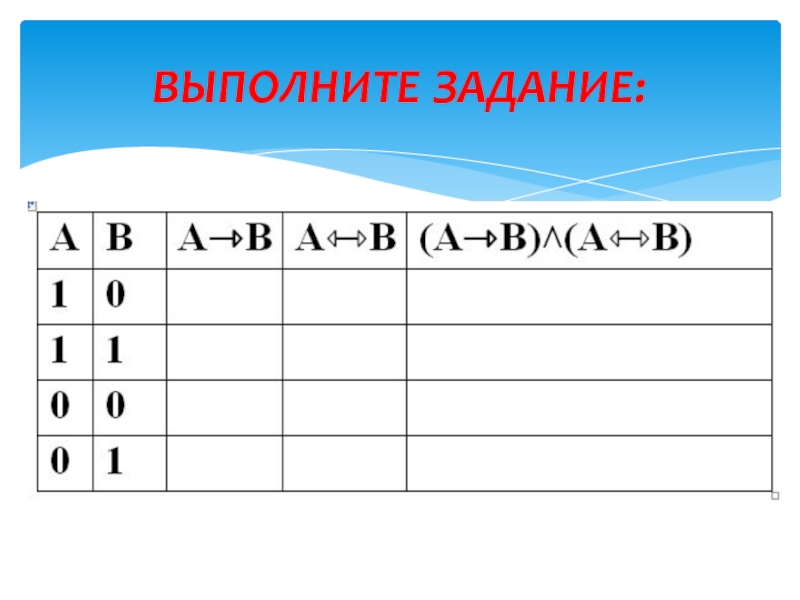
- 29. ТАБЛИЦА №1:ВЫПОЛНИТЕ ЗАДАНИЕ:
- 30. ТАБЛИЦА № 2ВЫПОЛНИТЕ ЗАДАНИЕ:
- 31. ТАБЛИЦА № 3ВЫПОЛНИТЕ ЗАДАНИЕ:
- 32. СОСТАВЬТЕ ВЫРАЖЕНИЕ В 7 ДЕЙСТВИЙ С ИСПОЛЬЗОВАНИЕМ
- 33. Скачать презентанцию
Что такое логика?
Слайды и текст этой презентации
Слайд 3LOGOS (ГРЕЧ.)
– СЛОВО, ПОНЯТИЕ, РАССУЖДЕНИЕ, РАЗУМ
СЛОВО «ЛОГИКА» ОБОЗНАЧАЕТ СОВОКУПНОСТЬ ПРАВИЛ,
КОТОРЫМ ПОДЧИНЯЕТСЯ ПРОЦЕСС МЫШЛЕНИЯ.
УМОЗАКЛЮЧЕНИЯ.
Слайд 4
ПОНЯТИЕ - ФОРМА МЫШЛЕНИЯ, В КОТОРОЙ
ОТРАЖАЮТСЯ СУЩЕСТВЕННЫЕ ПРИЗНАКИ
ОТДЕЛЬНОГО
ПРЕДМЕТА ИЛИ КЛАССА
ОДНОРОДНЫХ ПРЕДМЕТОВ. (ТРАПЕЦИЯ, ДОМ)
СУЖДЕНИЕ - МЫСЛЬ, В
КОТОРОЙ ЧТО-ЛИБО УТВЕРЖДАЕТСЯ ИЛИ ОТРИЦАЕТСЯ О ПРЕДМЕТАХ. (ВЕСНА НАСТУПИЛА, И ГРАЧИ ПРИЛЕТЕЛИ)УМОЗАКЛЮЧЕНИЕ - ПРИЕМ МЫШЛЕНИЯ, ПОСРЕДСТВОМ КОТОРОГО ИЗ ИСХОДНОГО ЗНАНИЯ ПОЛУЧАЕТСЯ НОВОЕ ЗНАНИЕ.
(ВСЕ МЕТАЛЛЫ - ПРОСТЫЕ ВЕЩЕСТВА)
Слайд 5
МАТЕМАТИЧЕСКАЯ ЛОГИКА - ИЗУЧАЕТ ЛОГИЧЕСКИЕ СВЯЗИ И ОТНОШЕНИЯ, ЛЕЖАЩИЕ В
ОСНОВЕ ЛОГИЧЕСКОГО (ДЕДУКТИВНОГО) ВЫВОДА.
ЛОГИКА (ФОРМАЛЬНАЯ) - НАУКА О ЗАКОНАХ И
ФОРМАХ ПРАВИЛЬНОГО МЫШЛЕНИЯ.
Слайд 7АРИСТОТЕЛЬ
(384-322 гг. до н.э.) - ОСНОВОПОЛОЖНИК ЛОГИКИ
КНИГИ:
«КАТЕГОРИИ»
«ПЕРВАЯ
АНАЛИТИКА»
«ВТОРАЯ АНАЛИТИКА»
(ИССЛЕДОВАЛ РАЗЛИЧНЫЕ ФОРМЫ РАССУЖДЕНИЙ , ВВЕЛ ПОНЯТИЕ СИЛЛОГИЗМА)
Слайд 8СИЛЛОГИЗМ - РАССУЖДЕНИЕ, В
КОТОРОМ ИЗ ЗАДАННЫХ ДВУХ
СУЖДЕНИЙ ВЫВОДИТСЯ
ТРЕТЬЕ.
АРИСТОТЕЛЬ ВЫДЕЛИЛ ВСЕ ПРАВИЛЬНЫЕ
ФОРМЫ СИЛЛОГИЗМОВ, КОТОРЫЕ МОЖНО
СОСТАВИТЬ ИЗ
РАССУЖДЕНИЙ ВИДА:- «Все А суть В»
- «Некоторые А суть В»
- «Все А не суть В»
«Некоторые А не суть В»
Логика, основанная на теории
силлогизмов называется классической.
Слайд 9Декарт Рене
(1596-1650, фр. философ, математик)
РЕКОМЕНДОВАЛ В ЛОГИКЕ ИСПОЛЬЗОВАТЬ
МАТЕМАТИЧЕСКИЕ МЕТОДЫ.
Слайд 10Лейбниц Г.В.
(1646-1716, нем. ученый и математик)
Предложил использовать в
логике математическую символику и впервые высказал мысль о возможности применения
в ней двоичной системы счисления.Логика обретает символьный язык, конкретность законов, распространяется за рамки гуманитарных наук.
Слайд 11Джордж Буль
(1815-1864, анл.) - основоположник мат. логики.
1847 г. –Джордж
Буль в работе «Математический анализ логики» изложил основы булевой алгебры.
РАЗРАБОТАЛ АЛФАВИТ, ОРФОГРАФИЮ И ГРАММАТИКУ.
1815 – 1864 гг. благодаря трудам математика Дж. Буля появился раздел математической логики, получивший название алгебры логики или булевой алгебры.
Слайд 13Логика оказала влияние на развитие математики, прежде всего теории множеств,
функциональных систем, алгоритмов, рекурсивных функций.
3) В гуманитарных науках
(логика, криминалистика).
2)
Математическая логика является средством для изучения деятельности мозга - для решения этой самой важной проблемы биологии и науки вообще.
Слайд 141938 г. – американский математик и инженер Клод Шеннон связал
Булеву алгебру (аппарат математической логики), двоичную систему кодирования и релейно-контактные
переключательные схемы, заложив основы будущих ЭВМ.4) Идеи и аппарат логики используется в кибернетике, ВТ и электротехнике (построены компьютеры на основе законов математической
логики).
Слайд 155) Идеи и аппарат логики используется в программировании, базах данных
и экспертных системах.
PROLOG – язык логического программирования
Слайд 17ДИЗЪЮНКЦИЯ
(ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)
СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В В
ОДНО С ПОМОЩЬЮ СОЮЗА «ИЛИ»,
УПОТРЕБЛЯЕМОГО В НЕИСКЛЮЧАЮЩЕМ ВИДЕ.
ОПРЕДЕЛЕНИЕ:
ДИЗЪЮНКЦИЯ
ДВУХ ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ ЛОЖНА ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОБА ВЫСКАЗЫВАНИЯ ЛОЖНЫ.
Слайд 19КОНЪЮНКЦИЯ
(ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) -
Определение:
КОНЪЮНКЦИЯ ДВУХ
ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ
ИСТИННА ТОГДА
И ТОЛЬКО ТОГДА,
КОГДА ОБА ВЫСКАЗЫВАНИЯ
ИСТИННЫ.
Слайд 21ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ
«ЕСЛИ . . . , ТО
. . .»
Определение:
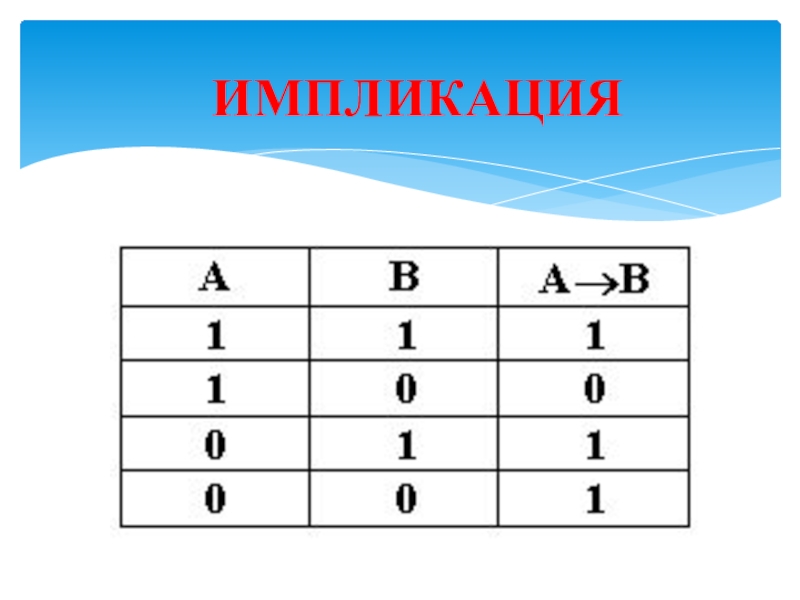
ИМПЛИКАЦИЯ ВЫСКАЗЫВАНИЙ
ЛОЖНА ЛИШЬ В СЛУЧАЕ, КОГДА
А ИСТИННО, А В ЛОЖНО.
ИМПЛИКАЦИЯ
Слайд 23ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ТОГДА И ТОЛЬКО ТОГДА, КОГДА …»
Определение:
ЭКВИВАЛЕНЦИЯ ДВУХ
ВЫСКАЗЫВАНИЙ ИСТИННА В ТОМ И ТОЛЬКО ТОМ СЛУЧАЕ,
КОГДА ОБА ЭТИ ВЫСКАЗЫВАНИЯ ИСТИННЫ ИЛИ ЛОЖНЫ.
ЭКВИВАЛЕНЦИЯ
Слайд 32СОСТАВЬТЕ ВЫРАЖЕНИЕ В 7 ДЕЙСТВИЙ С ИСПОЛЬЗОВАНИЕМ ИЗВЕСТНЫХ ВАМ ЛОГИЧЕСКИХ
ОПЕРАЦИЙ И ЗАПИШИТЕ ДЛЯ НЕЕ ТАБЛИЦУ ИСТЕННОСТИ.
ВЫПОЛНИТЕ ЗАДАНИЕ:
