Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Американский стандарт блочного шифрования Rijndael
Содержание
- 1. Американский стандарт блочного шифрования Rijndael
- 2. Второго октября 2000 года департамент
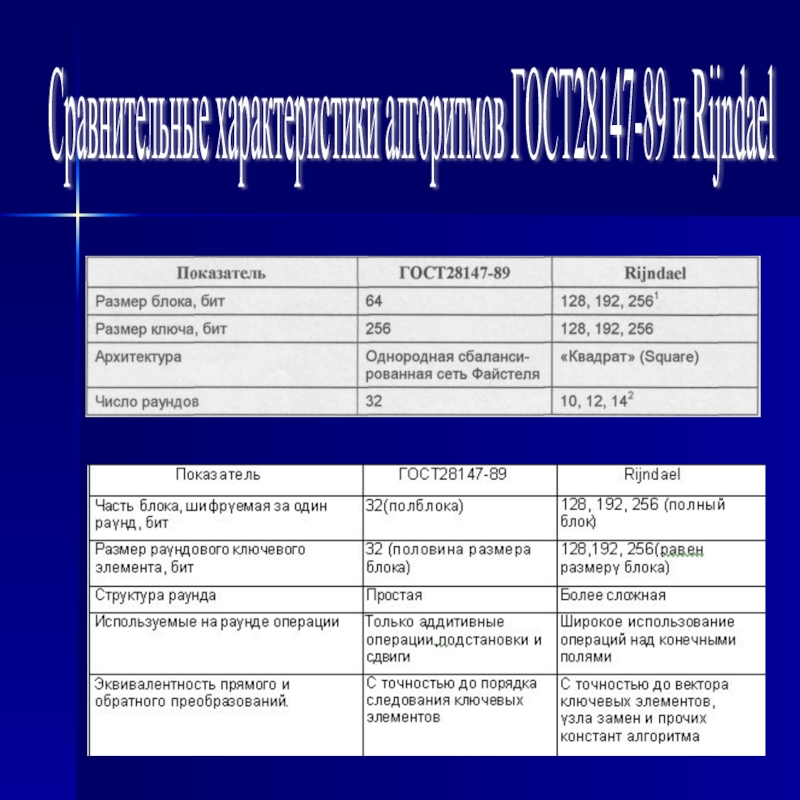
- 3. Сравнительные характеристики алгоритмов ГОСТ28147-89 и Rijndael
- 4. Сравнение общих архитектурных принципов Криптоалгоритм ГОСТ28147-89, как
- 5. Сравнение общих архитектурных принципов
- 6. Общая схема алгоритма Каждый раунд заключается в
- 7. Функция нелинейного преобразования байтовая подстановка - каждый
- 8. Сравнение раундов шифрования
- 9. Эквивалентность прямого и обратного преобразований Шифр Rijndael
- 10. Произведем следующие преобразования: Операция побайтовой замены (S)
- 11. После преобразований Алгоритмическая структура прямого и обратного преобразований идентична
- 12. Процедуры зашифрования и расшифрования различаются: в обратном
- 13. Выработка ключевых элементов Существуют два алгоритма генерации
- 14. Первое 4-байтовое слово вырабатывается с использованием сложного
- 15. Выбор узлов замен и констант При конструировании
- 16. Операция байтовой замены Операция байтовой замены в
- 17. Выводы: При конструировании шифра Rijndael широко использован
- 18. Скачать презентанцию
Слайды и текст этой презентации
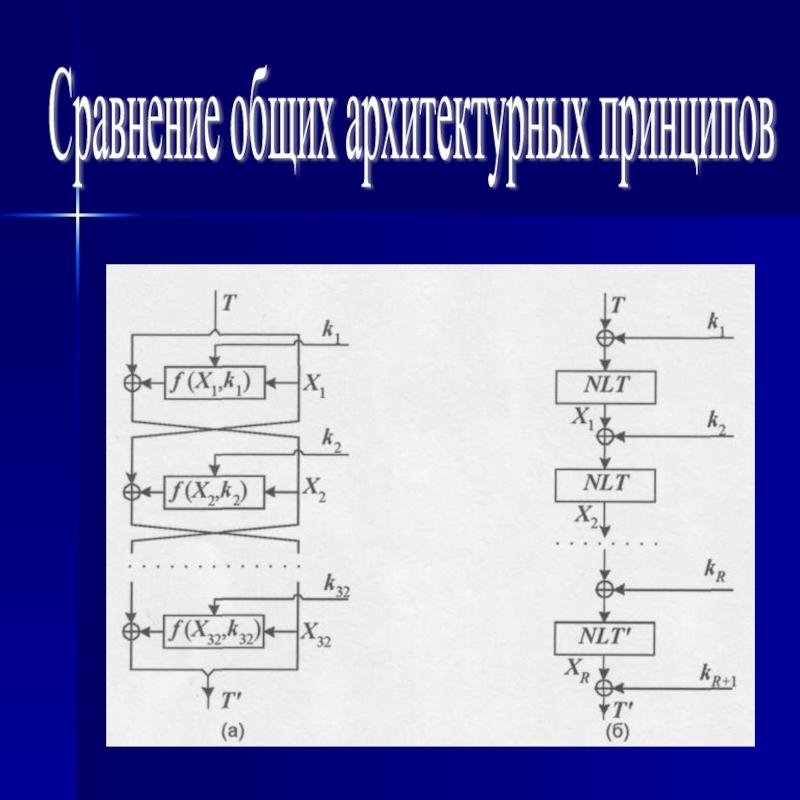
Слайд 4Сравнение общих архитектурных принципов
Криптоалгоритм ГОСТ28147-89, как и большинство шифров
«первого поколения», разрабатывавшихся в 70-е годы и в первой половине
80-х, базируется на архитектуре «сбалансированная сеть Фейстеля»Шифр Rijndael имеет архитектуру «квадрат» (Square).
Эта архитектура базируется на прямых преобразованиях шифруемого блока, который представляется в форме матрицы байтов. Зашифрование также состоит из серии однотипных шагов, раундов, однако на каждом раунде блок преобразуется как единое целое и не остается неизменных частей блока.
Таким образом, за раунд шифруется полный блок, следовательно, для обеспечения сопоставимой сложности и нелинейности преобразования таких шагов требуется вдвое меньше по сравнению с сетью Файстеля.
Слайд 6Общая схема алгоритма
Каждый раунд заключается в побитовом сложении по
модулю 2 текущего состояния шифруемого блока и ключевого элемента раунда,
за которым следует сложное нелинейное преобразование блока, сконструированное из трех более простых преобразований.В Rijndael шифруемый блок и его промежуточные состояния в ходе преобразования представляются в виде матрицы байтов 4×n, где
n =4, 6, 8 в зависимости от размера блока.
Слайд 7Функция нелинейного преобразования
байтовая подстановка - каждый байт преобразуемого блока
заменяется новым значением, извлекаемым из общего для всех байтов матрицы вектора
замены;побайтовый циклический сдвиг в строках матрицы: первая строка остается неизменной, вторая строка циклически сдвигается влево на один байт, третья и четвертая строка циклически сдвигаются влево соответственно на 2 и 3 байта;
матричное умножение - полученная на предыдущем шаге матрица умножается слева на матрицу-циркулянт размера 4x4:
Слайд 9Эквивалентность прямого и обратного преобразований
Шифр Rijndael построен на базе
прямых преобразований. Как и для всех подобных алгоритмов, обратное преобразование
строится из обращений шагов прямого преобразования, применяемых в обратном порядке.Слайд 10Произведем следующие преобразования:
Операция побайтовой замены (S) коммутативна с процедурой
побайтового сдвига строк матрицы:
Кроме того, согласно правилам матричной алгебры по
закону ассоциативности можно также поменять порядок побитового прибавления ключа по модулю два и умножения на матрицу:Слайд 12Процедуры зашифрования и расшифрования различаются:
в обратном преобразовании используется вектор
замен, обратный в операционном смысле вектору замен прямого преобразования;
в обратном
преобразовании число байтов, на которые сдвигается каждая строка матрицы данных в операции построчного байтового сдвига другое;в обратном преобразовании в шаге матричного умножения блок данных умножается слева на матрицу, обратную той, что используется при прямом преобразовании;
в обратном преобразовании ключевые элементы используются в обратном порядке, и, кроме того, все элементы за исключением первого и последнего, должны быть умножены слева на матрицу М-1.
Слайд 13Выработка ключевых элементов
Существуют два алгоритма генерации последовательности ключевых элементов
- для ключа размером 128/192 бита и для ключа размером
256 бит.Ключ и ключевая последовательность представляются в виде векторов 4-х байтовых слов, и начальный участок последовательности заполняется словами из ключа, точно так же, как в ГОСТе. Последующие слова ключевой последовательности вырабатываются по рекуррентному соотношению группами, кратными размеру ключа.
Слайд 14Первое 4-байтовое слово вырабатывается с использованием сложного нелинейного преобразования, остальные
- по простому линейному соотношению:
где Nk - число 32-битовых слов
в ключе (4 или 6) G(w) - нелинейное преобразование 32-битовых слов - включает байтовый сдвиг, побайтовую подстановку по вектору замен и побитовое сложение по модулю 2 с вектором, зависящим от номера вырабатываемой группы элементов:
P(i/Nk) - 4-байтовое слово, конструируемое особым образом и не зависящее от ключа.
Полученные из описанного выше потока 4-байтовые слова группируются в ключевые элементы необходимого размера, равного размеру шифруемого блока, и используются на раундах шифрования.
Слайд 15Выбор узлов замен и констант
При конструировании узлов замен помимо
тривиальных требований обратимости и простоты описания были приняты во внимание
следующие соображения:• минимизация самой большой по величине характеристики корреляции между линейными комбинациями входных и выходных битов (определяет устойчивость к линейному криптоанализу);
минимизация наибольшего нетривиального значения в таблице EXOR (определяет устойчивость к дифференциальному криптоанализу);
сложность алгебраического выражения, описывающего узел, в GF(28).
Слайд 16Операция байтовой замены
Операция байтовой замены в алгоритме Rijndael описывается
следующим уравнением:
Это преобразование начинается с мультипликативной инверсии заменяемого байта в
описанном выше конечном поле GF(28), - значение 00 при этом меняется на самого себя, затем результат подвергается аффинному преобразованию. Полиномы этого преобразования выбраны таким образом, чтобы у итогового отображения отсутствовали точки неподвижности (S(X)=X) и «антинеподвижности» (S(X) = ~X). Здесь знаком «~» обозначена операция побитового инвертирования.
Слайд 17Выводы:
При конструировании шифра Rijndael широко использован алгебраический подход.
Это
касается главным образом двух основных преобразований шифра - байтовой замены
и операции перемешивания столбцов матрицы данных посредством ее умножения слева на матрицу М.По оценкам разработчиков шифра Rijndael, уже на четырех раундах шифрования этот алгоритм приобретает достаточную устойчивость к различным видам криптоанализа.
Теоретической границей, за которой линейный и дифференциальный виды криптоанализа теряют смысл, является рубеж в 6-8 раундов в зависимости от размера блока.
Согласно спецификации, в шифре предусмотрено 10-14 раундов.
Следовательно, шифр Rijndael устойчив к указанным видам криптоанализа с определенным запасом.