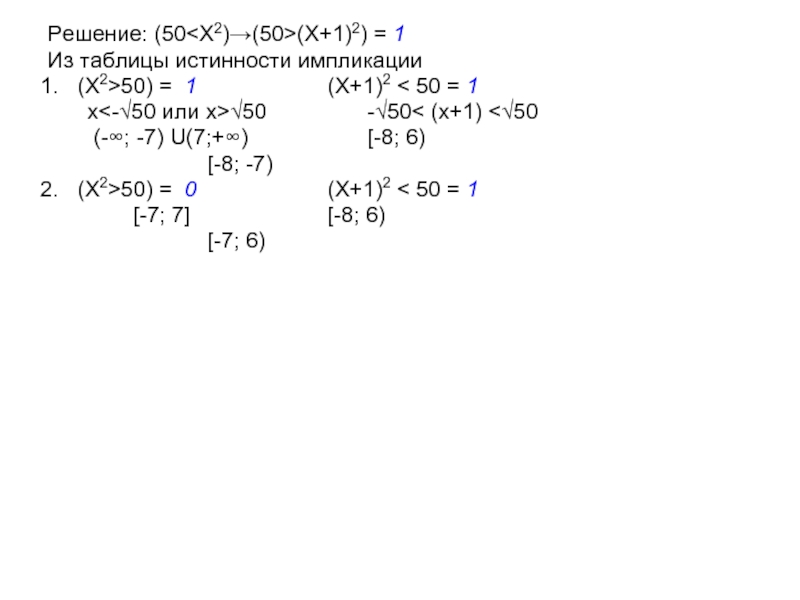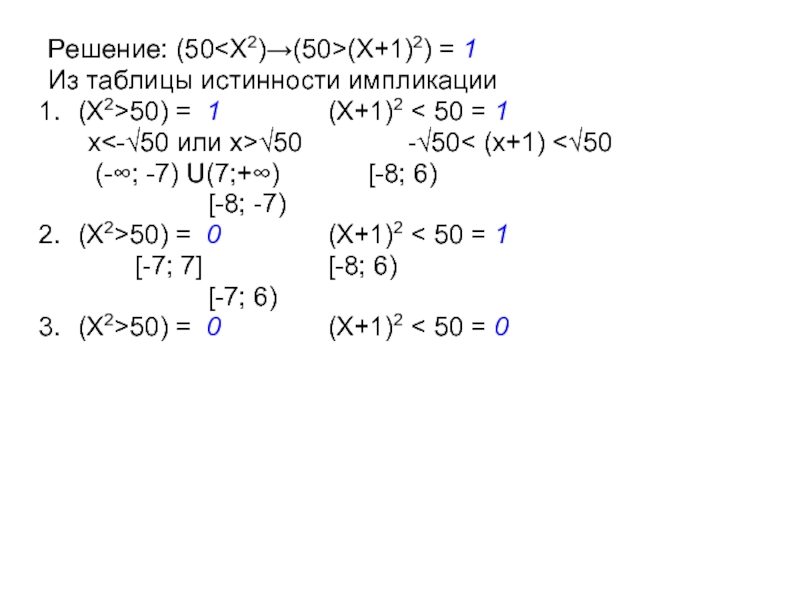Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ по информатике
Содержание
- 1. ЕГЭ по информатике
- 2. Основы логикиЗнание символикиЗнание таблиц истинности основных логических
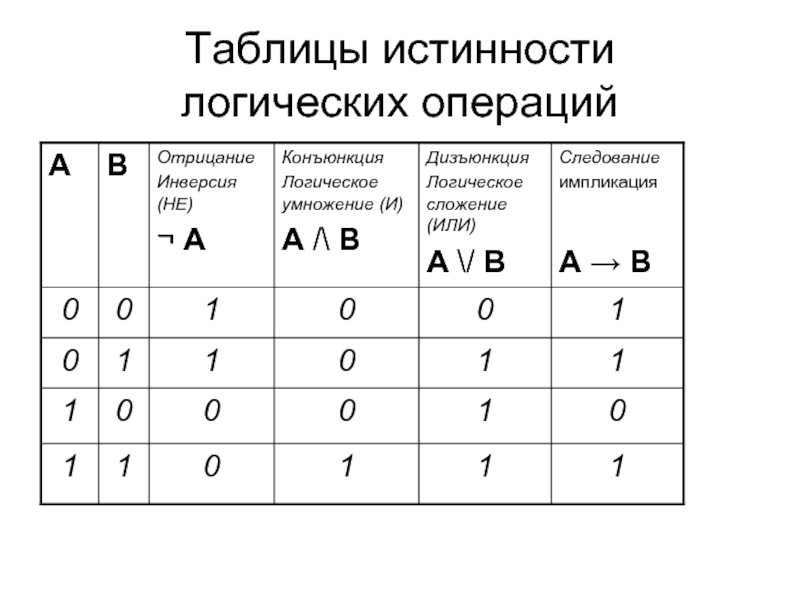
- 3. Таблицы истинности логических операций
- 4. Основы логикиПример 1. Для какого из указанных
- 5. Пример 2. Укажите, какое логическое выражение равносильно
- 6. Пример 2. Укажите, какое логическое выражение равносильно
- 7. Пример 2. Укажите, какое логическое выражение равносильно
- 8. Пример 2. Укажите, какое логическое выражение равносильно
- 9. Пример 3. Сколько различных решений имеет уравнение
- 10. ((K /\L) –> (L /\ M \/
- 11. ((K /\L) –> (L /\ M \/
- 12. ((K /\L) –> (L /\ M \/
- 13. ((K /\L) –> (L /\ M \/
- 14. ((K /\L) –> (L /\ M \/
- 15. Пример 4. Для какого из указанных значений
- 16. Пример 4. Для какого из указанных значений
- 17. Пример 4. Для какого из указанных значений
- 18. Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) → (X>3))?
- 19. Пример 5. Для каких значений X истинно
- 20. Пример 5. Для каких значений X истинно
- 21. Пример 5. Для каких значений X истинно
- 22. Пример 5. Для каких значений X истинно
- 23. Пример 6. Каково наибольшее ЦЕЛОЕ число X,
- 24. Пример 6. Каково наибольшее ЦЕЛОЕ число X,
- 25. Пример 6. Каково наибольшее ЦЕЛОЕ число X,
- 26. Пример 6. Каково наибольшее ЦЕЛОЕ число X,
- 27. Пример 6. Каково наибольшее ЦЕЛОЕ число X,
- 28. Пример 6. Каково наибольшее ЦЕЛОЕ число X,
- 29. Пример 6. Каково наибольшее ЦЕЛОЕ число X,
- 30. Пример 7. Каково наибольшее целое число X,
- 31. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 32. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 33. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 34. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 35. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 36. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 37. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 38. Решение: (50(X+1)2) = 1Из таблицы истинности импликации(X2>50)
- 39. Проверка.(50(X+1)2) при x= 7(50(7+1)2) (5064) истина при x= -8(50(-8+1)2) (5049) истина
- 40. Пример 8. Пончик, Ленчик и Батончик нашли
- 41. Простые высказыванияП – Пончик утаил кладЛ -
- 42. Леньчик: Пончик этого не делал(¬П). Виноват Батончик
- 43. Следствие установило, что один оба раза солгал,
- 44. Пример 9. Синоптик объявляет погоду на завтра
- 45. Запишем высказыванияЕсли не будет ветра, то будет
- 46. Запишем высказыванияЕсли не будет ветра, то будет
- 47. Запишем высказыванияЕсли не будет ветра, то будет
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. Простые высказыванияВ – ветерП – пасмурноД -
- 54. Пример 10.
- 55. Решение.Дом 1 Дом 2 Дом 3 Дом 4
- 56. Решение.Слесарь живет левее Учителя С
- 57. Решение.Дом 1 Дом 2 Дом 3 Дом
- 58. Решение.Дом 1 Дом 2 Дом 3 Дом 4Слесарь живет левее Учителя С У
- 59. Решение.Дом 1 Дом 2 Дом 3 Дом
- 60. Решение.Дом 1 Дом 2 Дом 3 Дом
- 61. Решение.Дом 1 Дом 2 Дом 3 Дом 46. Андрей живет рядом с Учителем
- 62. Решение.Дом 1 Дом 2 Дом 3 Дом 47. Иван живет левее Парикмахера
- 63. Решение.Дом 1 Дом 2 Дом 3 Дом 47. Иван живет через дом от Андрея
- 64. Решение.Дом 1 Дом 2 Дом 3 Дом 4Ответ: СИ, УБ, ПА, ВМ
- 65. Скачать презентанцию
Основы логикиЗнание символикиЗнание таблиц истинности основных логических операций (инверсия, конъюнкция, дизъюнкция), а также импликацииЗнание и применение основных законов логики
Слайды и текст этой презентации
Слайд 2Основы логики
Знание символики
Знание таблиц истинности основных логических операций (инверсия, конъюнкция,
дизъюнкция), а также импликации
Слайд 4Основы логики
Пример 1. Для какого из указанных значений X истинно
высказывание ¬ ((X >2) → (X>3))?
1)x=1 2) x= 2 3) x= 3 4)
x= 4Слайд 5Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/
¬ B \/ C)
1) ¬A \/ B \/ ¬C
2)
A /\ ¬B /\ C 3)¬A \/ ¬B \/ ¬C
4) ¬A /\ B /\ ¬C
Слайд 6Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/
¬ B \/ C)
1) ¬A \/ B \/ ¬C 2)
A /\ ¬B /\ C 3)¬A \/ ¬B \/ ¬C 4) ¬A /\ B /\ ¬C
Решение: ¬(A \/ B)= ¬A /\ ¬B
¬(¬ A) = A
Слайд 7Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/
¬ B \/ C)
1) ¬A \/ B \/ ¬C 2)
A /\ ¬B /\ C 3)¬A \/ ¬B \/ ¬C 4) ¬A /\ B /\ ¬C
Решение: ¬(A \/ B)= ¬A /\ ¬B
¬(¬ A) = A
¬(A \/ ¬ B \/ C) = ¬A /\ ¬(¬B) /\ ¬C =
Слайд 8Пример 2. Укажите, какое логическое выражение равносильно выражению ¬(A \/
¬ B \/ C)
1) ¬A \/ B \/ ¬C 2)
A /\ ¬B /\ C 3)¬A \/ ¬B \/ ¬C 4) ¬A /\ B /\ ¬C
Решение: ¬(A \/ B)= ¬A /\ ¬B
¬(¬ A) = A
¬(A \/ ¬ B \/ C) = ¬A /\ ¬(¬B) /\ ¬C =
¬A /\ B /\ ¬C
Ответ 4
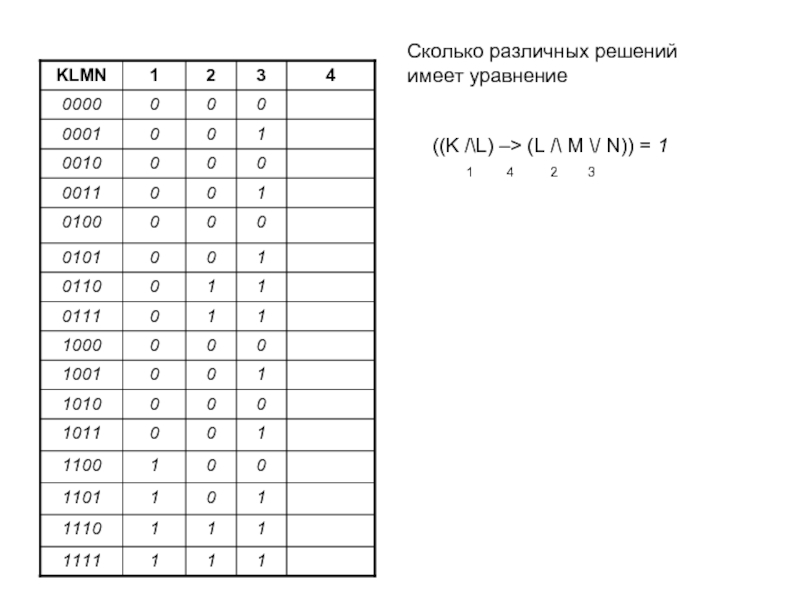
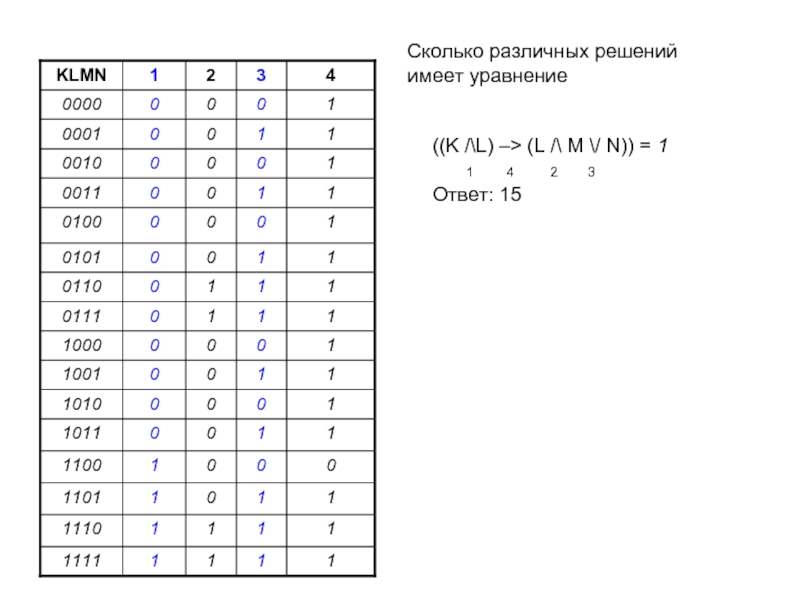
Слайд 9Пример 3. Сколько различных решений имеет уравнение ((K /\L) –>
(L /\ M \/ N)) = 1, где K, L,
M, N – логические переменные?Слайд 15Пример 4. Для какого из указанных значений X истинно высказывание ¬
((X>2) → (X>3))?
1)x=1 2) x= 2 3) x= 3 4) x= 4
Решение:
¬
((X>2) → (X>3)) = 1(X>2) → (X>3) = 0
Слайд 16Пример 4. Для какого из указанных значений X истинно высказывание ¬
((X>2) → (X>3))?
1)x=1 2) x= 2 3) x= 3 4) x= 4
Решение:
¬
((X>2) → (X>3)) = 1(X>2) → (X>3) = 0
Из таблицы истинности импликации
1 → 0 = 0
Слайд 17Пример 4. Для какого из указанных значений X истинно высказывание ¬
((X>2) → (X>3))?
1)x=1 2) x= 2 3) x= 3 4) x= 4
Решение:
¬
((X>2) → (X>3)) = 1(X>2) → (X>3) = 0
Из таблицы истинности импликации 1 → 0 = 0
Ответ: 3) x= 3
Слайд 19Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) →
(X>3))?
Решение:
¬ ((X>2) → (X>3)) = 1
(X>2) → (X>3) = 0
Слайд 20Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) →
(X>3))?
Решение:
¬ ((X>2) → (X>3)) = 1
(X>2) → (X>3) = 0
1→
0 = 0Слайд 21Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) →
(X>3))?
Решение:
¬ ((X>2) → (X>3)) = 1
(X>2) → (X>3) = 0
1
→ 0 = 0X >2 и X<=3
Слайд 22Пример 5. Для каких значений X истинно высказывание ¬ ((X>2) →
(X>3))?
Решение:
¬ ((X>2) → (X>3)) = 1
(X>2) → (X>3) = 0
1
→ 0 = 0X >2 и X<=3
(2;3]
Слайд 24Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно
(90 < X·X) → (X < (X – 1)) ?
Решение:
(90 < X2) → (X < (X – 1)) = 1Слайд 25Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно
(90 < X·X) → (X < (X – 1)) ?
Решение:
(90 < X2) → (X < (X – 1)) = 1Из таблицы истинности импликации
1→ 1 = 1
0 → 1 = 1
0 → 0 = 1
Слайд 26Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно
(90 < X·X) → (X < (X – 1)) ?
Решение:
(90 < X2) → (X < (X – 1)) = 1Из таблицы истинности импликации
1 → 1 = 1
0 → 1 = 1
0 → 0 = 1
X < (X – 1) = 0 для всех X,
следовательно (90 < X2) = 0
Слайд 27Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно
(90 < X·X) → (X < (X – 1)) ?
Решение:
(90 < X2) → (X < (X – 1)) = 1Из таблицы истинности импликации
1 → 1 = 1
0 → 1 = 1
0 → 0 = 1
X < (X – 1) = 0 для всех X,
следовательно (90 < X2) = 0
если 90 =>X2
Слайд 28Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно
(90 < X·X) → (X < (X – 1)) ?
Решение:
(90 < X2) → (X < (X – 1)) = 1Из таблицы истинности импликации
1 → 1 = 1
0 → 1 = 1
0 → 0 = 1
X < (X – 1) = 0 для всех X,
следовательно (90 < X2) = 0
если 90 =>X2
-√90<=x<=+√90
Слайд 29Пример 6. Каково наибольшее ЦЕЛОЕ число X, при котором истинно
(90 < X·X) → (X < (X – 1)) ?
Решение:
(90 < X2) → (X < (X – 1)) = 1Из таблицы истинности импликации
1 → 1 = 1
0 → 1 = 1
0 → 0 = 1
X < (X – 1) = 0 для всех X,
следовательно (90 < X2) = 0
если 90 =>X2
-√90<=x<=+√90
Ответ: x = 9
Слайд 30Пример 7. Каково наибольшее целое число X, при котором истинно
высказывание
(50(X+1)·(X+1))
Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
1 →
1 = 10 → 1 = 1
0 → 0 = 1
Слайд 31Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
(X2>50) = 0 (X+1)2 < 50
= 1(X2>50) = 0 (X+1)2 < 50 = 0
Слайд 32Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
x√50 -√50< (x+1)
Слайд 33Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
x√50 -√50< (x+1)
<√50(-∞; -7)U(7;+∞) (-8; 6)
Слайд 34Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
x√50 -√50< (x+1)
(-∞; -7) U(7;+∞) [-8; 6)[-8; -7)
Слайд 35Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
x√50
-√50< (x+1) <√50(-∞; -7) U(7;+∞) [-8; 6)
[-8; -7)
(X2>50) = 0 (X+1)2 < 50 = 1
Слайд 36Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
x√50 -√50< (x+1)
(-∞; -7) U(7;+∞) [-8; 6)[-8; -7)
(X2>50) = 0 (X+1)2 < 50 = 1
[-7; 7] [-8; 6)
[-7; 6)
Слайд 37Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
x√50 -√50< (x+1)
(-∞; -7) U(7;+∞) [-8; 6)[-8; -7)
(X2>50) = 0 (X+1)2 < 50 = 1
[-7; 7] [-8; 6)
[-7; 6)
(X2>50) = 0 (X+1)2 < 50 = 0
Слайд 38Решение: (50(X+1)2) = 1
Из таблицы истинности импликации
(X2>50) = 1 (X+1)2
< 50 = 1
x√50 -√50< (x+1)
(-∞; -7) U(7;+∞) [-8; 6)[-8; -7)
(X2>50) = 0 (X+1)2 < 50 = 1
X2<=50
-√50<= x<=√50 -√50< (x+1) <√50
[-7; 7] [-8; 6)
[-7; 6)
(X2>50) = 0 (X+1)2 < 50 = 0
[-7; 7] (-∞; -8) U[6;+∞)
[6;7]
Ответ: наибольшее целое x=7
Слайд 40Пример 8. Пончик, Ленчик и Батончик нашли клад. Один из
них этот клад утаил. На следствии они сделали следующие заявления.
Леньчик: Пончик этого не делал. Виноват Батончик.
Пончик: Батончик этого не делал. Это сделал Ленчик.
Батончик: Пончик врет. Леньчик не виноват.
Следствие установило, что один оба раза солгал, а остальные говорили правду. Кто утаил клад?
Слайд 41Простые высказывания
П – Пончик утаил клад
Л - Ленчик утаил клад
Б
- Батончик утаил клад
Высказывания
Леньчик: Пончик этого не делал(¬П). Виноват Батончик
(Б). Пончик: Батончик этого не делал(¬Б). Это сделал Ленчик (Л).
Батончик: Пончик врет ¬(¬Б/\ Л) . Леньчик не виноват (¬Л)
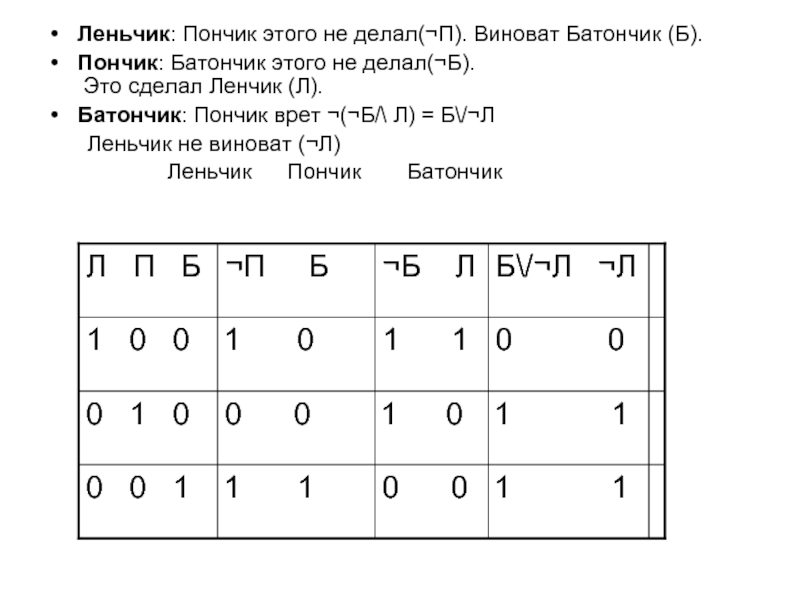
Слайд 42Леньчик: Пончик этого не делал(¬П). Виноват Батончик (Б).
Пончик: Батончик
этого не делал(¬Б).
Это сделал Ленчик (Л).
Батончик: Пончик врет
¬(¬Б/\ Л) = Б\/¬ЛЛеньчик не виноват (¬Л)
Леньчик Пончик Батончик
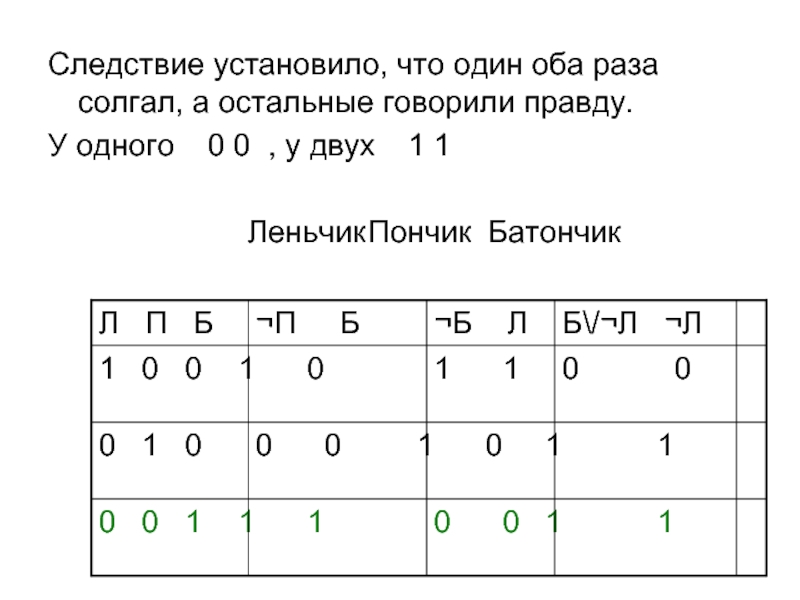
Слайд 43Следствие установило, что один оба раза солгал, а остальные говорили
правду.
У одного 0 0 , у двух 1 1
Леньчик Пончик БатончикСлайд 44Пример 9. Синоптик объявляет погоду на завтра и утверждает следующее:
Если
не будет ветра, то будет пасмурная погода без дождя
Если будет
дождь, то будет пасмурно и без ветраЕсли будет пасмурно, то будет дождь и не будет ветра
Какая погода будет завтра?
Решение: Выделим простые высказывания
В – ветер
П – пасмурно
Д - дождь
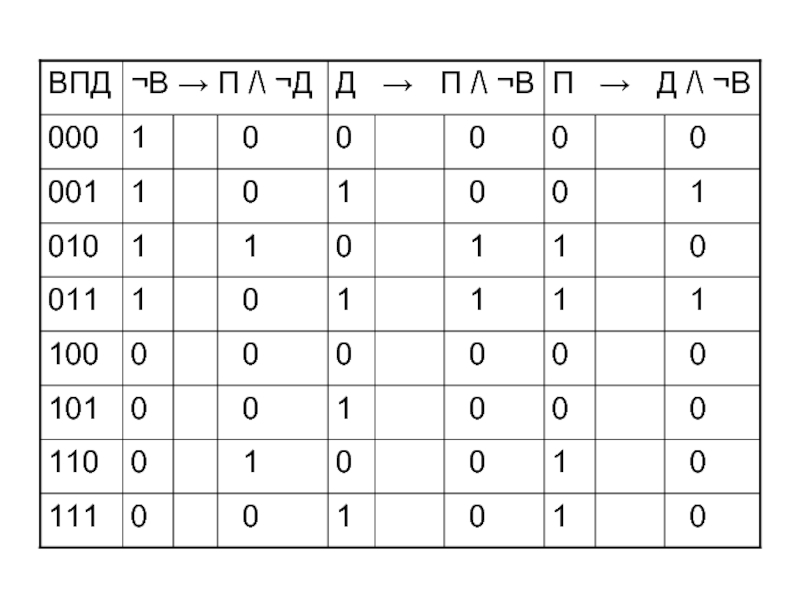
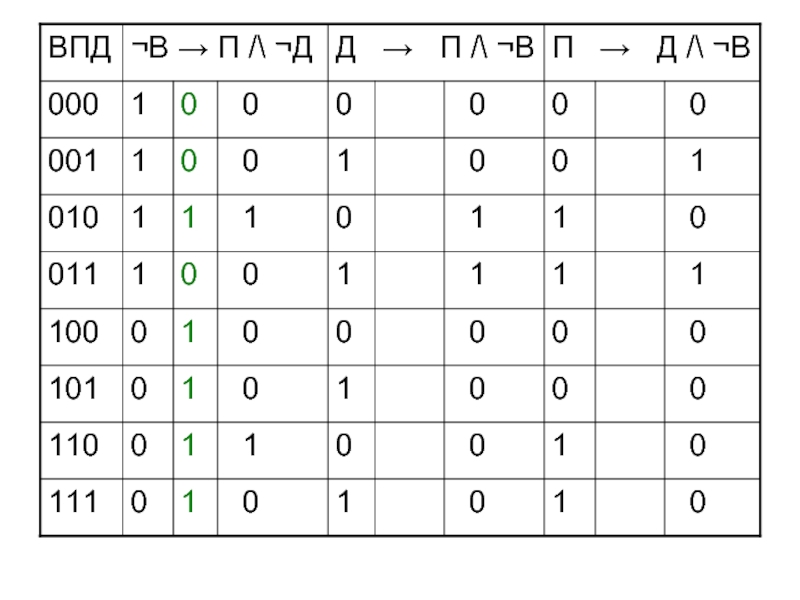
Слайд 46Запишем высказывания
Если не будет ветра, то будет пасмурная погода без
дождя
¬В → П /\ ¬Д
Если будет дождь, то будет
пасмурно и без ветраД → П /\ ¬В
Слайд 47Запишем высказывания
Если не будет ветра, то будет пасмурная погода без
дождя
¬В → П /\ ¬Д
Если будет дождь, то будет
пасмурно и без ветраД → П /\ ¬В
Если будет пасмурно, то будет дождь и не будет ветра
П → Д /\ ¬В
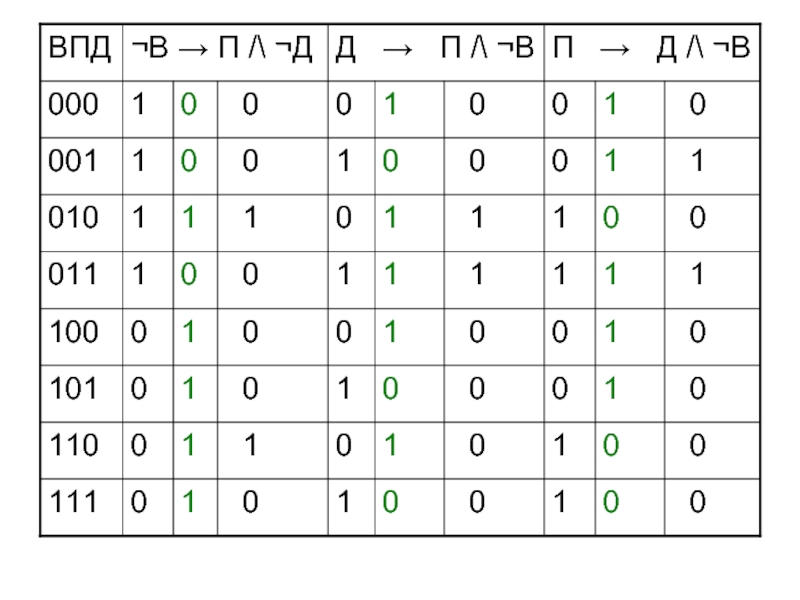
Слайд 53Простые высказывания
В – ветер
П – пасмурно
Д - дождь
В – 1
П – 0 Д – 0
Ответ: погода будет ясная, без
дождя, но ветренаяСлайд 56Решение.
Слесарь живет левее Учителя С У
2.
Парикмахер живет правее Учителя У
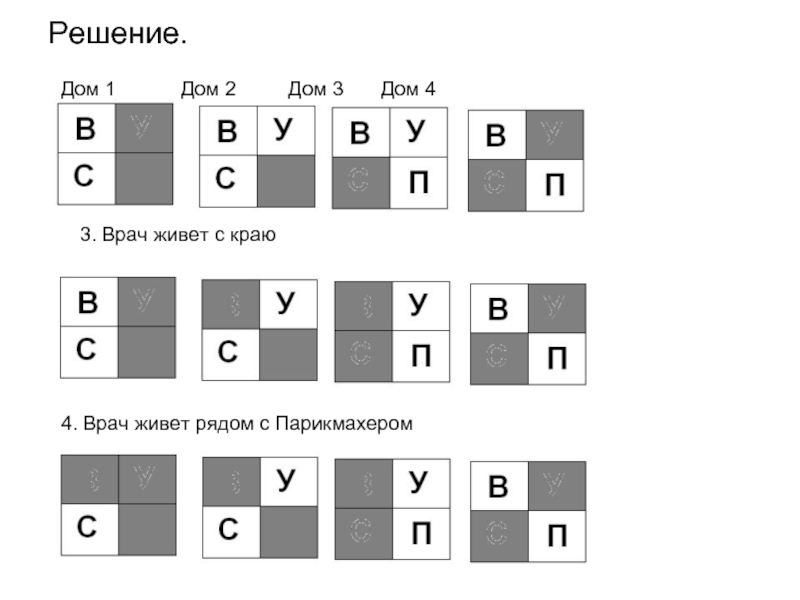
П3. Врач живет с краю
4. Врач живет рядом с Парикмахером
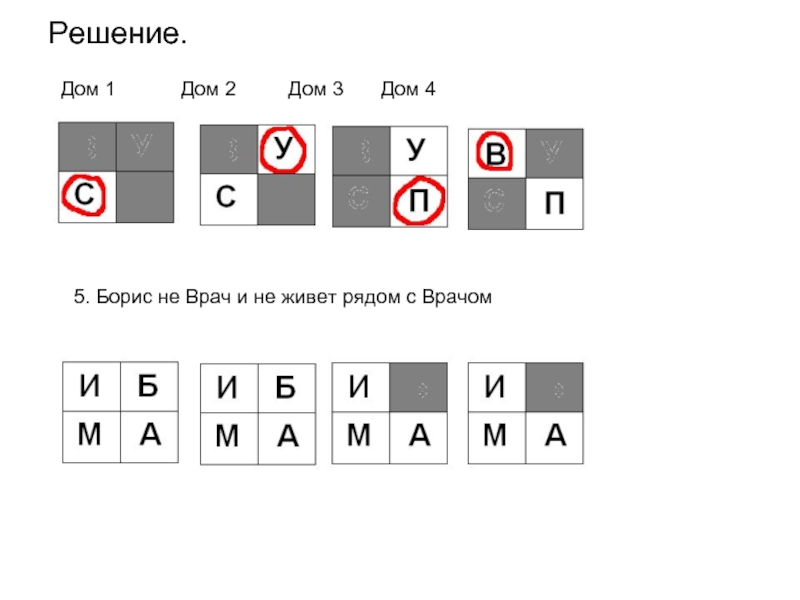
5. Борис не Врач и не живет рядом с Врачом
6. Андрей живет рядом с Учителем
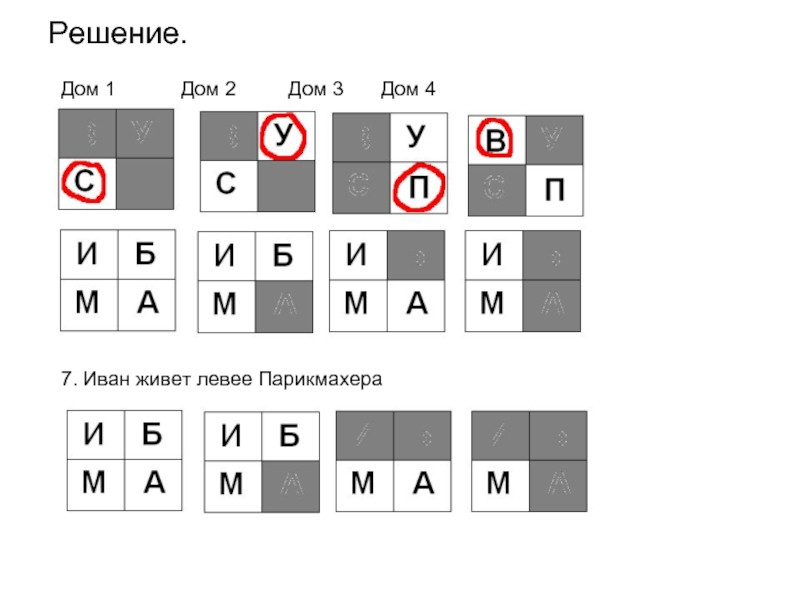
7. Иван живет левее Парикмахера И П
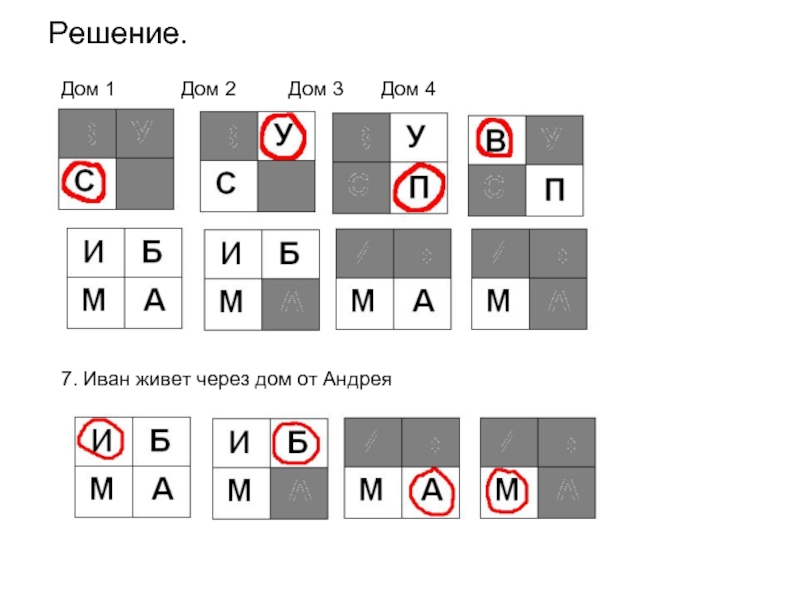
8. Иван живет через дом от Андрея
Слайд 57Решение.
Дом 1 Дом 2 Дом 3 Дом 4
Слесарь живет левее
Учителя С У
2. Парикмахер живет правее Учителя
У П
Теги