по определённым правилам с помощью символов некоторого алфавита, называемых цифрами.
Числа:
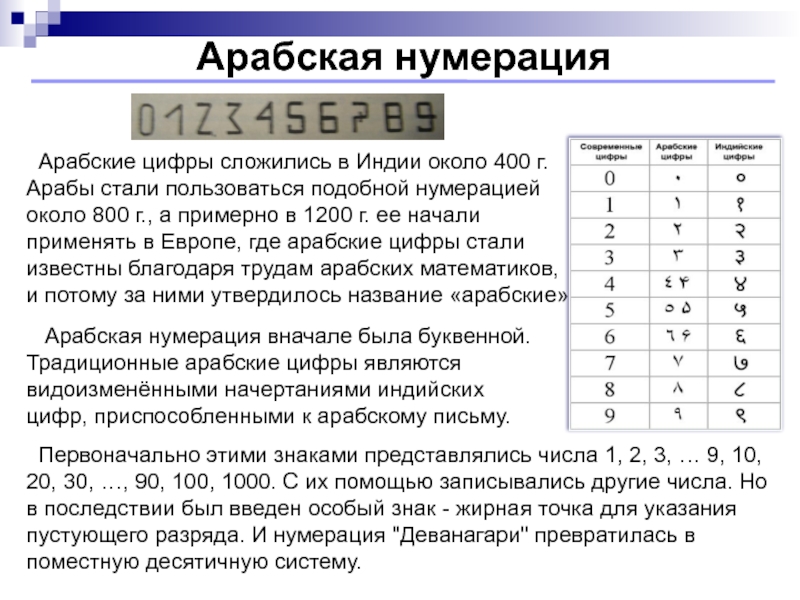
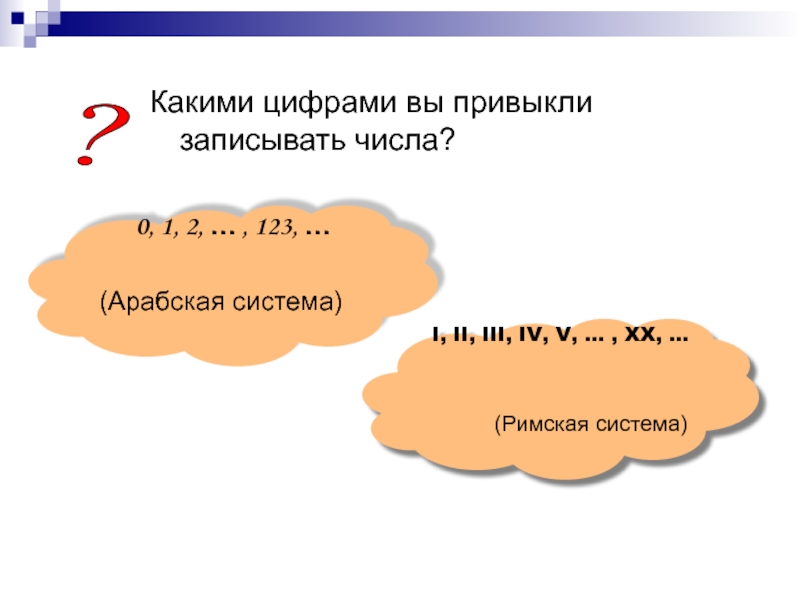
под числом понимается его величина, а не символьная запись. Например, 123, 1010011, CXLЦифры – символы, при помощи которых записывается число. Например, 0, 1, 2, … I, V, X, L, …
Алфавит – это набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
{0, 1}
{0, 1, … , A, B, C, D, E, F}