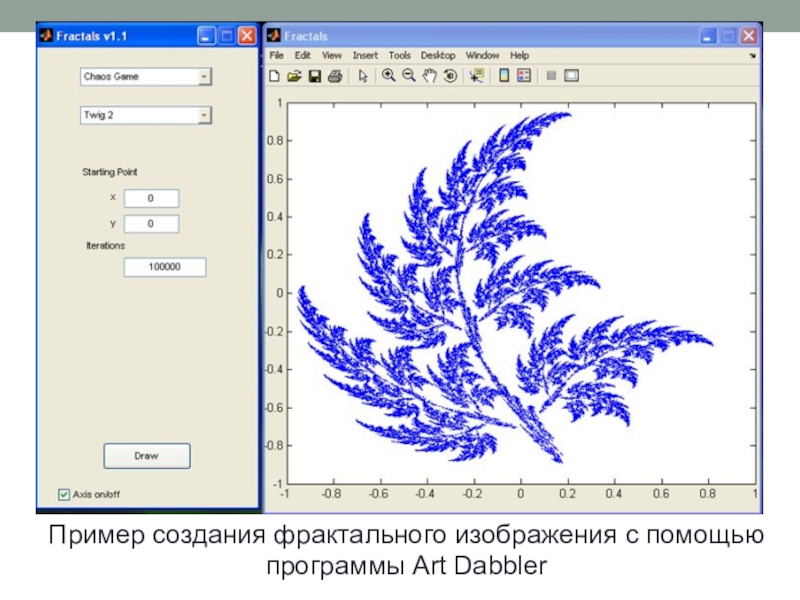
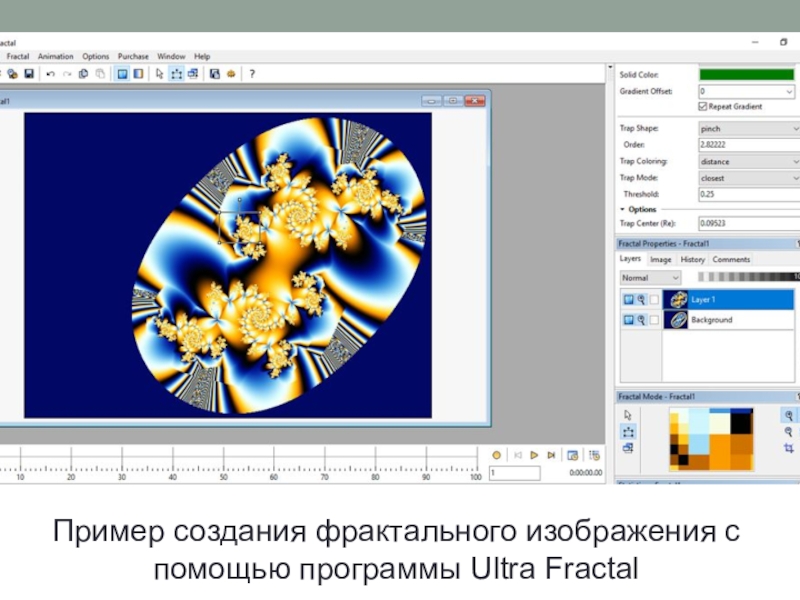
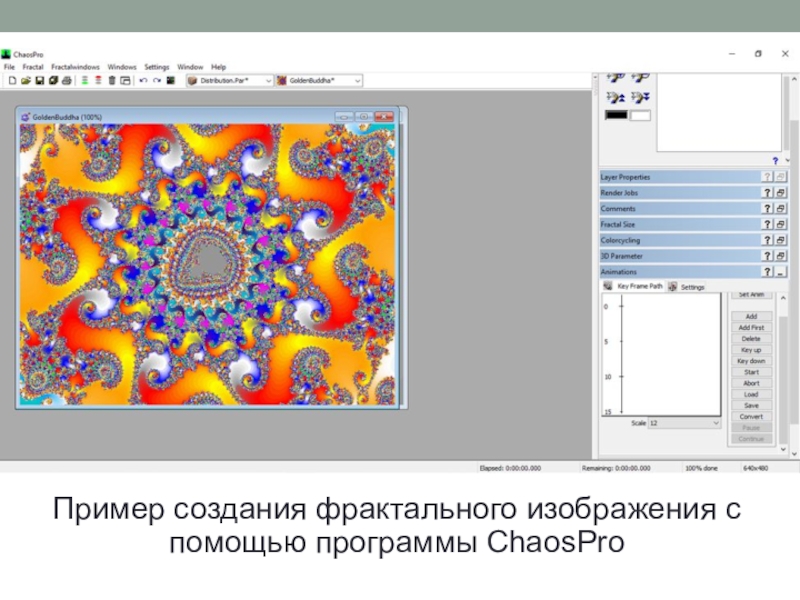
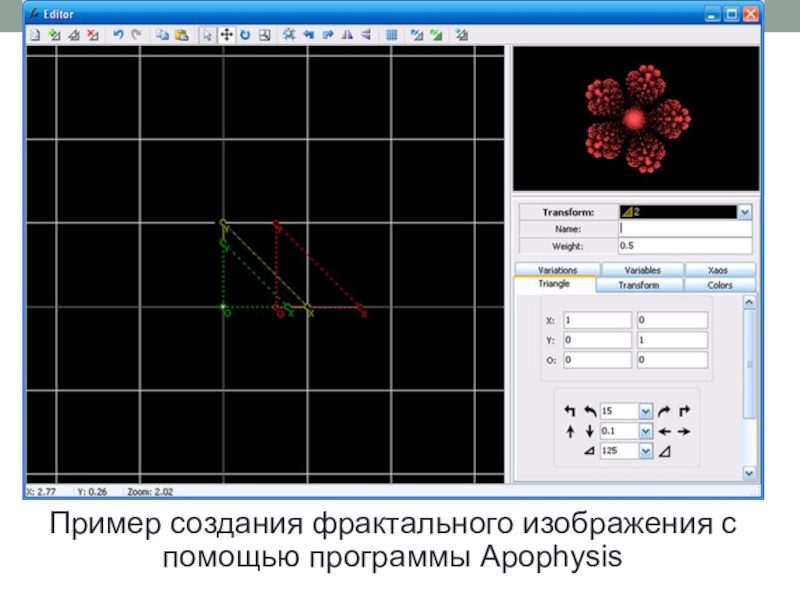
Фрактальная графика в специальных программных средствах

фрактальной геометрии принято связывать с выходом в 1977 году его

книги «Фрактальная геометрия природы».
Фрактал (лат. fractus – дробленый) – это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.

(снежинка Коха)
Кривая Леви
Кривая Гильберта
Ломаная (кривая) дракона (Фрактал Хартера-Хейтуэя)
Множество Кантора
Треугольник Серпинского
Ковер

Серпинского
Дерево Пифагора
Стохастические фракталы
Рукотворные фракталы
Природные фракталы
Детерминированные фракталы
Недетерминированные фракталы

Базовыми элементами фрактальной графики являются сами математические формулы, описывающие линии

и линейные поверхности.
Фрактальная графика не является, строго говоря, частью векторной графики, поскольку широко использует и растровые объекты. Фракталы широко используются в растровых (AdobePhotoshop) и векторных (CorelDraw) редакторах и трехмерной (CorelBryce) графике.

−
М.: «Институт компьютерных исследований», 2002.
2. Федер, Е. Фракталы / Е. Федер.

− М: «Мир», 1991.
3. Шредер, М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая / М. Шредер.− Ижевск: «РХД», 2001.
4. Красота математических поверхностей. – М.: Куб, 2005.
5. Леонтьев, В.П. Новейшая энциклопедия Интернет / В.П.Леонтьев. – М.: ОЛМА-ПРЕСС, 2003.
6. Шляхтина, С. В мире фрактальной графики / С.В.Шляхтина – СПб., Компьютер Price, 2005.
7. http://fb.ru/article/228910/grafika-fraktalnaya-opisanie-primeryi-formatyi-dostoinstva-i-nedostatki
8. https://sites.google.com/site/vidygrafiki/lekcia-po-teme-vidy-grafiki/fraktalnaa-grafika