Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование фракталов в системе Maxima
Содержание
- 1. Моделирование фракталов в системе Maxima
- 2. MaximaMaxima — система работы с символьными и числовыми
- 3. Бенуа Мандельброт
- 4. Слайд 4
- 5. Свойства фракталовОбладает сложной структурой при любом увеличенииЯвляется
- 6. В живой природе:КораллыМорские звезды и ежиМорские раковиныЦветы и растения
- 7. Слайд 7
- 8. Обзор пакета fractals треугольник Серпинского, фракталы
- 9. Функции пакета fractals
- 10. Треугольник Серпинского
- 11. Снежинка Коха
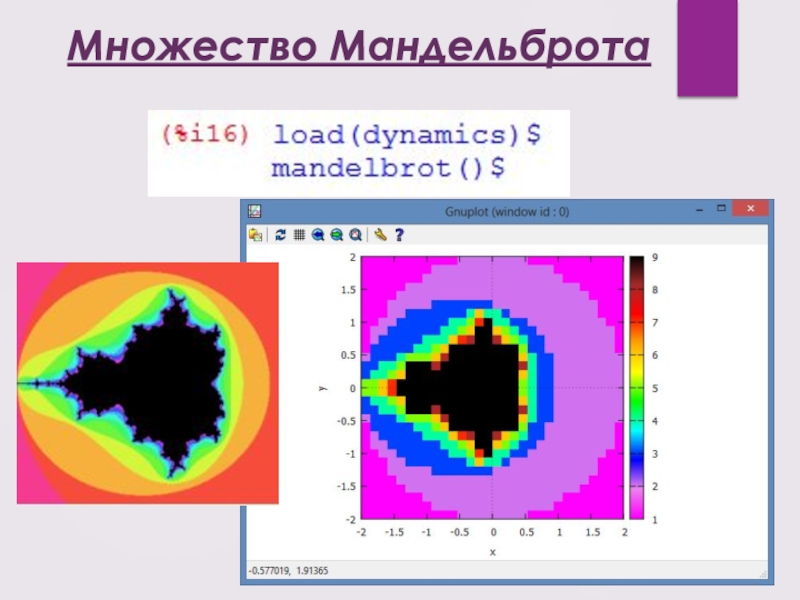
- 12. Множество Мандельброта
- 13. Множество Жюлиа
- 14. Обзор пакета dynamicsпаутинная диаграммабифуркационная диаграммаэволюция орбиты одно-
- 15. Функции пакета dynamics
- 16. «Игра в хаос»
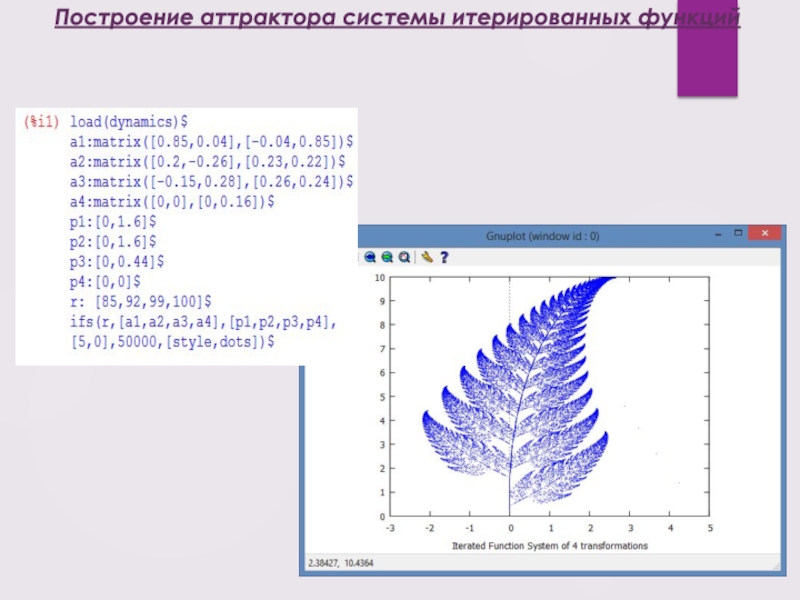
- 17. Построение аттрактора системы итерированных функций
- 18. Множествo Жюлиа
- 19. Множество Мандельброта
- 20. Скачать презентанцию
MaximaMaxima — система работы с символьными и числовыми выражениями, включающая дифференцирование, интегрирование, разложение в ряд, преобразование Лапласа, обыкновенные дифференциальные уравнения, системы линейных уравнений, многочлены, множества, списки, векторы, матрицы и тензоры.
Слайды и текст этой презентации
Слайд 2Maxima
Maxima — система работы с символьными и числовыми выражениями, включающая дифференцирование,
Слайд 5Свойства фракталов
Обладает сложной структурой при любом увеличении
Является (приближенно) самоподобной
Обладает дробной
метрической размерностью, которая больше топологической
Может быть построена рекурсивными процедурами
Слайд 6В живой природе:
Кораллы
Морские звезды и ежи
Морские раковины
Цветы и растения (брокколи, капуста)
Кроны деревьев и листья
растений
Плоды (ананас)
Кровеносная система и бронхи людей и животных
В неживой природе:
Границы географических объектов(стран, областей,
городов)Береговые линии
Снежинки
Облака
Молнии
Морозные узоры на оконных стёклах
Кристаллы
Слайд 8Обзор пакета fractals
треугольник Серпинского, фракталы «Дерево», «Папоротник»
множество Мандельброта
и множества Жюлиа
снежинки Коха
отображения Пеано: кривые Серпинского и Гильберта
Слайд 14Обзор пакета dynamics
паутинная диаграмма
бифуркационная диаграмма
эволюция орбиты одно- и двумерного отображений
«игра
в хаос»
система итерированных функций, заданная аффинными преобразованиями
множества Жюлиа, Мандельброта
