Слайд 2Введение
Разветвления трубочек трахей, листья на деревьях, вены в
руке, река, бурлящая и изгибающаяся, рынок ценных бумаг - это
все фракталы. От представителей древних цивилизаций до Майкла Джексона, ученые, математики и артисты, как и все остальные обитатели этой планеты, были зачарованы фракталами и применяли их в своей работе.
Программисты и специалисты в области компьютерной техники так же без ума от фракталов, так как фракталы бесконечной сложности и красоты могут быть сгенерированы простыми формулами на простых домашних компьютерах. Открытие фракталов было открытием новой эстетики искусства, науки и математики, а так же революцией в человеческом восприятии мира.
Цель моей работы показать красоту фрактальной графики и увидеть при изучении не только треугольники, пирамиды, углы и системы счисления, но и разнообразные фракталы.
Слайд 3Понятие "фрактал"
Понятия фрактал и фрактальная геометрия, появившиеся в
конце 70-х, с середины 80-х прочно вошли в обиход математиков
и программистов.
Фрактал (от лат. – дробленый, состоящий из фрагментов) – термин, обозначающий геометрическую фигуру, составленную из нескольких частей, каждая их которых подобна всей фигуре целиком. Небольшая часть фрактала содержит информацию о всем фрактале.
Слово «фрактал» было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта «The Fractal Geometry of Nature».
Слайд 4Роль фракталов
Роль фракталов в компьютерной графике сегодня достаточно
велика. Они приходят на помощь, например, когда требуется, с помощью
нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения компьютерной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.
Слайд 5Свойства
Одним из основных свойств фракталов является самоподобие. В
самом простом случае небольшая часть фрактала содержит информацию о всем
фрактале.
Фракталы – геометрические объекты с дробной размерностью. К примеру, размерность линии – 1, площади – 2, объема – 3. У фрактала же значение размерности может быть между 1 и 2 или между 2 и 3. К примеру, фрактальная размерность скомканного бумажного шарика приблизительно равна 2,5. В математике существует специальная сложная формула для вычисления размерности фракталов.
Слайд 6Применение фракталов
Фракталы находят все большее и большее применение
в науке. Основная причина этого заключается в том, что они
описывают реальный мир иногда даже лучше, чем традиционная физика или математика.
Слайд 7Компьютерные системы.
Наиболее полезным использованием фракталов в
компьютерной науке является фрактальное сжатие данных. В основе этого вида
сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами.
Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.
Вот несколько примеров:
Слайд 8Механика жидкостей.
Изучение турбулентности в потоках очень хорошо подстраивается
под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно
смоделировать. И здесь помогает переход к фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков
Например, атмосфера Юпитера представляет собой одно из самых захватывающих зрелищ в Солнечной системе (рис.). Между ледяным холодом космического пространства и тысячеградусной жарой в глубинах атмосферного океана гигантской планеты зарождаются циклопические облачные вихри самых причудливых форм.
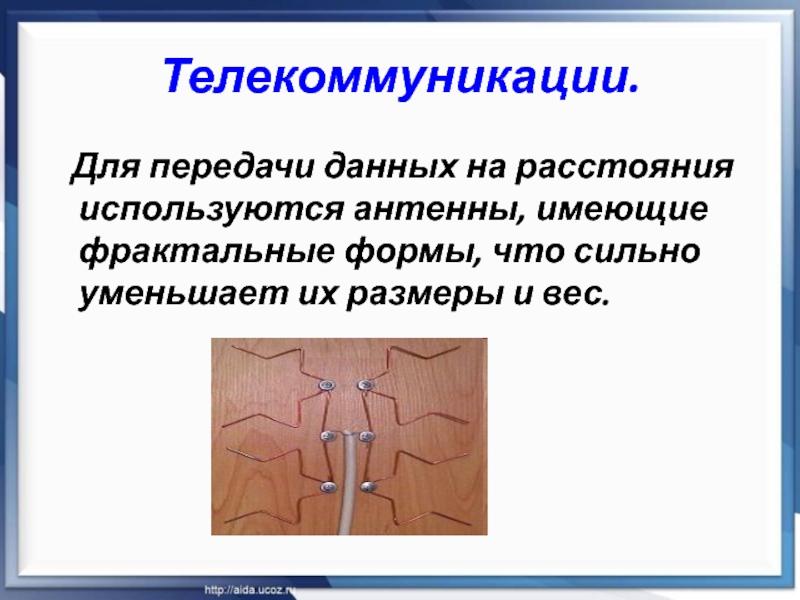
Слайд 9Телекоммуникации.
Для передачи данных на расстояния используются антенны, имеющие
фрактальные формы, что сильно уменьшает их размеры и вес.
Слайд 10Физика поверхностей.
Фракталы используются для описания кривизны поверхностей. Неровная
поверхность характеризуется комбинацией из двух разных фракталов.
Слайд 11Медицина.
Биосенсорные взаимодействия
Биения сердца
Слайд 12Биология
Моделирование хаотических процессов, в частности при описании моделей
популяций
В природе фрактальными свойствами обладают многие объекты,
например: кроны деревьев, цветная капуста, облака, кровеносная и альвеолярная системы человека и животных, кристаллы, снежинки, элементы которых выстраиваются в одну сложную структуру, побережья
Слайд 13Фрактальное искусство
Еще одной захватывающей, но спорной областью
применения фракталов служит компьютерное искусство. Фракталы не только служат ученым,
но и помогают художникам передавать их мысли, чувства и настроения, воплощая самые невероятные фантазии. В наше время живописец уже не может обойтись без компьютерной программы, которая строит причудливые картины-фракталы
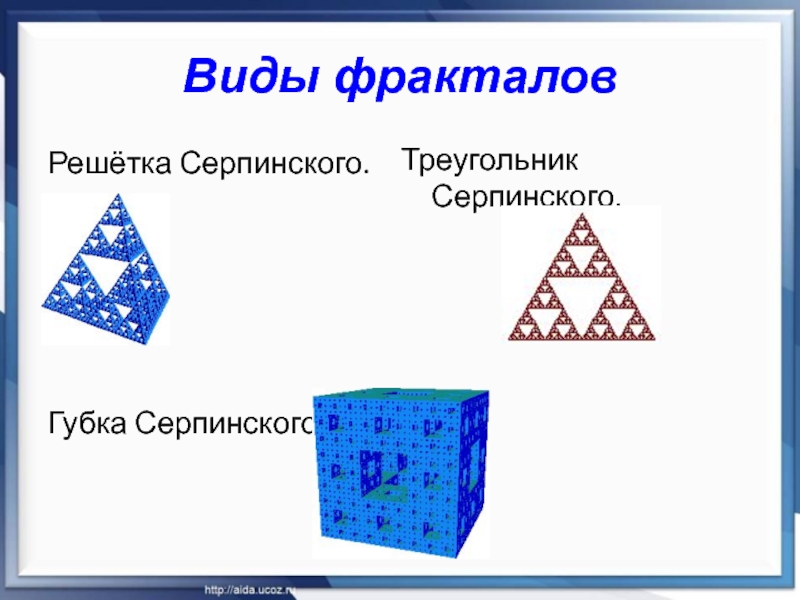
Слайд 14Виды фракталов
Решётка Серпинского.
Губка Серпинского
Треугольник
Серпинского.
Слайд 15Тетрикс (tetrix) – трехмерный аналог треугольника Серпинского
Слайд 16Кривая Коха.
Она была изобретена в девятнадцатом веке немецким математиком по
имени
Хельге фон Кох.
Инициатор - прямая линия.
Генератор – равносторонний треугольник, стороны которого равны трети длины большего отрезка. Эти треугольники добавляются к середине каждого сегмента снова и снова
Слайд 17Фрактал Мандельброта.
Это вариант кривой Коха несмотря на то, что этот
объект не похож на нее.
Вместо того, чтобы
присоединять
равносторонние треугольники к
отрезку кривой, квадраты
присоединяются к квадрату.
Слайд 18Кривая Дракона.
Изобретенная итальянским математиком Джузеппе Пеано, Кривая Дракона
или Взмах Дракона
Слайд 19Множество Мандельброта.
Множество Мандельброта, которое было построено
Бенуа Мандельбротом, наверное первая ассоциация, возникающая у людей, когда они
слышат слово фрактал.
Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями
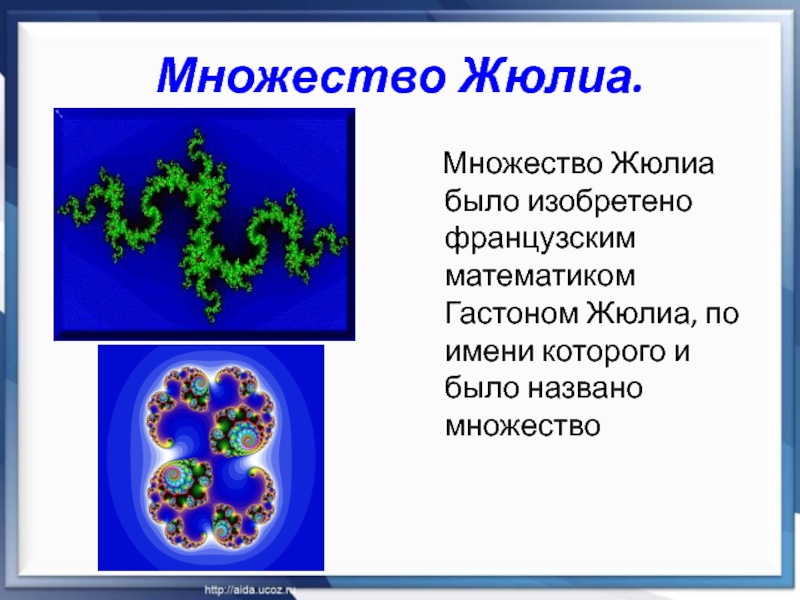
Слайд 20Множество Жюлиа.
Множество Жюлиа было изобретено французским математиком Гастоном
Жюлиа, по имени которого и было названо множество
Слайд 21Еще некоторые примеры конструктивных фракталов
Слайд 22Как построить фрактал?
Среди фрактальных графических редакторов и прочих графических
программ можно выделить:
«Art Dabbler»
«Painter» (без компьютера ни один художник
никогда не достигнет заложенных программистами возможностей лишь посредством с помощью карандаша и пера кисти)
«Adobe Photoshop» (но здесь изображение «с нуля» не создается, а, как правило, только обрабатывается)
Создатель фракталов выполняет роль художника, фотографа, скульптора, и ученого-изобретателя одновременно.
Какие предстоят этапы работы сотворения рисунка «с нуля»?
задать форму рисунка математической формулой
исследовать сходимость процесса и варьировать его параметры
выбрать вид изображения
выбрать палитру цветов
Слайд 23Заключение
Фрактальная графика - это не просто
множество самоповторяющихся изображений, это модель структуры и принципа любого сущего.
Вся наша жизнь представлена фракталами. Не только визуальными, но ещё и структура этого изображения отражает нашу жизнь. Взять, к примеру, ДНК, это всего лишь основа, одна итерация, а при повторении… появляется человек! И таких примеров много. Нельзя не отметить широкое применение фракталов в компьютерных играх, где рельефы местности зачастую являются фрактальными изображениями на основе трёхмерных моделей комплексных множеств и броуновского движения. Фрактальная графика необходима везде, и развитие "фрактальных технологий" - это одна из немаловажных задач на сегодняшний день.