ГРАФЫ. ПОИСК ПУТЕЙ В ГРАФЕ

Содержание

1. ГРАФЫ. ПОИСК ПУТЕЙ В ГРАФЕ
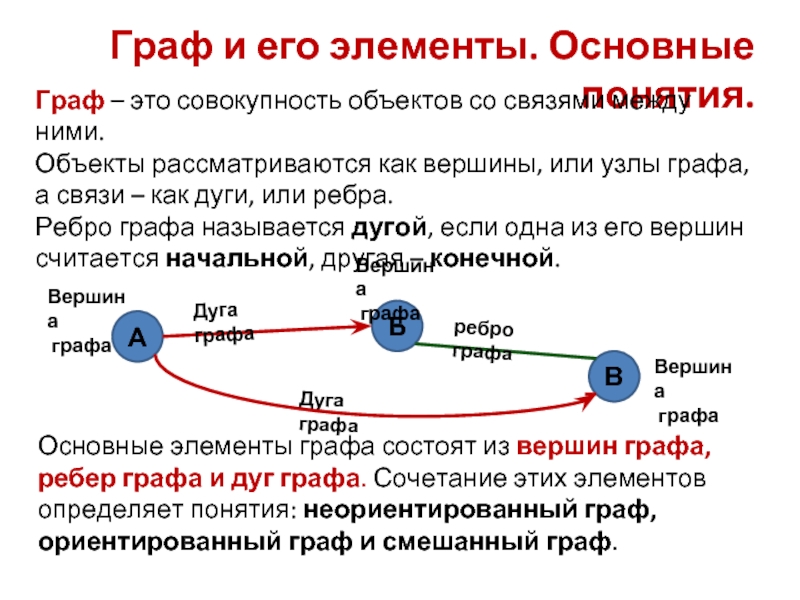
2. Граф и его элементы. Основные понятия. Граф – это
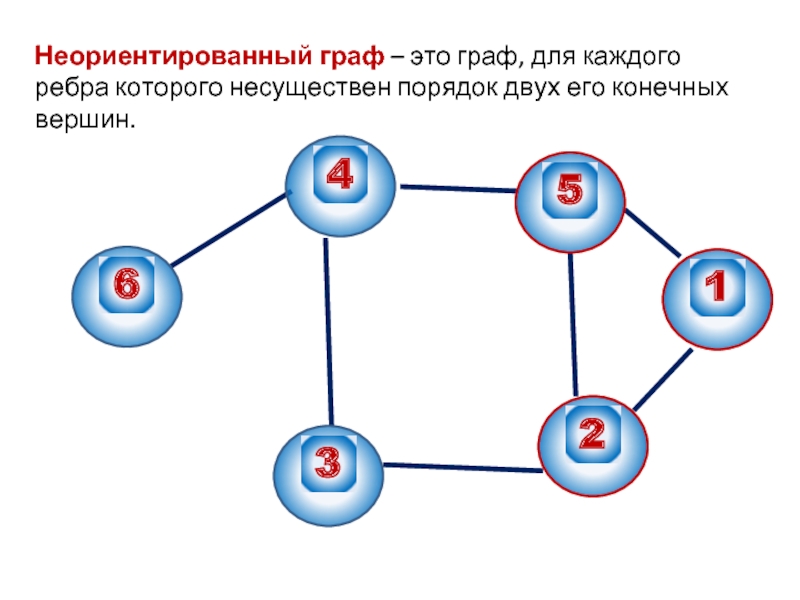
3. Неориентированный граф – это граф, для каждого ребра которого несуществен порядок двух его конечных вершин.
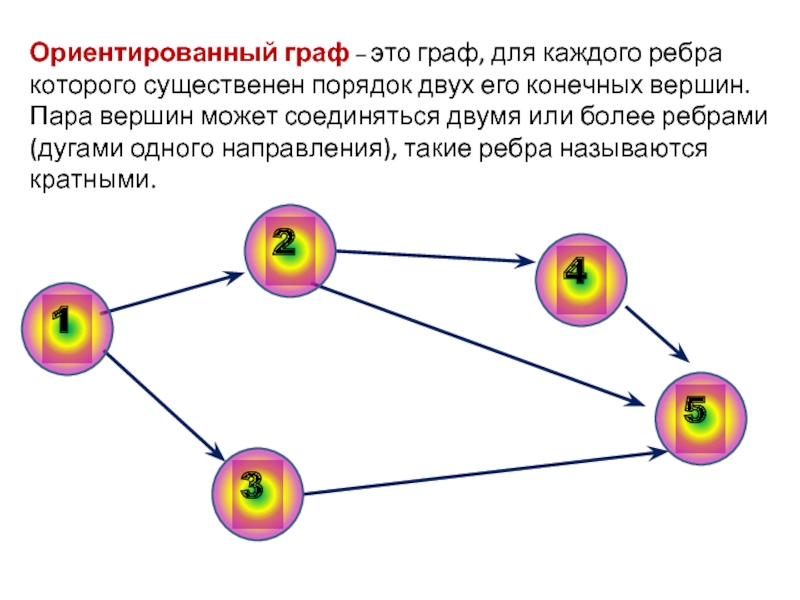
4. Ориентированный граф – это граф, для каждого ребра которого
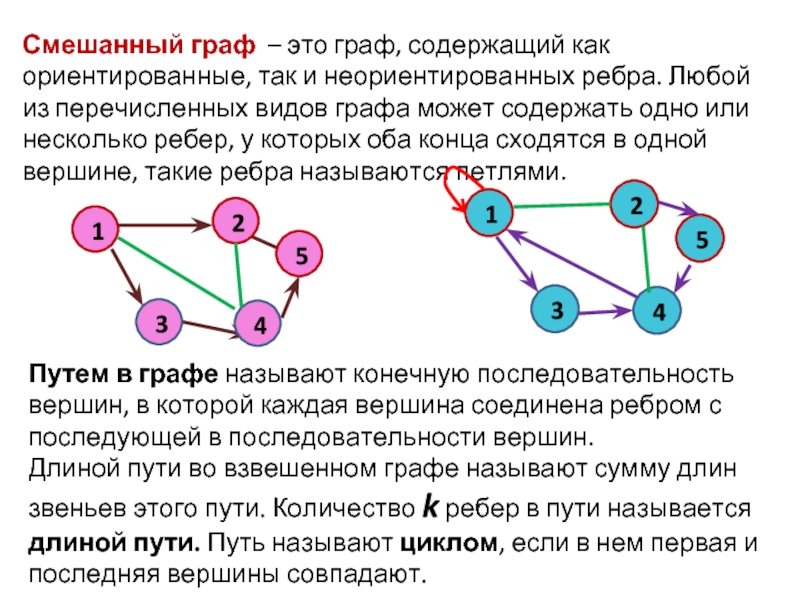
5. Смешанный граф – это граф, содержащий как ориентированные,
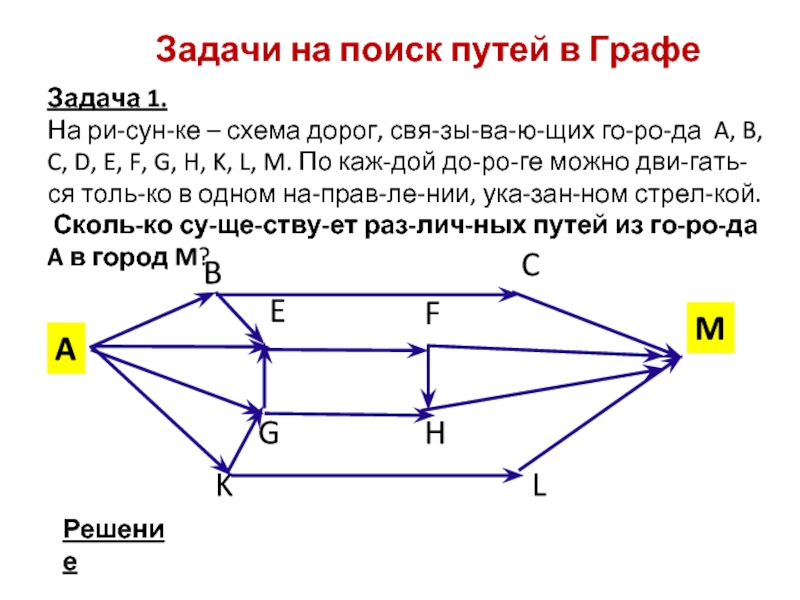
6. 12Задачи на поиск путей в ГрафеЗадача 1.На
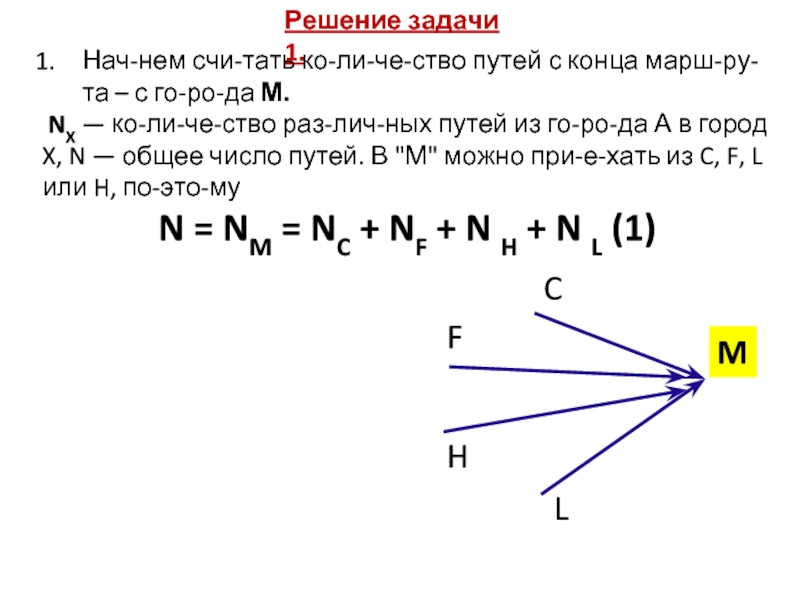
7. Решение задачи 1.Начнем считать количество путей с
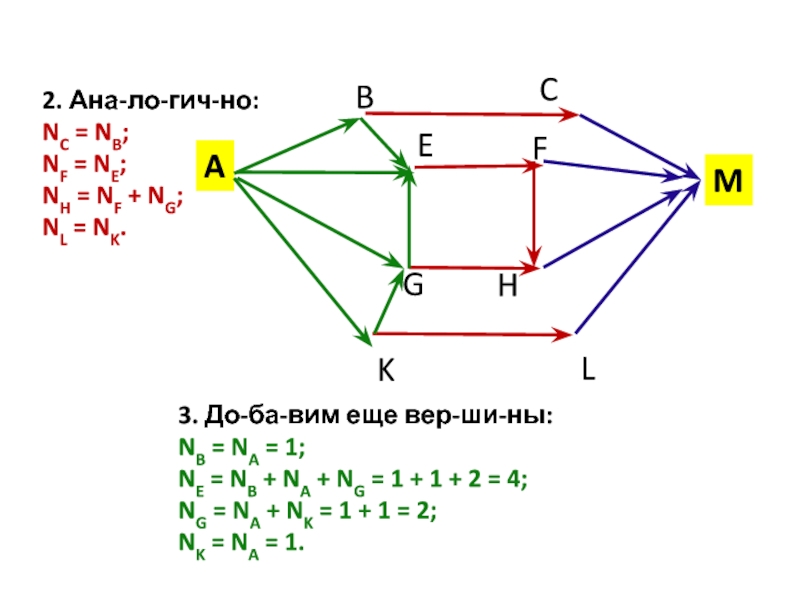
8. 2. Аналогично:NC = NB;NF = NE;NH = NF + NG;NL = NK.CFHLMBEGKA3.
9. 4. Преобразуем вершины:NC = NB = 1;NF = NE = 4;NH =
10. Задача 2.На рисунке – схема дорог, связывающих
11. Решение задачи 2.1. Начнем считать количество путей
12. 2. Аналогично: NД = NБ;
13. 4. Преобразуем первые вершины с учето значений
14. Задача 3.На рисунке изображена схема дорог, связывающих
15. Решение задачи 3.1. Начнем считать количество путей
16. Решите самостоятельно:1). На рисунке — схема дорог,
17. 2).На рисунке — схема дорог, связывающих города
18. 3).На рисунке изображена схема дорог, связывающих города
19. Задание на дом:На рисунке изображена схема дорог,
20. Источники информации:http://www.compress.ru/Archive/CP/2007/1/18/10.gifhttp://kpolyakov.narod.ru/school/ege.htmhttp://inf.reshuege.ru/test?theme=203http://inf.reshuege.ru/get_file?id=3029
21. Скачать презентанцию

Граф и его элементы. Основные понятия. Граф – это совокупность объектов со связями между ними. Объекты рассматриваются как вершины, или узлы графа, а связи – как дуги, или ребра.Ребро графа называется дугой, если одна из его

Слайды и текст этой презентации

Слайд 1ГРАФЫ.
ПОИСК ПУТЕЙ В ГРАФЕ.
Автор: Сергеенкова И.М.,
ГБОУ Школа № 1191,

г. Москва

Слайд 2Граф и его элементы. Основные понятия.
Граф – это совокупность объектов со

связями между ними.
Объекты рассматриваются как вершины, или узлы графа,
а

связи – как дуги, или ребра.
Ребро графа называется дугой, если одна из его вершин считается начальной, другая – конечной.

Основные элементы графа состоят из вершин графа, ребер графа и дуг графа. Сочетание этих элементов определяет понятия: неориентированный граф, ориентированный граф и смешанный граф.

Дуга графа

ребро графа

Вершина
графа

Граф и его элементы. Основные понятия. Граф – это совокупность объектов со связями между ними. Объекты рассматриваются как вершины, или

Слайд 3Неориентированный граф – это граф, для каждого ребра которого несуществен порядок двух

его конечных вершин.

Слайд 4Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух

его конечных вершин.
Пара вершин может соединяться двумя или более ребрами

(дугами одного направления), такие ребра называются кратными.

Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух его конечных вершин.Пара вершин может соединяться двумя

Слайд 5Смешанный граф – это граф, содержащий как ориентированные, так и неориентированных

ребра. Любой из перечисленных видов графа может содержать одно или несколько

ребер, у которых оба конца сходятся в одной вершине, такие ребра называются петлями.

Путем в графе называют конечную последовательность вершин, в которой каждая вершина соединена ребром с последующей в последовательности вершин.
Длиной пути во взвешенном графе называют сумму длин звеньев этого пути. Количество k ребер в пути называется длиной пути. Путь называют циклом, если в нем первая и последняя вершины совпадают.

Смешанный граф – это граф, содержащий как ориентированные, так и неориентированных ребра. Любой из перечисленных видов графа может содержать

Слайд 612
Задачи на поиск путей в Графе
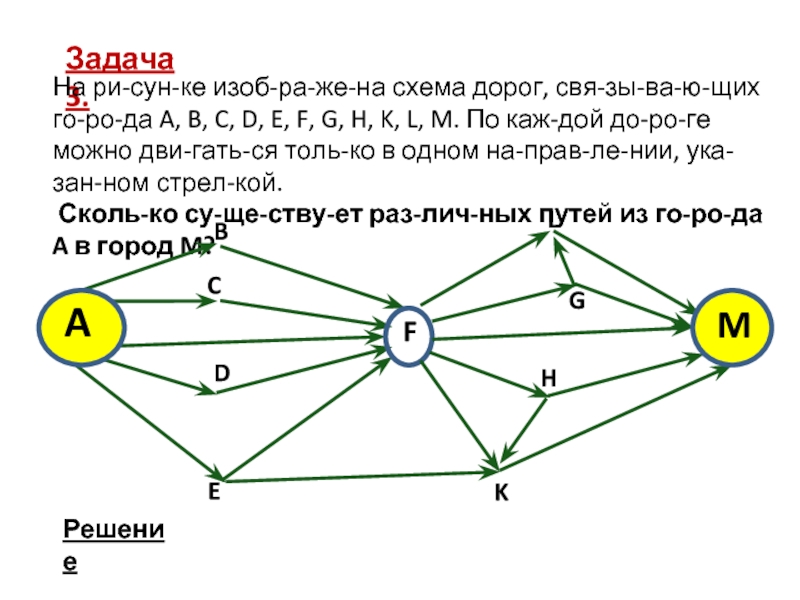
Задача 1.
На рисунке – схема

дорог, связывающих города A, B, C, D, E, F, G,

H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города A в город M?

Решение

12Задачи на поиск путей в ГрафеЗадача 1.На рисунке – схема дорог, связывающих города A, B, C, D,

Слайд 7Решение задачи 1.
Начнем считать количество путей с конца маршрута –

с города М.
NX — количество различных путей из города А

в город X, N — общее число путей. В "М" можно приехать из C, F, L или H, поэтому
N = NM = NC + NF + N H + N L (1)

Решение задачи 1.Начнем считать количество путей с конца маршрута – с города М. NX — количество различных путей

Слайд 82. Аналогично:
NC = NB;
NF = NE;
NH = NF + NG;
NL = NK.
C
F
H
L
M
B
E
G
K
A
3. Добавим еще вершины:
NB =

NA = 1;
NE = NB + NA + NG = 1 + 1 + 2

= 4;
NG = NA + NK = 1 + 1 = 2;
NK = NA = 1.

2. Аналогично:NC = NB;NF = NE;NH = NF + NG;NL = NK.CFHLMBEGKA3. Добавим еще вершины:NB = NA = 1;NE = NB + NA + NG = 1 +

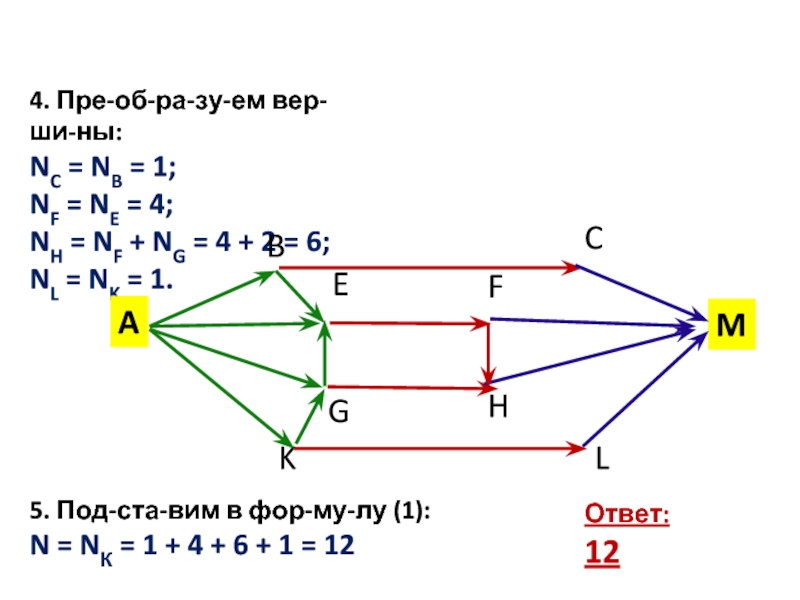
Слайд 94. Преобразуем вершины:
NC = NB = 1;
NF = NE = 4;
NH = NF + NG = 4

+ 2 = 6;
NL = NK = 1.
5. Подставим в формулу (1):
N

= NК = 1 + 4 + 6 + 1 = 12

Ответ: 12

4. Преобразуем вершины:NC = NB = 1;NF = NE = 4;NH = NF + NG = 4 + 2 = 6;NL = NK = 1.5. Подставим

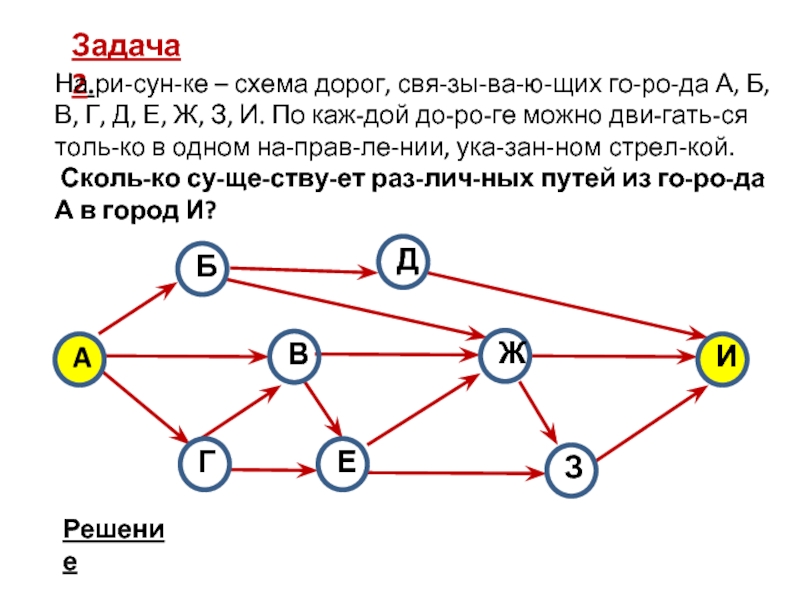
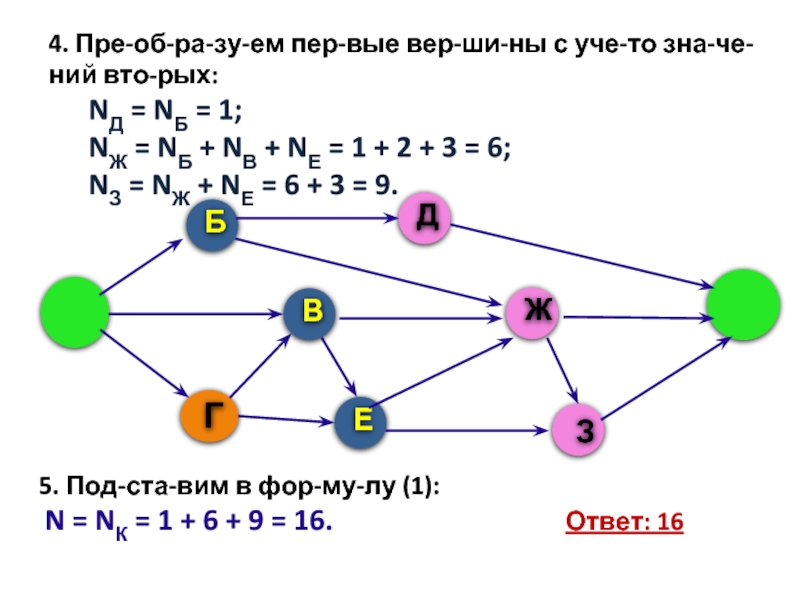
Слайд 10Задача 2.
На рисунке – схема дорог, связывающих города А, Б,

В, Г, Д, Е, Ж, З, И. По каждой дороге

можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город И?

Решение

Задача 2.На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И.

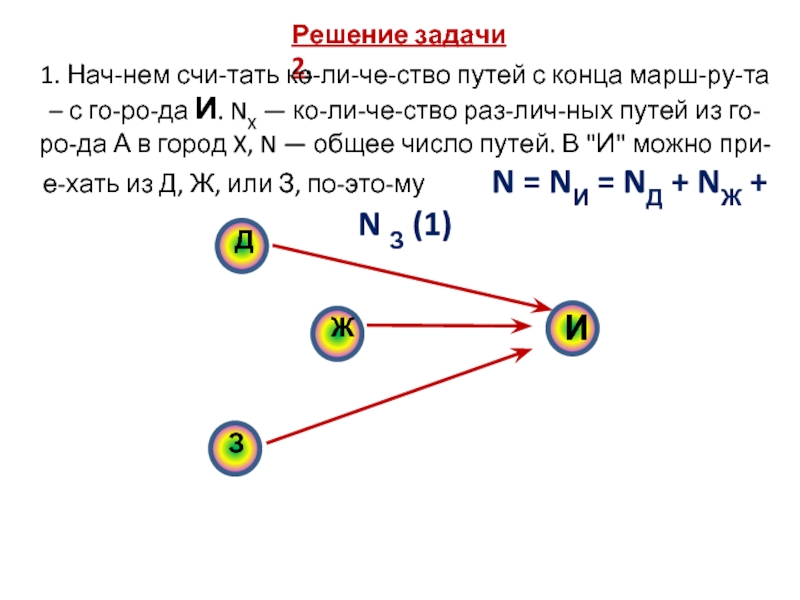
Слайд 11Решение задачи 2.
1. Начнем считать количество путей с конца маршрута

– с города И. NX — количество различных путей из города

А в город X, N — общее число путей. В "И" можно приехать из Д, Ж, или З, поэтому N = NИ = NД + NЖ + N З (1)

Решение задачи 2.1. Начнем считать количество путей с конца маршрута – с города И. NX — количество различных

Слайд 122. Аналогично:
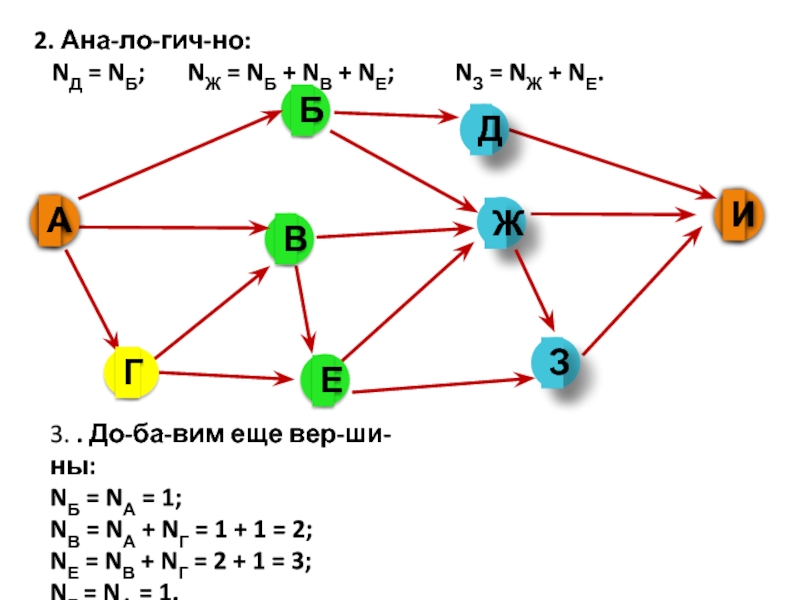
NД = NБ; NЖ = NБ +

NВ + NЕ; NЗ = NЖ + NЕ.
3. .

Добавим еще вершины:
NБ = NА = 1;
NВ = NА + NГ = 1 + 1 = 2;
NЕ = NВ + NГ = 2 + 1 = 3;
NГ = NА = 1.

2. Аналогично: NД = NБ; NЖ = NБ + NВ + NЕ; NЗ =

Слайд 134. Преобразуем первые вершины с учето значений вторых:
NД = NБ = 1;
NЖ =

NБ + NВ + NЕ = 1 + 2 + 3 = 6;
NЗ =

NЖ + NЕ = 6 + 3 = 9.

5. Подставим в формулу (1):
N = NК = 1 + 6 + 9 = 16. Ответ: 16

4. Преобразуем первые вершины с учето значений вторых: NД = NБ = 1; NЖ = NБ + NВ + NЕ = 1 + 2 +

Слайд 14Задача 3.
На рисунке изображена схема дорог, связывающих города A, B,

C, D, E, F, G, H, K, L, M. По

каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города A в город M?

Решение

Задача 3.На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F, G, H, K,

Слайд 15Решение задачи 3.
1. Начнем считать количество путей с конца маршрута

— с города M. Пусть NX — количество различных путей из

города А в город X, N — общее число путей. В город M можно приехать из L, G, F, H или K, поэтому N = NM = NL + NG+NF+ NH + NK;(*)

2.Аналогично:
NL = NF+ NG = 5 + 5 = 10;
NG = NF = 5;
NH = NF = 5;
NK = NF + NE + NH = 5 + 1 + 5 = 11;
NF = NA + NB + NC + ND + NE = = 5.

3. Добавим еще вершины:
NB = NA = 1;
NC = NA = 1;
ND = NA = 1;
NE = NA = 1.

4. Подставим в формулу :
N = NM = 10 + 5 + 5 + 11 + 5 = 36.

Ответ: 36.

Решение задачи 3.1. Начнем считать количество путей с конца маршрута — с города M. Пусть NX — количество

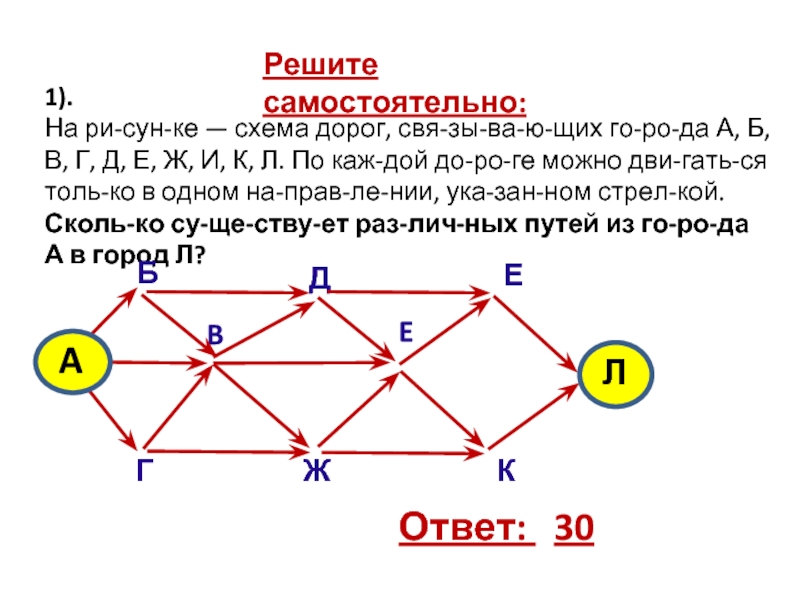
Слайд 16Решите самостоятельно:
1).
На рисунке — схема дорог, связывающих города А,

Б, В, Г, Д, Е, Ж, И, К, Л. По

каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Л?

Ответ: 30

Решите самостоятельно:1). На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И,

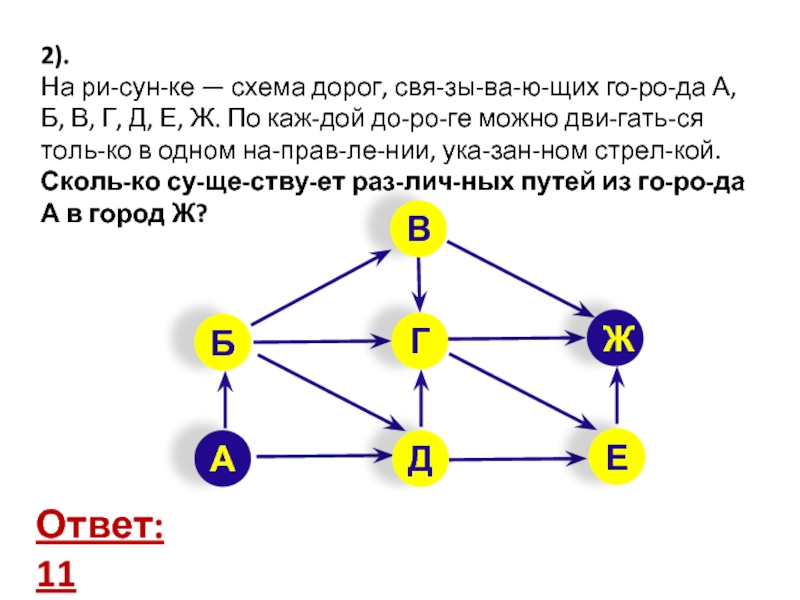
Слайд 172).
На рисунке — схема дорог, связывающих города А, Б, В,

Г, Д, Е, Ж. По каждой дороге можно двигаться только

в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Ж?

Ответ: 11

2).На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге

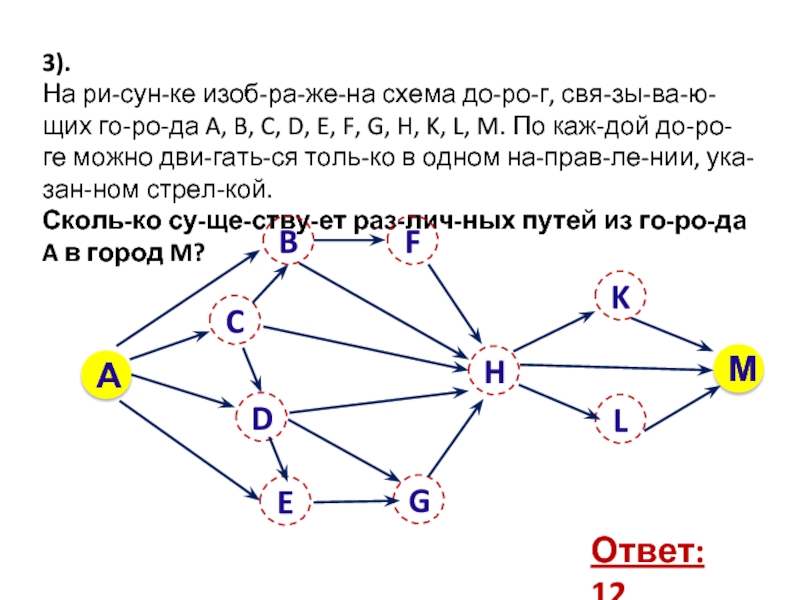
Слайд 183).
На рисунке изображена схема дорог, связывающих города A, B, C,

D, E, F, G, H, K, L, M. По каждой

дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города A в город M?

Ответ: 12

3).На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L,

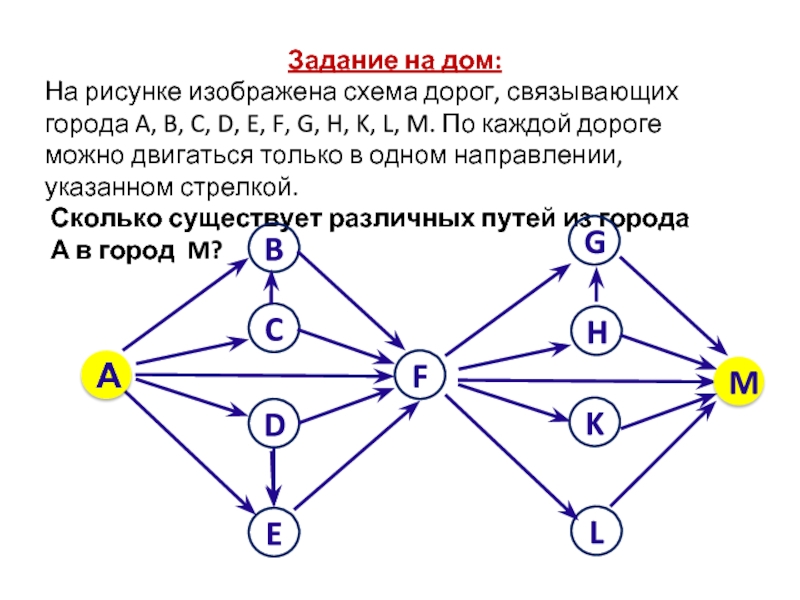
Слайд 19Задание на дом:
На рисунке изображена схема дорог, связывающих города A,

B, C, D, E, F, G, H, K, L, M.

По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города
А в город M?

Задание на дом:На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F, G, H,

Слайд 20Источники информации:

http://www.compress.ru/Archive/CP/2007/1/18/10.gif
http://kpolyakov.narod.ru/school/ege.htm
http://inf.reshuege.ru/test?theme=203
http://inf.reshuege.ru/get_file?id=3029

Источники информации:http://www.compress.ru/Archive/CP/2007/1/18/10.gifhttp://kpolyakov.narod.ru/school/ege.htmhttp://inf.reshuege.ru/test?theme=203http://inf.reshuege.ru/get_file?id=3029

Скачать презентацию

Разделы презентаций

ГРАФЫ. ПОИСК ПУТЕЙ В ГРАФЕ

Содержание

Слайды и текст этой презентации

Слайд 1ГРАФЫ.ПОИСК ПУТЕЙ В ГРАФЕ.Автор: Сергеенкова И.М., ГБОУ Школа № 1191,

г. Москва

Слайд 2Граф и его элементы. Основные понятия. Граф – это совокупность объектов со

связями между ними. Объекты рассматриваются как вершины, или узлы графа, а

Слайд 3Неориентированный граф – это граф, для каждого ребра которого несуществен порядок двух

его конечных вершин.

Слайд 4Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух

его конечных вершин.Пара вершин может соединяться двумя или более ребрами

Слайд 5Смешанный граф – это граф, содержащий как ориентированные, так и неориентированных

ребра. Любой из перечисленных видов графа может содержать одно или несколько

Слайд 612Задачи на поиск путей в ГрафеЗадача 1.На ри­сун­ке – схема

дорог, свя­зы­ва­ю­щих го­ро­да A, B, C, D, E, F, G,

Слайд 7Решение задачи 1.Нач­нем счи­тать ко­ли­че­ство путей с конца марш­ру­та –

с го­ро­да М. NX — ко­ли­че­ство раз­лич­ных путей из го­ро­да А

Слайд 82. Ана­ло­гич­но:NC = NB;NF = NE;NH = NF + NG;NL = NK.CFHLMBEGKA3. До­ба­вим еще вер­ши­ны:NB =

NA = 1;NE = NB + NA + NG = 1 + 1 + 2

Слайд 94. Пре­об­ра­зу­ем вер­ши­ны:NC = NB = 1;NF = NE = 4;NH = NF + NG = 4

+ 2 = 6;NL = NK = 1.5. Под­ста­вим в фор­му­лу (1):N

Слайд 10Задача 2.На ри­сун­ке – схема дорог, свя­зы­ва­ю­щих го­ро­да А, Б,

В, Г, Д, Е, Ж, З, И. По каж­дой до­ро­ге

Слайд 11Решение задачи 2.1. Нач­нем счи­тать ко­ли­че­ство путей с конца марш­ру­та

– с го­ро­да И. NX — ко­ли­че­ство раз­лич­ных путей из го­ро­да

Слайд 122. Ана­ло­гич­но: NД = NБ; NЖ = NБ +

NВ + NЕ; NЗ = NЖ + NЕ.3. .

Слайд 134. Пре­об­ра­зу­ем пер­вые вер­ши­ны с уче­то зна­че­ний вто­рых: NД = NБ = 1; NЖ =

NБ + NВ + NЕ = 1 + 2 + 3 = 6; NЗ =

Слайд 14Задача 3.На ри­сун­ке изоб­ра­же­на схема дорог, свя­зы­ва­ю­щих го­ро­да A, B,

C, D, E, F, G, H, K, L, M. По

Слайд 15Решение задачи 3.1. Нач­нем счи­тать ко­ли­че­ство путей с конца марш­ру­та

— с го­ро­да M. Пусть NX — ко­ли­че­ство раз­лич­ных путей из

Слайд 16Решите самостоятельно:1). На ри­сун­ке — схема дорог, свя­зы­ва­ю­щих го­ро­да А,

Б, В, Г, Д, Е, Ж, И, К, Л. По

Слайд 172).На ри­сун­ке — схема дорог, свя­зы­ва­ю­щих го­ро­да А, Б, В,

Г, Д, Е, Ж. По каж­дой до­ро­ге можно дви­гать­ся толь­ко

Слайд 183).На ри­сун­ке изоб­ра­же­на схема до­ро­г, свя­зы­ва­ю­щих го­ро­да A, B, C,

D, E, F, G, H, K, L, M. По каж­дой

Слайд 19Задание на дом:На рисунке изображена схема дорог, связывающих города A,

B, C, D, E, F, G, H, K, L, M.

Слайд 20Источники информации:http://www.compress.ru/Archive/CP/2007/1/18/10.gifhttp://kpolyakov.narod.ru/school/ege.htmhttp://inf.reshuege.ru/test?theme=203http://inf.reshuege.ru/get_file?id=3029

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1ГРАФЫ.
ПОИСК ПУТЕЙ В ГРАФЕ.
Автор: Сергеенкова И.М.,
ГБОУ Школа № 1191,

Слайд 2Граф и его элементы. Основные понятия.
Граф – это совокупность объектов со

связями между ними.
Объекты рассматриваются как вершины, или узлы графа,
а

его конечных вершин.
Пара вершин может соединяться двумя или более ребрами

Слайд 612
Задачи на поиск путей в Графе
Задача 1.
На рисунке – схема

дорог, связывающих города A, B, C, D, E, F, G,

Слайд 7Решение задачи 1.
Начнем считать количество путей с конца маршрута –

с города М.
NX — количество различных путей из города А

Слайд 82. Аналогично:
NC = NB;
NF = NE;
NH = NF + NG;
NL = NK.
C
F
H
L
M
B
E
G
K
A
3. Добавим еще вершины:
NB =

NA = 1;
NE = NB + NA + NG = 1 + 1 + 2

Слайд 94. Преобразуем вершины:
NC = NB = 1;
NF = NE = 4;
NH = NF + NG = 4

+ 2 = 6;
NL = NK = 1.
5. Подставим в формулу (1):
N

Слайд 10Задача 2.
На рисунке – схема дорог, связывающих города А, Б,

В, Г, Д, Е, Ж, З, И. По каждой дороге

Слайд 11Решение задачи 2.
1. Начнем считать количество путей с конца маршрута

– с города И. NX — количество различных путей из города

Слайд 122. Аналогично:
NД = NБ; NЖ = NБ +

NВ + NЕ; NЗ = NЖ + NЕ.
3. .

Слайд 134. Преобразуем первые вершины с учето значений вторых:
NД = NБ = 1;
NЖ =

NБ + NВ + NЕ = 1 + 2 + 3 = 6;
NЗ =

Слайд 14Задача 3.
На рисунке изображена схема дорог, связывающих города A, B,

Слайд 15Решение задачи 3.
1. Начнем считать количество путей с конца маршрута

— с города M. Пусть NX — количество различных путей из

Слайд 16Решите самостоятельно:
1).
На рисунке — схема дорог, связывающих города А,

Слайд 172).
На рисунке — схема дорог, связывающих города А, Б, В,

Г, Д, Е, Ж. По каждой дороге можно двигаться только

Слайд 183).
На рисунке изображена схема дорог, связывающих города A, B, C,

D, E, F, G, H, K, L, M. По каждой

Слайд 19Задание на дом:
На рисунке изображена схема дорог, связывающих города A,

Слайд 20Источники информации:

http://www.compress.ru/Archive/CP/2007/1/18/10.gif
http://kpolyakov.narod.ru/school/ege.htm
http://inf.reshuege.ru/test?theme=203
http://inf.reshuege.ru/get_file?id=3029