Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исполнители в ЕГЭ
Содержание
- 1. Исполнители в ЕГЭ
- 2. Уметь размышлять и анализироватьУметь выполнять алгоритмы в среде формального Исполнителя алгоритмовНеобходимые знания и умения
- 3. 2004-2005 год (А)2006 год (А)2008 год (А)2009
- 4. ЕГЭ 2004-2005 (А)Исполнитель Черепашка перемещается на экране
- 5. Повтори 4 (Вперед 10 Направо 120)1 способ:Черепашка
- 6. Повтори 4 (Вперед 10 Направо 120)1 способ:360:120=3(правильный
- 7. Повтори 4 (Вперед 10 Направо 120)1 способ:360:120=3(правильный
- 8. Повтори 4 (Вперед 10 Направо 120)1 способ:360:120=3(правильный
- 9. ЕГЭ-2006 (А)Какое число необходимо записать вместо n
- 10. ЕГЭ – 2008 (А)
- 11. Решение:А : = “поезд”5 >0
- 12. Решение:А : = “поезд”3 >0
- 13. Решение:А : = “поезд”1 >0
- 14. Решение:А : = “поезд”-1 >0Ответ: АДЕПТ
- 15. ЕГЭ -2009 (А)
- 16. Решение:пока справа свободно -вправопока сверху свободно –вверхпока слева свободно –влевопока снизу свободно -вниз
- 17. Решение:пока справа свободно -вправопока сверху свободно –вверхпока слева свободно –влевопока снизу свободно -внизОтвет : 4
- 18. ЕГЭ -2010 (А)
- 19. Решение:пока сверху свободно –вправопока справа свободно –внизпока
- 20. Решение:пока сверху свободно –вправопока справа свободно –внизпока снизу свободно –влевопока слева свободно –вверхОтвет : 1
- 21. ЕГЭ - 2011
- 22. Решение:
- 23. Ответ: 3
- 24. Система команд исполнителя РОБОТ, «живущего» в прямоугольном
- 25. Решение:1. Легко понять, что для того, чтобы
- 26. 5. Этих «подозрительных» клеток не так много,
- 27. ЕГЭ – 2008 (В) Исполнитель Робот действует
- 28. Решение:1 (вверх), 2 (вниз), 3 (влево), 4 (вправо), 1132432Ответ : 1 4 2
- 29. ЕГЭ – 2009 (В)На экране есть два
- 30. Решение:
- 31. Решение:
- 32. Решение:
- 33. Решение:
- 34. Решение:
- 35. Решение:
- 36. ЕГЭ – 2011 (В)У исполнителя Калькулятор
- 37. Решение:Прибавь 3Умножь на 4.
- 38. Решение:Прибавь 3Умножь на 4.
- 39. Решение:Прибавь 3Умножь на 4.
- 40. Решение:Прибавь 3Умножь на 4.
- 41. Решение:Прибавь 3Умножь на 4.
- 42. ЕГЭ – 2012 (В)У исполнителя Кузнечик две
- 43. Решение 1. Построение полного графа решений 1.
- 44. 3. Строим еще уровень: 3 команды дают
- 45. Решение 2. Краткий способ Как следует из
- 46. Литература:Сборник экзаменационных заданий ЕГЭ 2008- 2011 (Москва,
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Исполнители в ЕГЭ
Буткевич Ирина Владиславовна, учитель информатики
МБОУСОШ №22 г.Новочеркасска
Слайд 2Уметь размышлять и анализировать
Уметь выполнять алгоритмы в среде формального Исполнителя
алгоритмов
Слайд 32004-2005 год (А)
2006 год (А)
2008 год (А)
2009 год (А)
2010 год
(А)
2011 год (А)
2012 год (А)
2008 год (В)
2009 год (В)
2011 год
(В)2012 год (В)
Задания ЕГЭ
Слайд 4ЕГЭ 2004-2005 (А)
Исполнитель Черепашка перемещается на экране компьютера, оставляя след
в виде линии. В каждый конкретный момент известно положение исполнителя
и направление его движения. У исполнителя существуют две команды:Вперед n , где n- целое число шагов в направлении движения
Направо n, где n- целое число градусов поворота по часовой стрелке.
Черепашке был дан для исполнения следующий алгоритм:
Повтори 4 (Вперед 10 Направо 120)
Какая фигура появится на экране?
Незамкнутая ломаная
Правильный треугольник
Квадрат
Правильный пятиугольник
Слайд 5Повтори 4 (Вперед 10 Направо 120)
1 способ:
Черепашка прочертит на экране
4 линии, но последний отрезок полностью совпадет с первым, т.к.
после третьего выполнения цикла Черепашка обернется вокруг своей оси (360 0)360:120=3
(правильный треугольник)
2 способ:
180-120=60 –внутренний угол
180: 60=3
(правильный треугольник)
3 способ
Построение
Вперед 10
Решение:
Слайд 6Повтори 4 (Вперед 10 Направо 120)
1 способ:
360:120=3
(правильный треугольник)
2 способ:
180-120=60 –внутренний
угол
180: 60=3
(правильный треугольник)
3 способ
Построение
Вперед 10 Направо 120
Слайд 7Повтори 4 (Вперед 10 Направо 120)
1 способ:
360:120=3
(правильный треугольник)
2 способ:
180-120=60 –внутренний
угол
180: 60=3
(правильный треугольник)
3 способ
Построение
Вперед 10 Направо 120
Вперед 10 Направо
120Слайд 8Повтори 4 (Вперед 10 Направо 120)
1 способ:
360:120=3
(правильный треугольник)
2 способ:
180-120=60 –внутренний
угол
180: 60=3
(правильный треугольник)
3 способ
Построение
Вперед 10 Направо 120
Вперед 10 Направо
120Вперед 10 Направо 120
Слайд 9ЕГЭ-2006 (А)
Какое число необходимо записать вместо n в алгоритме:
Повтори 7
(Вперед 40 Направо n)
Чтобы на экране появился правильный шестиугольник?
1) 30
2) 45 3) 50 4) 601 способ:
Сумма внутренних углов многоугольника (р-2)*180,
Величина одного внутреннего угла – (р – 2)* 180 / р
4 * 180 / 6 = 120
Смежный угол- 60
2 способ:
Черепашка прочертит на экране 7 отрезков, но последний совпадет с первым (черепашка полностью повернется вокруг своей оси на 3600)
360 : 6 =60
Ответ: 60
Слайд 16Решение:
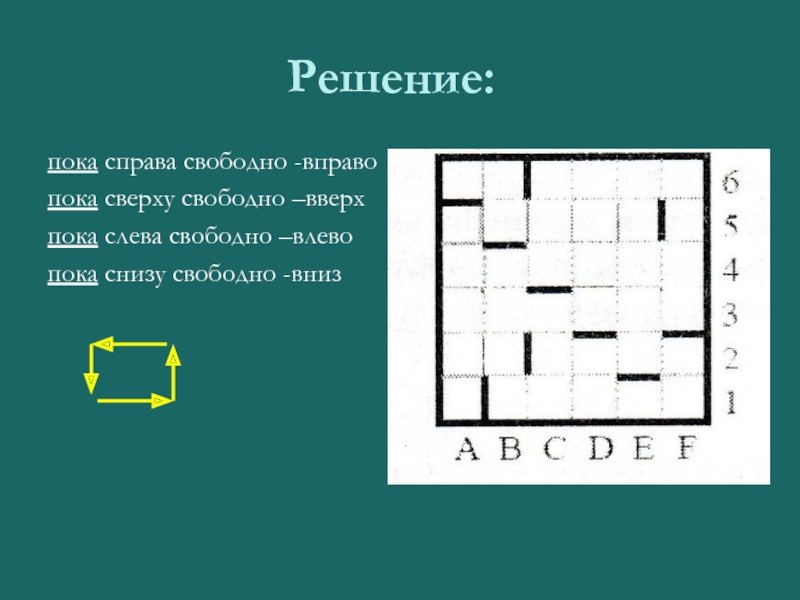
пока справа свободно -вправо
пока сверху свободно –вверх
пока слева свободно –влево
пока
снизу свободно -вниз
Слайд 17Решение:
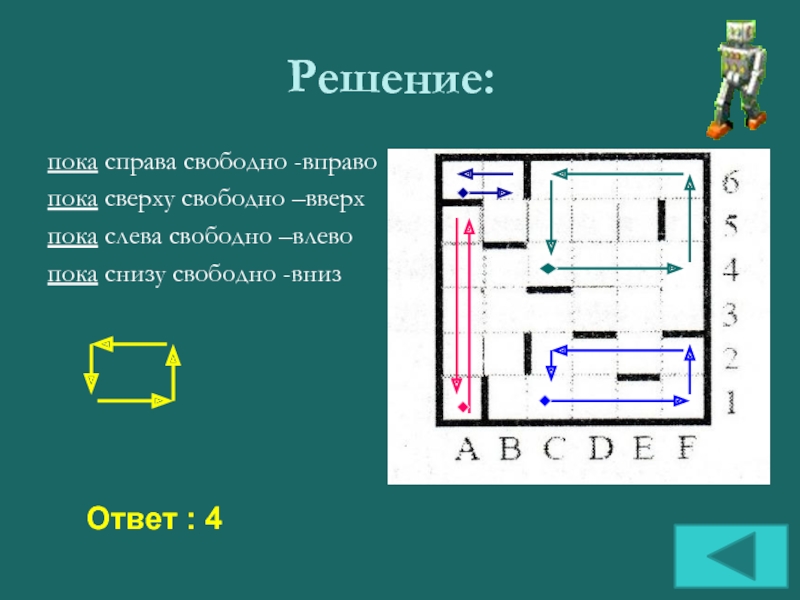
пока справа свободно -вправо
пока сверху свободно –вверх
пока слева свободно –влево
пока
снизу свободно -вниз
Ответ : 4
Слайд 19Решение:
пока сверху свободно –вправо
пока справа свободно –вниз
пока снизу свободно –влево
пока
слева свободно –вверх
Сложность задания:
Робот проверяет стену в одном направлении, а
движется в другомРобот
разрушается
Слайд 20Решение:
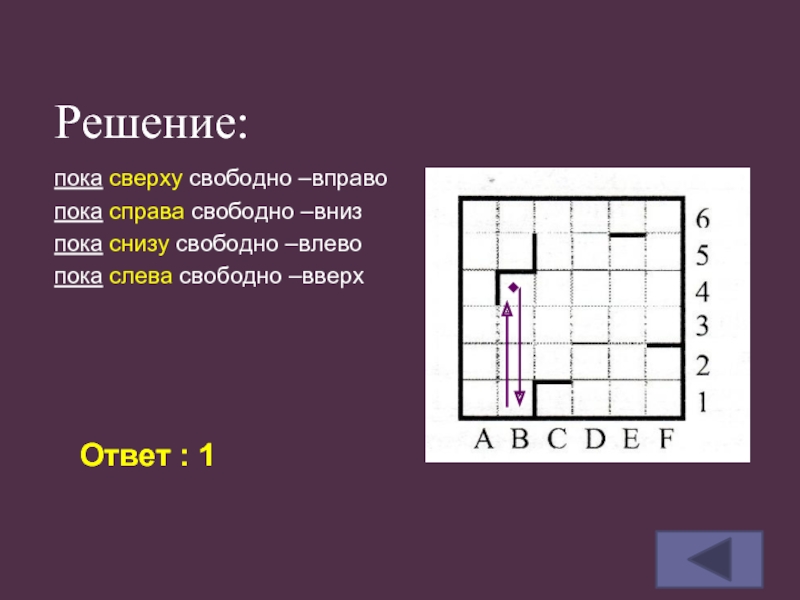
пока сверху свободно –вправо
пока справа свободно –вниз
пока снизу свободно –влево
пока
слева свободно –вверх
Ответ : 1
Слайд 24
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой
плоскости:
вверх вниз влево вправо.
При выполнении любой из
этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той
клетки, где находится РОБОТ:
сверху свободно снизу свободно
слева свободно справа свободно
Цикл ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив
предложенную ниже программу, РОБОТ уцелеет (не врежется в стену) и остановится
в той же клетке, с которой он начал движение?
1) 1 2) 2 3) 3 4) 0
НАЧАЛО
ПОКА <слева свободно> вверх
ПОКА <сверху свободно> вправо
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
КОНЕЦ
ЕГЭ – 2012 (А)
Слайд 25Решение:
1. Легко понять, что для того, чтобы исполнитель вернулся обратно
в ту клетку, откуда он начал движения, четыре
стенки должны быть расставлены так, чтобы он упирался в них сначала при движении вниз, затем – влево, вверх и, наконец, вправо:на рисунке красная точка обозначает клетку, начав с которой РОБОТ
вернется обратно;
2. Кроме этих четырех стенок, необходимо, чтобы коридор, выделенный на рисунке справа зеленым
фоном, был свободен для прохода.
3. Обратим внимание, что возможны еще «вырожденные» варианты, вроде таких:
4. Итак, мы выяснили, что нужно рассматривать лишь те клетки,
где есть стенка справа;
отметим на исходной карте клетки-кандидаты:
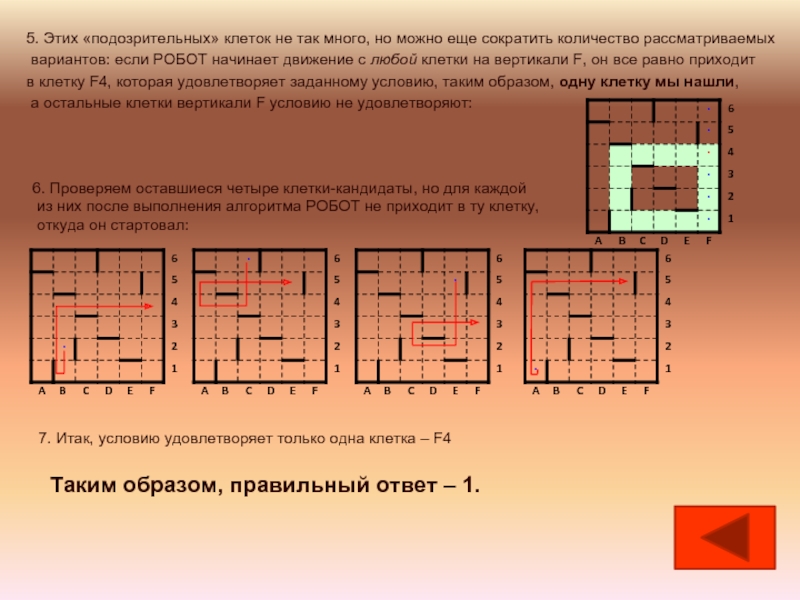
Слайд 265. Этих «подозрительных» клеток не так много, но можно еще
сократить количество рассматриваемых
вариантов: если РОБОТ начинает движение с любой
клетки на вертикали F, он все равно приходит в клетку F4, которая удовлетворяет заданному условию, таким образом, одну клетку мы нашли,
а остальные клетки вертикали F условию не удовлетворяют:
6. Проверяем оставшиеся четыре клетки-кандидаты, но для каждой
из них после выполнения алгоритма РОБОТ не приходит в ту клетку,
откуда он стартовал:
7. Итак, условию удовлетворяет только одна клетка – F4
Таким образом, правильный ответ – 1.
Слайд 27ЕГЭ – 2008 (В)
Исполнитель Робот действует на клетчатой доске,
между соседними клетками которой могут стоять стены. Робот передвигается по
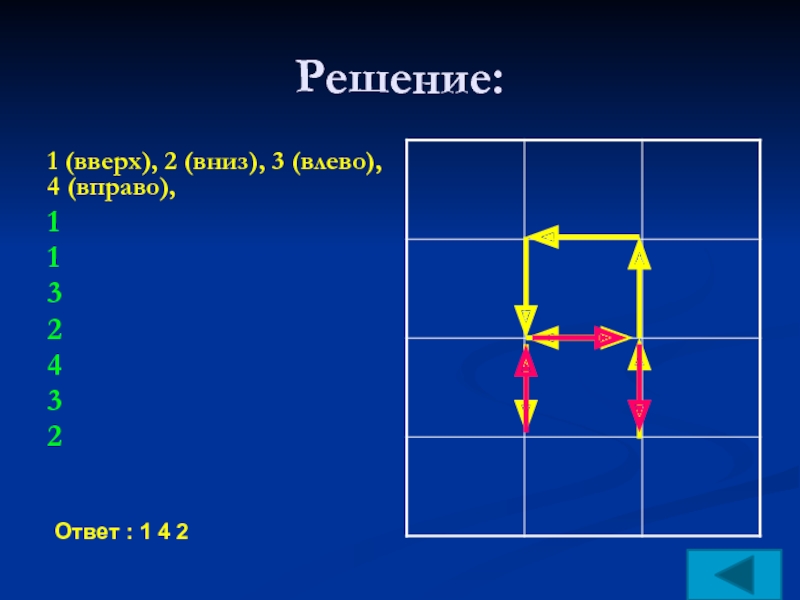
клеткам доски и может выполнять команды1 (вверх), 2 (вниз), 3 (влево), 4 (вправо),
переходя на соседнюю клетку в направлении, указанном в скобках. Если в этом направлении между клетками стоит стена, то Робот разрушается. Робот успешно выполнил программу
1132432
Какую последовательность из трех команд должен выполнить Робот, чтобы вернуться на ту клетку, где он был перед началом выполнения программы, и не разрушиться, вне зависимости от того, какие стены стоят на поле?
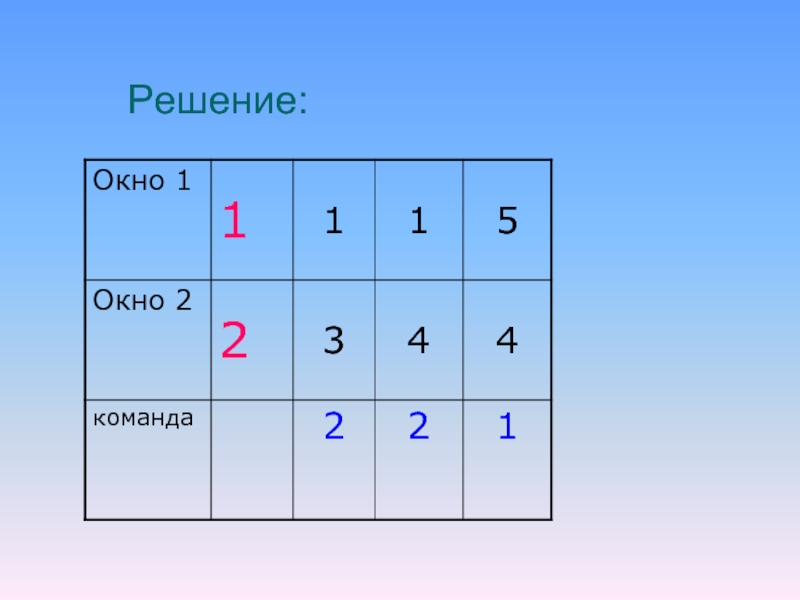
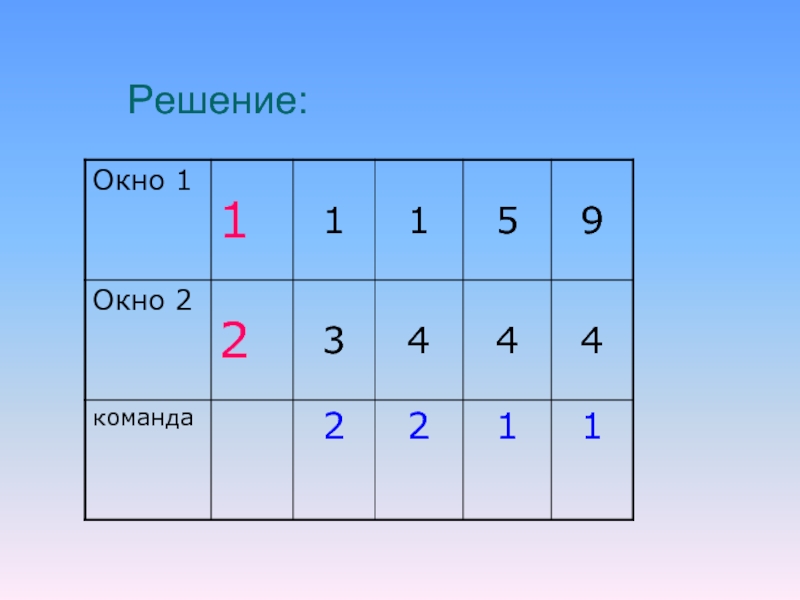
Слайд 29ЕГЭ – 2009 (В)
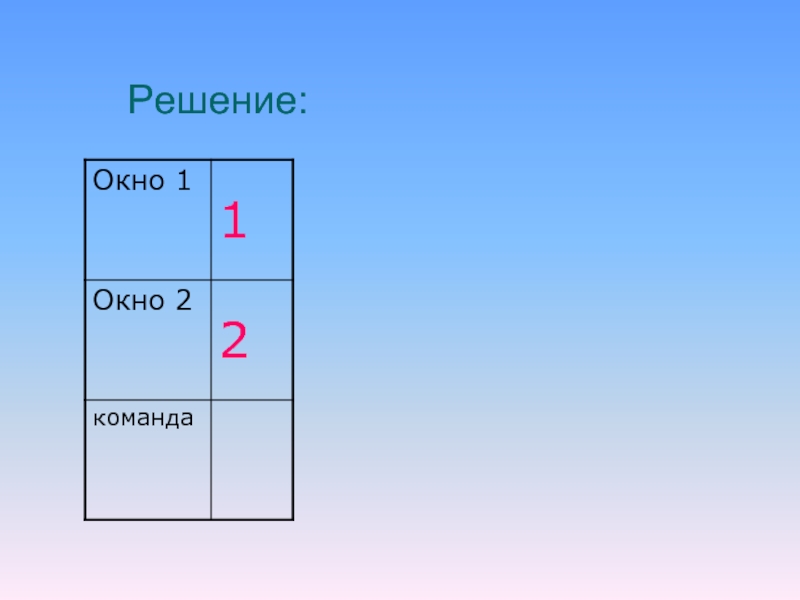
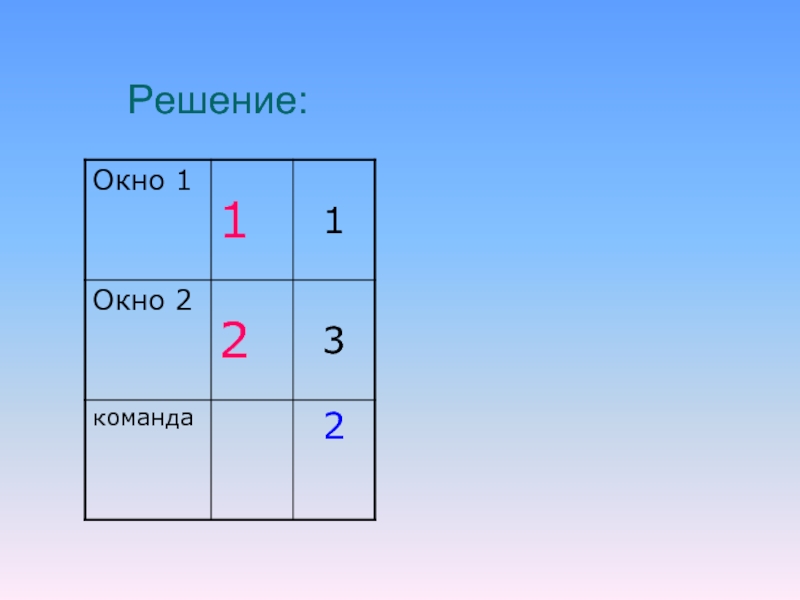
На экране есть два окна, в каждом
из которых написано по числу. У исполнителя Сумматор две команды:
Запиши
сумму чисел в первое окноЗапиши сумму чисел во второе окно.
Запишите порядок команд в программе получения из пары чисел 1 и 2 пары чисел 13 и 4, содержащей не более 5 команд.
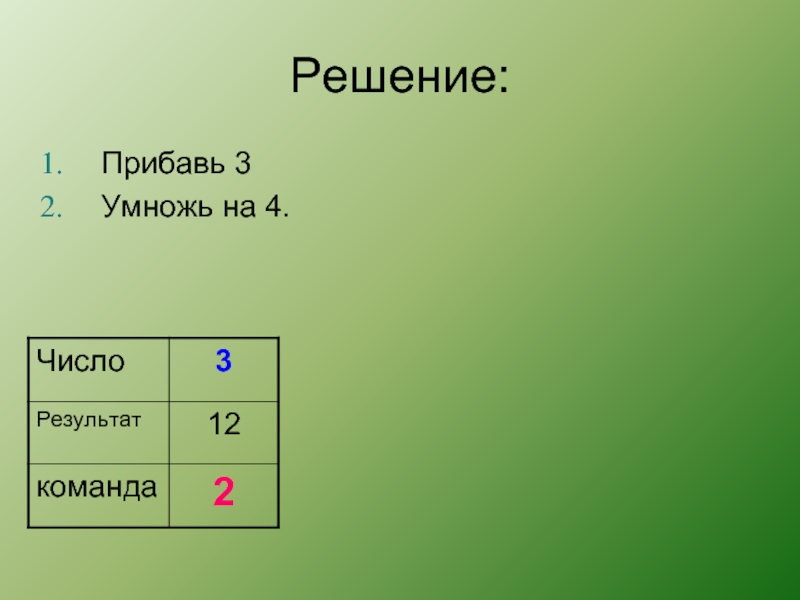
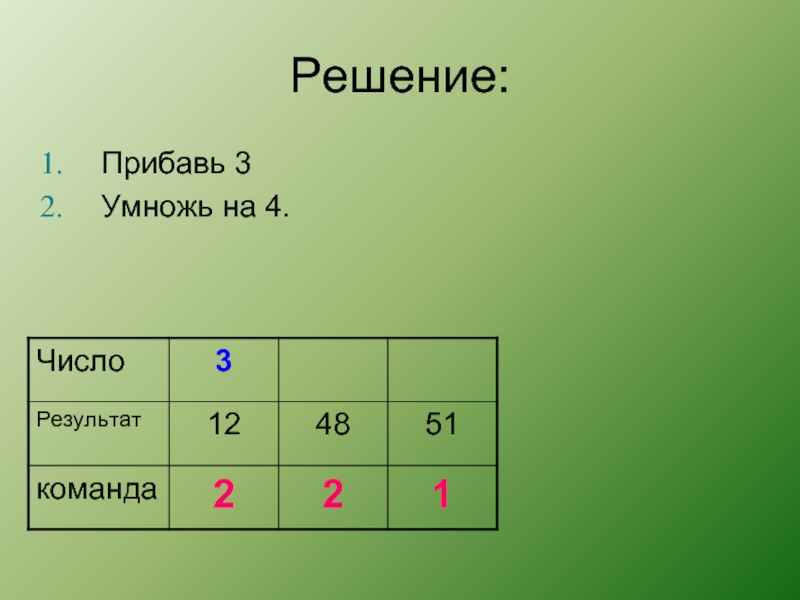
Слайд 36 ЕГЭ – 2011 (В)
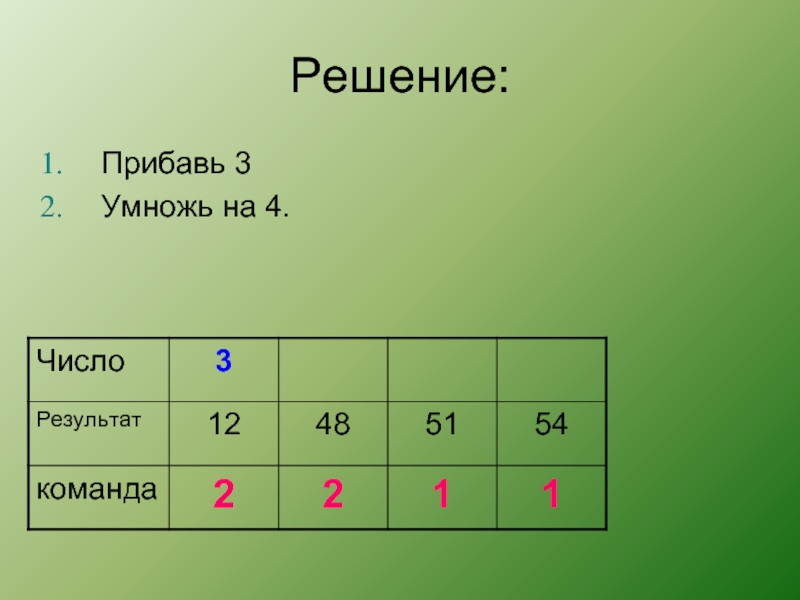
У исполнителя Калькулятор две команды, которым
присвоены номера:
Прибавь 3
Умножь на 4.
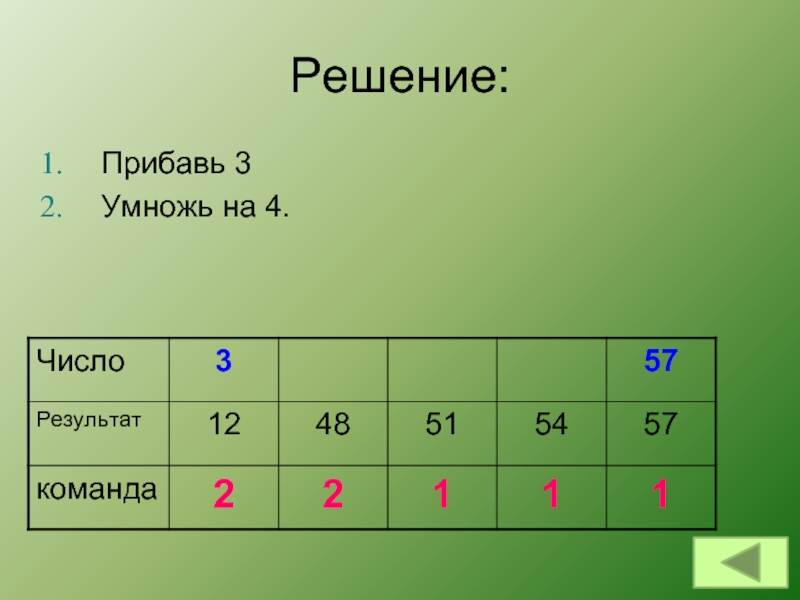
Запишите порядок команд в программе получения
из числа 3 число 57, содержащей не более 6 команд, указывая лишь номера команд. Слайд 42ЕГЭ – 2012 (В)
У исполнителя Кузнечик две команды:
1. прибавь
3,
2. вычти 2.
Первая из них увеличивает число на экране на
3, вторая – уменьшает его на 2 (отрицательные числа допускаются).Программа для Кузнечика – это последовательность команд.
Сколько различных чисел можно получить из числа 1 с помощью программы, которая содержит ровно 5 команд?
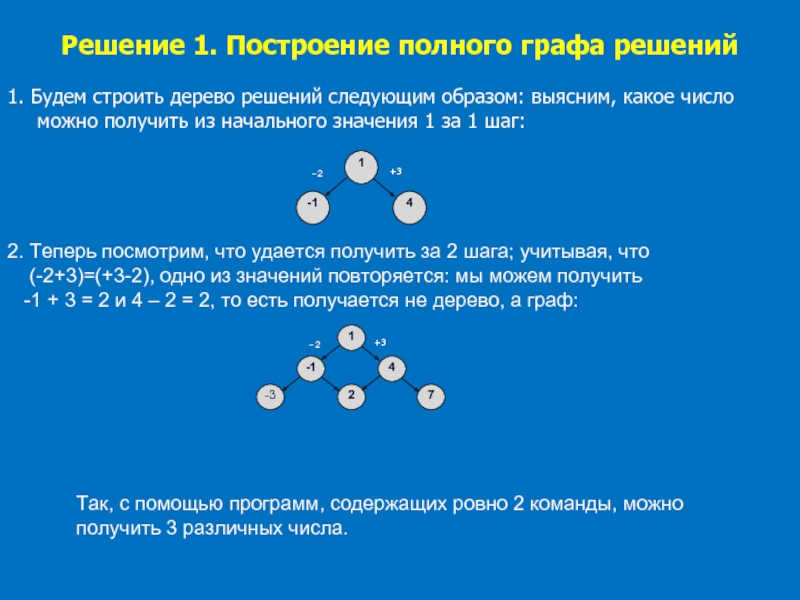
Слайд 43Решение 1. Построение полного графа решений
1. Будем строить дерево решений
следующим образом: выясним, какое число можно получить из начального значения
1 за 1 шаг:2. Теперь посмотрим, что удается получить за 2 шага; учитывая, что
(-2+3)=(+3-2), одно из значений повторяется: мы можем получить
-1 + 3 = 2 и 4 – 2 = 2, то есть получается не дерево, а граф:
Так, с помощью программ, содержащих ровно 2 команды, можно
получить 3 различных числа.
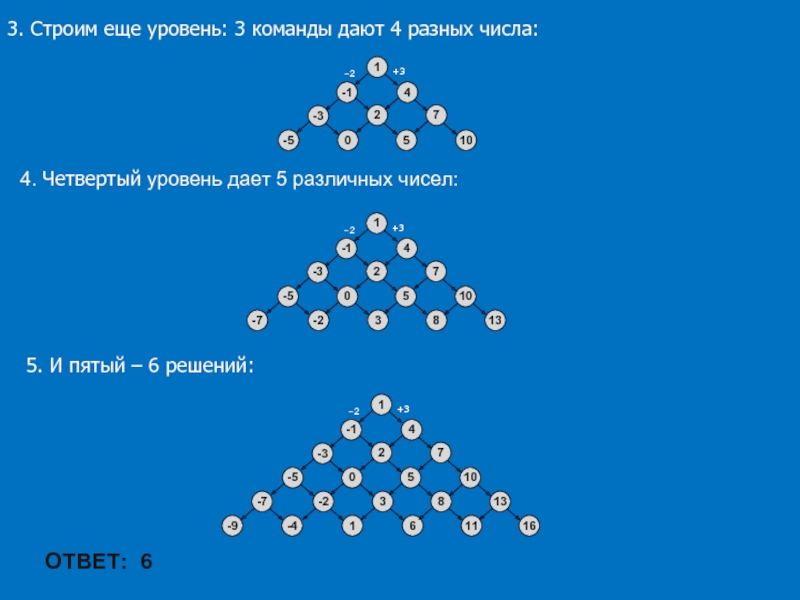
Слайд 443. Строим еще уровень: 3 команды дают 4 разных числа:
4.
Четвертый уровень дает 5 различных чисел:
5. И пятый – 6
решений:ОТВЕТ: 6
Слайд 45Решение 2. Краткий способ
Как следует из приведенных построений, если система
команд
исполнителя состоит из двух команд сложения/ вычитания,
то все
возможные программы, содержащие ровно N команд , дают N+1 различных чисел
Ответ: 6
Решение 3
Для сложения справедлив переместительный (коммутативный) закон,
значит, порядок команд в программе не имеет значения.
Поэтому существует всего 6 возможных программ, состоящих ровно
из 5 команд (с точностью до перестановки):
11111
11112
11122
11222
12222
22222
Ответ: 6.
Слайд 46Литература:
Сборник экзаменационных заданий ЕГЭ 2008- 2011 (Москва, Эксмо-2008,Интеллект-центр-2009, АСТ-2011)
Демо -
версии ЕГЭ 2005 - 2012 гг
Сайт Полякова К.Ю. (доктор технических
наук, учитель высшей категории)- http://kpolyakov.narod.ruhttp://www.fipi.ru
http://trendclub.ru/blogs/dreamrobot/6820