Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические функции на области числовых значений
Содержание
- 1. Логические функции на области числовых значений
- 2. ЗадачаЗаписать высказывание о принадлежностизначений числовой переменной Х множеству положительных чиселХ больше нуляХ >0
- 3. Отношение - логическая функция от числовых аргументов.
- 4. Предикат - логические функции от числовых аргументов.Аргументы
- 5. Пример 1Записать предикат (логическую функцию) от двух
- 6. Пример 2Записать предикат, который будет принимать значение
- 7. Пример 2Записать предикат, который будет принимать значение
- 8. Пример 2Записать предикат, который будет принимать значение
- 9. Пример 3Записать предикат, который будет принимать значение
- 10. Пример 3Записать предикат, который будет принимать значение
- 11. Пример 3Записать предикат, который будет принимать значение
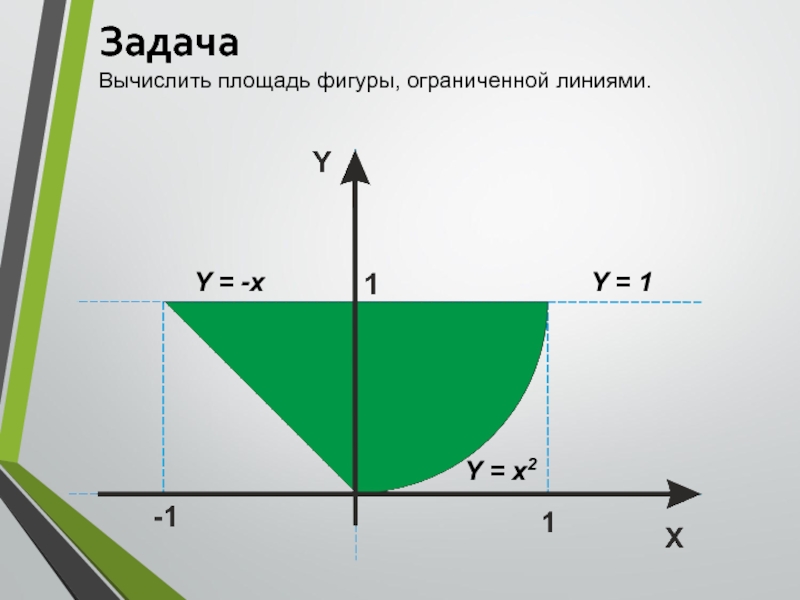
- 12. ЗадачаВычислить площадь фигуры, ограниченной линиями.
- 13. Метод Монте-КарлоМетод приближенного нахождения площадей фигур
- 14. Теория вероятностей — раздел математики, изучающий закономерности
- 15. Метод Монте-Карло можно определить как метод моделирования
- 16. Метод Монте-КарлоВо время работ над созданием водородной
- 17. Метод Монте-КарлоОдной из главных сложностей при разработке
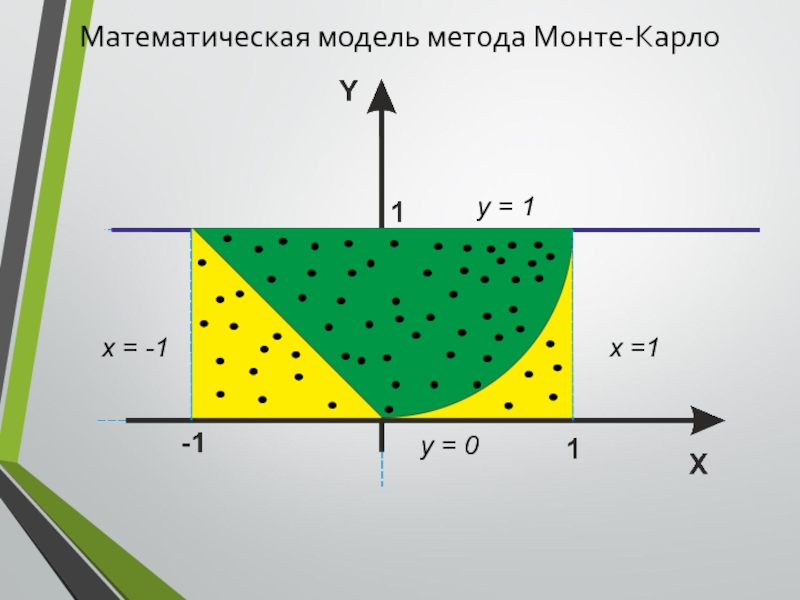
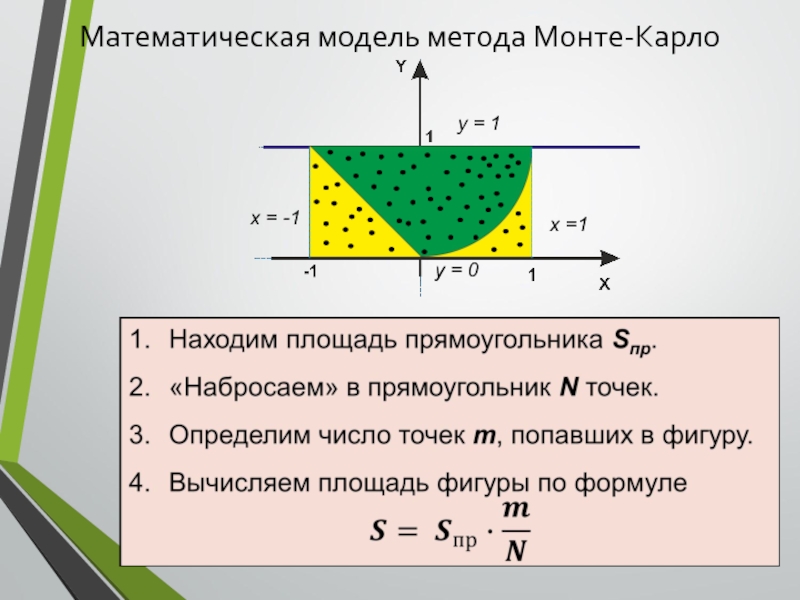
- 18. Математическая модель метода Монте-Карло
- 19. Математическая модель метода Монте-Карло
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Задача
Записать высказывание о принадлежности
значений числовой переменной Х множеству положительных чисел
Х
больше нуля
Слайд 3Отношение - логическая функция от числовых аргументов.
F(x) = (х
> 0)
Р(х, у) = (х < у).
аргументы функции
— множество действительных чисел; значения функции — множество логических величин: ИСТИНА, ЛОЖЬ.
Слайд 4Предикат - логические функции
от числовых аргументов.
Аргументы определены на бесконечном множестве
действительных чисел, а значения функции — на множестве, состоящем из
двух логических величин: ИСТИНА, ЛОЖЬ.Логические функции от числовых аргументов еще называют термином «предикат». В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы. Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.
В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы.
Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.
Слайд 5Пример 1
Записать предикат (логическую функцию) от двух вещественных аргументов х
и у, который будет принимать значение ИСТИНА, если точка с
координатами х и у на координатной плоскости лежит внутри единичной окружности с центром в начале координат.F(x, у) = (х2 + у2< 1)
Слайд 6Пример 2
Записать предикат, который будет принимать значение ИСТИНА, если точка
с координатами х и у на координатной плоскости лежит внутри
кольца с центром в начале координат и радиусами r1 и r2.r12 < х2 + у2 < r22
и
r1< r2
r1 — внутренний радиус,
r2 — внешний радиус
Слайд 7Пример 2
Записать предикат, который будет принимать значение ИСТИНА, если точка
с координатами х и у на координатной плоскости лежит внутри
кольца с центром в начале координат и радиусами r1 и r2.r22 < х2 + у2 < r12
и
r2< r1
r2 — внутренний радиус,
r1 — внешний радиус
Слайд 8Пример 2
Записать предикат, который будет принимать значение ИСТИНА, если точка
с координатами х и у на координатной плоскости лежит внутри
кольца с центром в начале координат и радиусами r1 и r2.r22 < х2 + у2 < r12 и r2< r1
F(x, у, r1, r2) = (((х2 + y2) > r12) & ((x2 + у2) < r22) & (r1 < r2)) V
(((x2 + у2) > r22) & ((x2 + у2) < r12) & (r2 < r1))
r12 < х2 + у2 < r22 и r1< r2
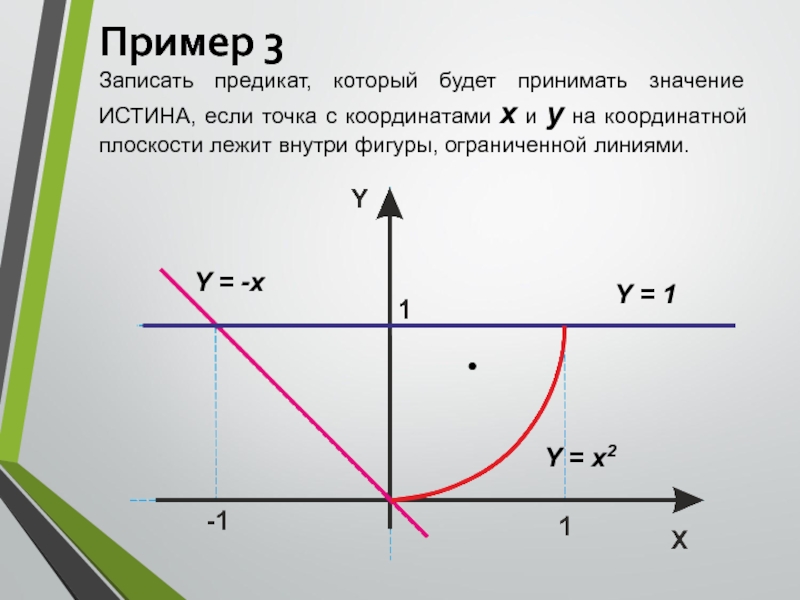
Слайд 9Пример 3
Записать предикат, который будет принимать значение ИСТИНА, если точка
с координатами х и у на координатной плоскости лежит внутри
фигуры, ограниченной линиями.Слайд 10Пример 3
Записать предикат, который будет принимать значение ИСТИНА, если точка
с координатами х и у на координатной плоскости лежит внутри
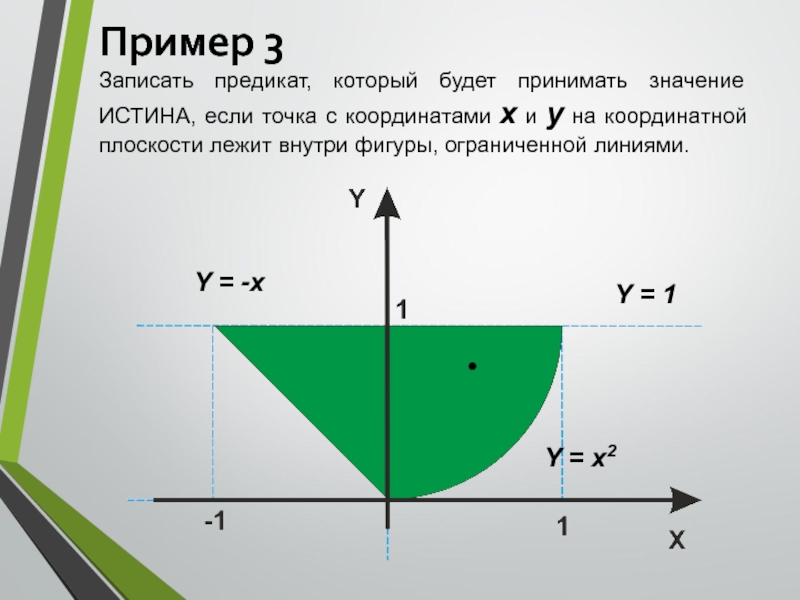
фигуры, ограниченной линиями.Слайд 11Пример 3
Записать предикат, который будет принимать значение ИСТИНА, если точка
с координатами х и у на координатной плоскости лежит внутри
фигуры, ограниченной линиями.
F(x, y) = (y > -x) & ( y< 1) & (у > x2)
Слайд 14Теория вероятностей — раздел математики, изучающий закономерности случайных явлений
Оценкой
вероятности события может служить частота его наступления в длительной серии
независимых повторений случайного эксперимента.Слайд 15Метод Монте-Карло можно определить как метод моделирования случайных величин с
целью вычисления характеристик их распределений.
Используется для решения задач в
областях физики, математики, экономики, оптимизации, теории управления и др. Граф де Буффон –
основатель метода
Метод Буффона
«бросания иглы» для определения числа
Метод Монте-Карло
Слайд 16Метод Монте-Карло
Во время работ над созданием водородной бомбы
Джон фон
Нейман и Станислав Улам разработали метод независимых статистических испытаний, известный
теперь, как метод Монте-Карло.Слайд 17Метод Монте-Карло
Одной из главных сложностей при разработке этого метода было
отсутствие в то время генераторов случайных чисел.
Тогда Нейман предложил
использовать для выработки последовательностей случайных чисел одну из рулеток в казино Монте-Карло, где были лучшие рулетки, а, следовательно, и вырабатывались лучшие последовательности случайных чисел. Военное ведомство согласилось на аренду одного из таких устройств — Улам и Нейман вдоволь наигрались за государственный счет в рулетку, а свой метод в память об этом они назвали методом Монте-Карло..