Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логика
Содержание
- 1. Логика
- 2. © Ф.А. Хафизов
- 3. © Ф.А. ХафизовЛо́гика (др.-греч. λογική — «наука
- 4. Задача логики© Ф.А. ХафизовОдна из главных задач
- 5. Современная логика© Ф.А. ХафизовВ конце XIX —
- 6. Алгебра логики © Ф.А. ХафизовРаздел математической логики,
- 7. Операции© Ф.А. Хафизов¬ - отрицание (унарная операция), /\ -
- 8. © Ф.А. ХафизовОперации отрицания (НЕ), конъюнкции (И)
- 9. Логические высказывания© Ф.А. ХафизовЛогическое высказывание — это
- 10. © Ф.А. ХафизовУпотребляемые в обычной речи слова
- 11. Таблица истинности © Ф.А. Хафизов
- 12. Логическое «отрицание» © Ф.А. Хафизов Инверсия или
- 13. Попробуйте сами составит таблицу истинности: © Ф.А.
- 14. Логическое умножение © Ф.А. Хафизов «И», конъюнкция
- 15. Таблица иcтинности© Ф.А. ХафизовВысказывание А * В
- 16. Логическое сложение © Ф.А. Хафизов «Или», дизъюнкция (лат.
- 17. Таблица истинности© Ф.А. ХафизовСтроим самостоятельно:Высказывание А v
- 18. Импликация© Ф.А. Хафизов (Лат. implico — тесно
- 19. Таблица истинности© Ф.А. ХафизовСтроим самостоятельно:Высказывание А
- 20. Эквиваленция (двойная импликация)© Ф.А. Хафизов- операция, выражаемая
- 21. Таблица истинности© Ф.А. ХафизовСтроим самостоятельно:Высказывание А
- 22. Порядок выполнения логических операций © Ф.А.
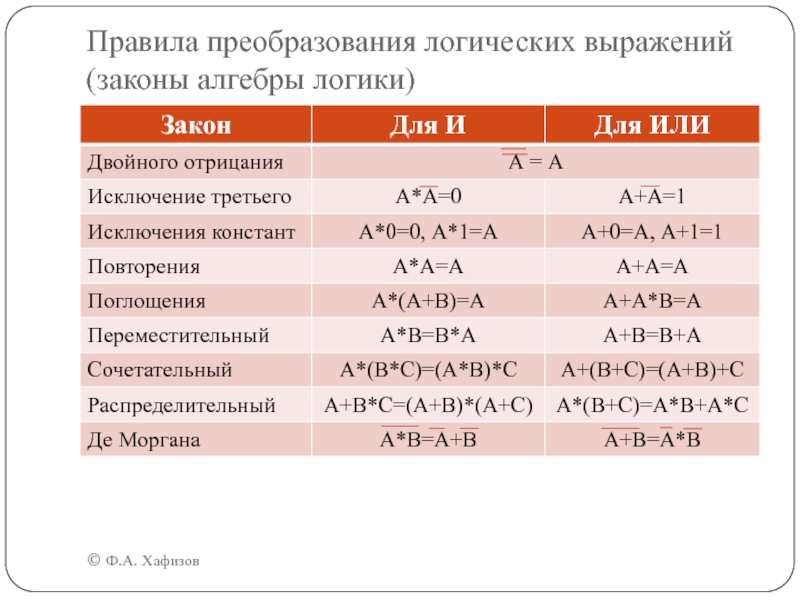
- 23. Правила преобразования логических выражений (законы алгебры логики) © Ф.А. Хафизов
- 24. © Ф.А. Хафизов
- 25. © Ф.А. Хафизов
- 26. Список использованных литературы и интернет ресурсов:© Ф.А.
- 27. Скачать презентанцию
© Ф.А. Хафизов
Слайды и текст этой презентации
Слайд 1Учитель информатики
МБОУ «Нижнечекурская сош»
Дрожжановского района
Республики Татарстан
Хафизов Фаиз Абдуллазянович
© Ф.А.
Хафизов
Слайд 3© Ф.А. Хафизов
Ло́гика (др.-греч. λογική — «наука о правильном мышлении»,
«искусство рассуждения» от λόγος — «речь», «рассуждение», «мысль») — раздел
философии, нормативная наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Логика, как наука, изучает методы достижения истины в процессе познания опосредованным путём, не из чувственного опыта, а из знаний, полученных ранее, поэтому её также можно определить как науку о способах получения выводного знания.Слайд 4Задача логики
© Ф.А. Хафизов
Одна из главных задач логики — определить,
как прийти к выводу из предпосылок (правильное рассуждение) и получить
истинное знание о предмете размышления, чтобы глубже разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления.Слайд 5Современная логика
© Ф.А. Хафизов
В конце XIX — начале XX веков
были заложены основы т. н. математической, или символической, логики. Её
суть заключается в том, что для обнаружения истинностного значения выражений естественного языка можно применять математические методы. Именно использование символической логики отличает современную логическую науку от традиционной.Огромный вклад в развитие символической логики внесли такие учёные, как Дж. Буль, О. де Морган, Г. Фреге, Ч. Пирс и др.
Слайд 6Алгебра логики
© Ф.А. Хафизов
Раздел математической логики, в котором изучаются
логические операции над высказываниями. Чаще всего предполагается, что высказывания могут
быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика.Высказывания строятся над множеством
{B, ¬,/\ ,V , 0, 1},
где B — непустое множество, над элементами которого определены три операции:
Слайд 7Операции
© Ф.А. Хафизов
¬ - отрицание (унарная операция),
/\ - конъюнкция (бинарная),
V - дизъюнкция (бинарная),
логический
ноль 0 и логическая единица 1 — константы.
Простейший и наиболее широко применяемый пример такой алгебраической
системы строится с пользованием множества B, состоящего всего из двух элементов:B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей.
Слайд 8© Ф.А. Хафизов
Операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ)
определяются в привычном нам понимании.
- эквавалетность («тогда и
только тогда, когда»),- импликация («следовательно»),
 - сложение по модулю два («исключающее или»),
- штрих Шеффера,
- стрелка Пирса и другие.
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА).
Слайд 9Логические высказывания
© Ф.А. Хафизов
Логическое высказывание — это любое повествовательное предложение,
в отношении которого можно однозначно сказать, истинно оно или ложно.
Например:
«Трава зеленая» -истинное высказывание.
«Самолет – птица» - ложное высказывание.
Всякое ли предложение является логическим высказыванием ???
Конечно нет.
Слайд 10© Ф.А. Хафизов
Употребляемые в обычной речи слова и словосочетания "не",
"и", "или", "если... , то", "тогда и только тогда" и
другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.Высказывания, образованные из других высказываний с помощью логических связок, называются составными.
Высказывания, не являющиеся составными, называются элементарными.
Слайд 11
Таблица истинности
© Ф.А. Хафизов
Это табличное представление логической
схемы (операции), в котором перечислены все возможные сочетания значений истинности
входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.Слайд 12
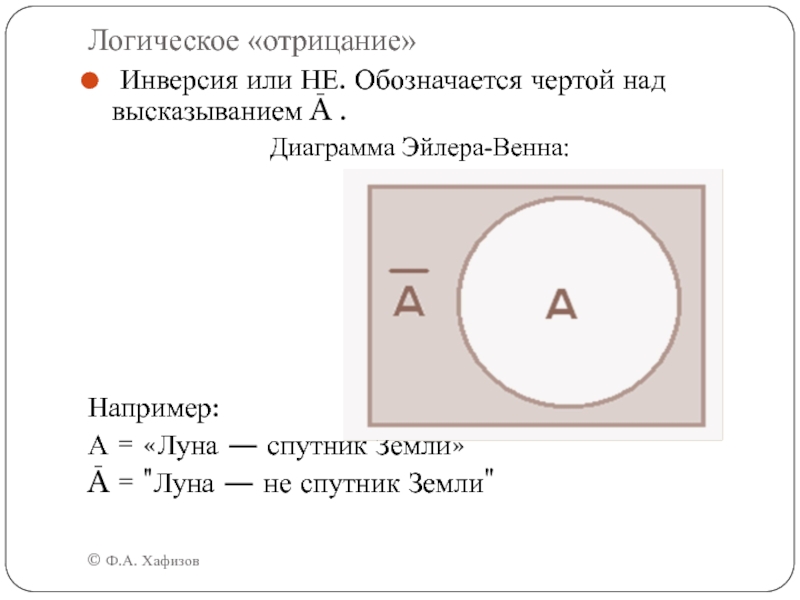
Логическое «отрицание»
© Ф.А. Хафизов
Инверсия или НЕ. Обозначается чертой над высказыванием
Ā .
Диаграмма Эйлера-Венна:
Например:
А = «Луна — спутник Земли»
Ā = "Луна
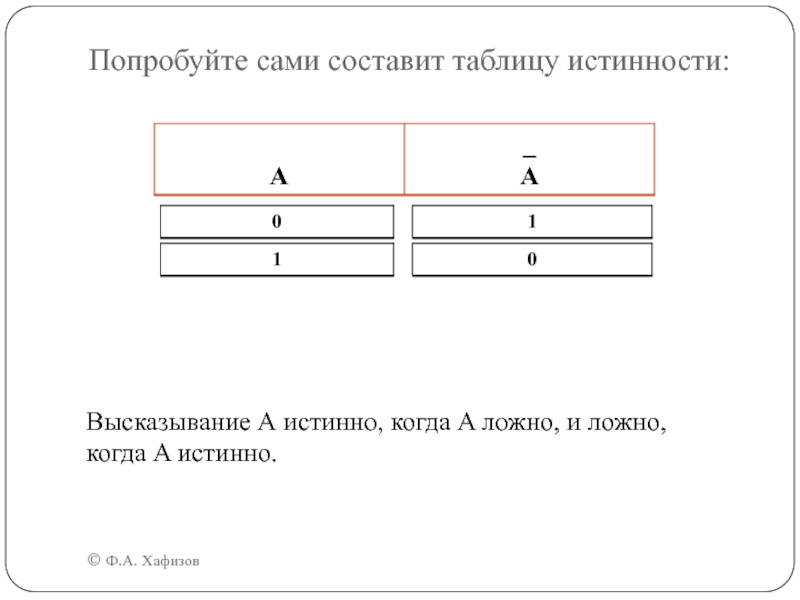
— не спутник Земли"Слайд 13Попробуйте сами составит таблицу истинности:
© Ф.А. Хафизов
Высказывание А истинно, когда
A ложно, и ложно, когда A истинно.
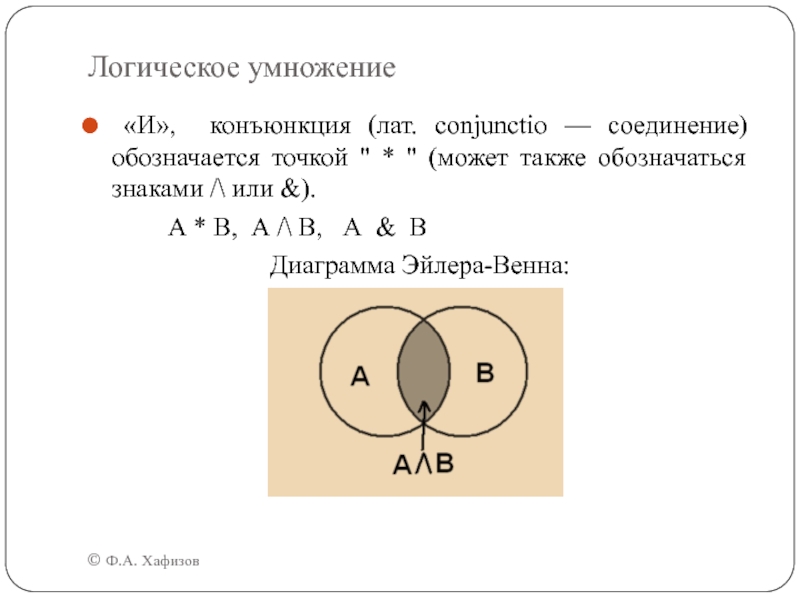
Слайд 14Логическое умножение
© Ф.А. Хафизов
«И», конъюнкция (лат. conjunctio —
соединение) обозначается точкой " * " (может также обозначаться знаками
/\ или &).А * В, А /\ В, А & В
Диаграмма Эйлера-Венна:
Слайд 15Таблица иcтинности
© Ф.А. Хафизов
Высказывание А * В истинно тогда и
только тогда, когда оба высказывания А и В истинны
Строим самостоятельно:
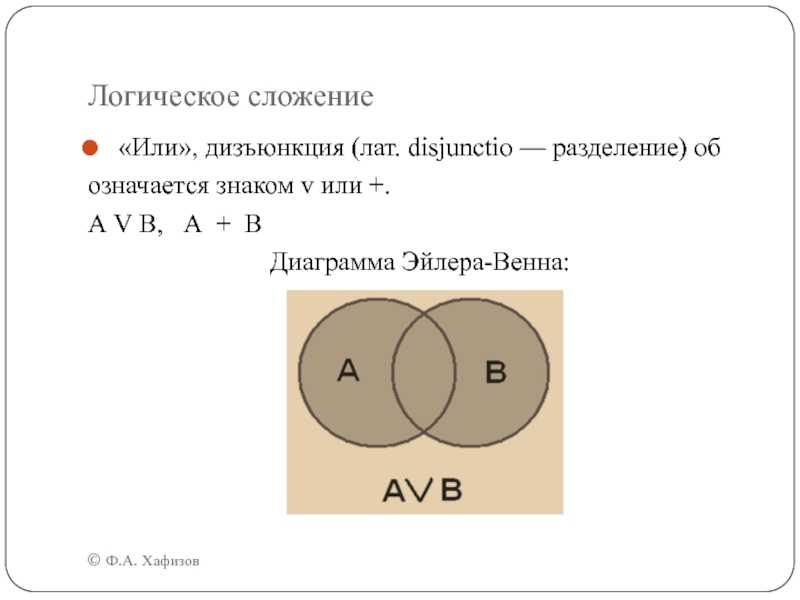
Слайд 16Логическое сложение
© Ф.А. Хафизов
«Или», дизъюнкция (лат. disjunctio — разделение)
об
означается знаком v или +.
А V В, А
+ ВДиаграмма Эйлера-Венна:
Слайд 17Таблица истинности
© Ф.А. Хафизов
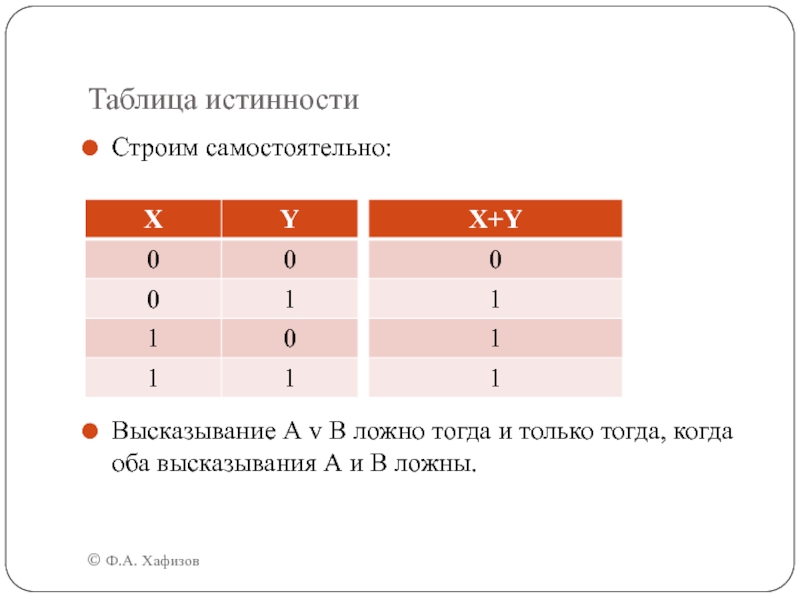
Строим самостоятельно:
Высказывание А v В ложно тогда
и только тогда, когда оба высказывания А и В ложны.
Слайд 18Импликация
© Ф.А. Хафизов
(Лат. implico — тесно связаны)
- операция,
выражаемая связками «если ..., то…», «из ... следует…», «...
влечет ...».Обозначается знаком .
А В
Слайд 19Таблица истинности
© Ф.А. Хафизов
Строим самостоятельно:
Высказывание А
В ложно тогда и только тогда, когда А истинно, а
В – ложноСлайд 20Эквиваленция (двойная импликация)
© Ф.А. Хафизов
- операция, выражаемая связками «тогда и
только тогда», «необходимо и достаточно», «... равносильно ...» Обозначается знаком
или ~.А В, А ~ В.
Слайд 21Таблица истинности
© Ф.А. Хафизов
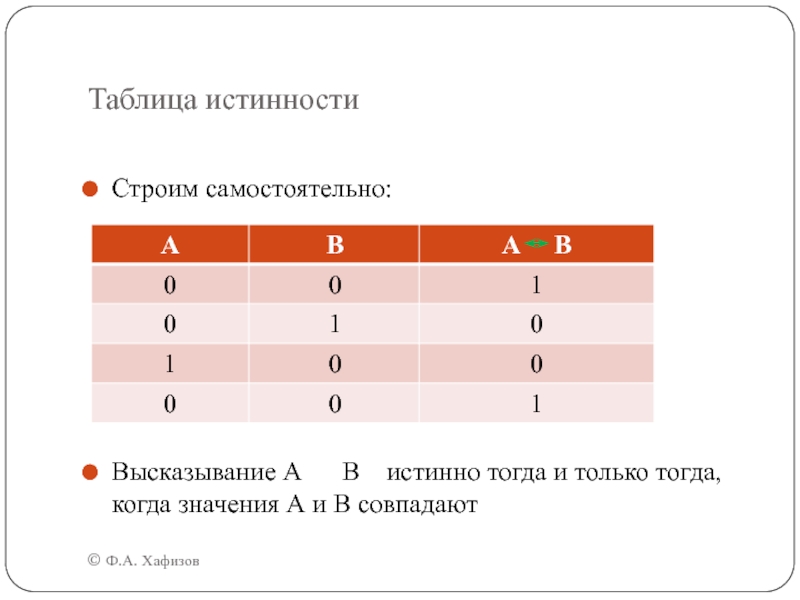
Строим самостоятельно:
Высказывание А В
истинно тогда и только тогда, когда значения А и В
совпадаютСлайд 22Порядок выполнения логических операций
© Ф.А. Хафизов
Сначала выполняется операция отрицания
(“не”),
Затем конъюнкция (“и”),
После конъюнкции — дизъюнкция (“или”),
В последнюю
очередь — импликация и эквиваленция.Слайд 26Список использованных литературы и интернет ресурсов:
© Ф.А. Хафизов
В.Ю. Лыскова, Е.А.
Ракитина Логика в информатике. — М. “Информатика и образование”. 1999
г.С.С. Коробков Элементы математической логики и теории вероятности. — Екатеринбург, 1999
М.И. Башмаков Уроки математики. Выпуск 4. Учимся логике. — Санкт-Петербург “Информатизация образования”, 2000 г.
А.П. Бойко Практикум по логике. — М. “Издательский центр АЗ”, 1997
гhttp://electrik.info/main/fakty/229-buleva-algebra-chast-1-nemnogo-istorii.html
http://www.mirea.ac.ru/d1/metodika/Indexmet.htm
http://alglib.sources.ru/articles/logic.php
http://ru.wikipedia.org/%D0%9B%D0%BE%D0%B3%D0%B8%D0%BA%D00
http://www.sch861.ru/2-school/3-11-ikt/ikt/urok/logica/2.html·
http://kpolyakov.spb.ru/school/ege.htm