Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логика. Решение экзаменационных задач
Содержание
- 1. Логика. Решение экзаменационных задач
- 2. Немного теории…Алгебра логики – это раздел математики,
- 3. Логические операцииОперация отрицания 2) Логическое умножение (конъюнкция)3) Логическое сложение (дизъюнкция)
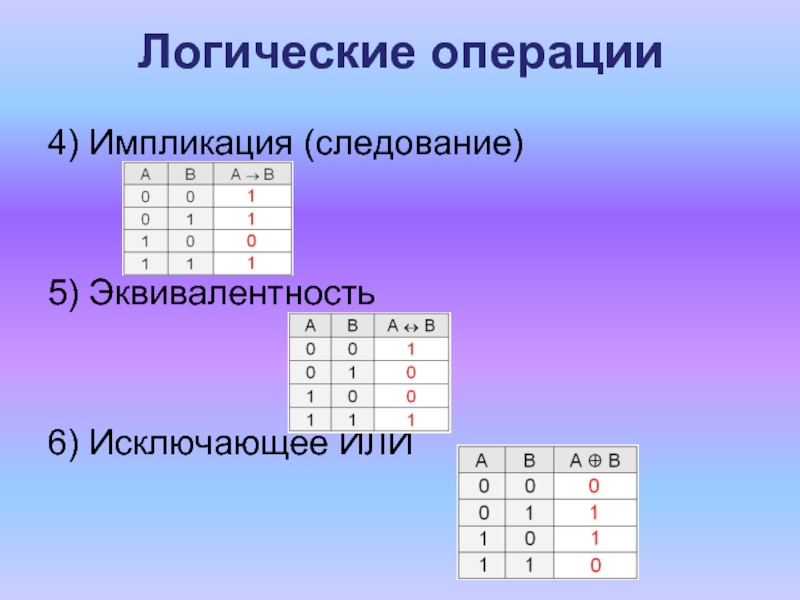
- 4. Логические операции4) Импликация (следование)5) Эквивалентность6) Исключающее ИЛИ
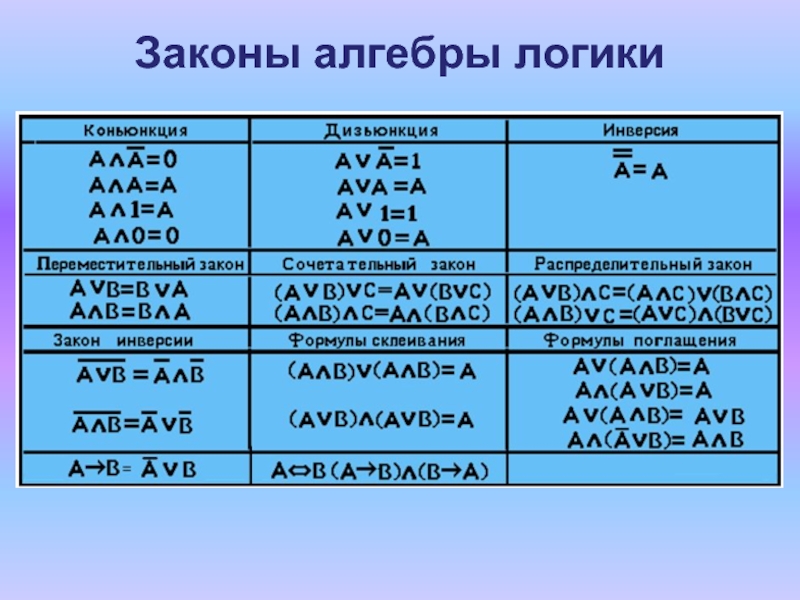
- 5. Законы алгебры логики
- 6. Решение задач
- 7. Задача №1Для какого числа X истинно высказывание:((x
- 8. Задача №2Для какого имени ложно высказывание:(первая буква
- 9. Задача №3Построить таблицу истинности для следующей функции:F(X,Y,Z)=(x→y)·z
- 10. Задача №4Символом F обозначено одно из указанных
- 11. Задача №5Какое логическое выражение равносильно выражению:Решение: применим
- 12. Задача №6Каково наименьшее натуральное число X, при
- 13. Задача №7Найдите все тройки значения L,M,N, при
- 14. Задача №8В таблице приведены запросы к поисковому
- 15. Задача №8Решение:Воспользуемся кругами Эйлера (диаграммами Вена):Ответ: 4123.задания
- 16. Задача №9В табличной форме представлен фрагмент базы
- 17. Задача №9Решение:Первому условию Пол=’м’ удовлетворяют записи №2,
- 18. Задания1) Для какого числа X истинно высказывание:
- 19. Задания1) Для какого имени истинно высказывание:
- 20. ЗаданияЗаполните таблицу истинности логическихвыражений:1)2)3)
- 21. ЗаданияСимволом F обозначено одно из указанных ниже
- 22. Задания1) Какое логическое выражение равносильно выражению:2) Какое логическое выражение равносильно выражению:3) Какое логическое выражение равносильно выражению:
- 23. Задания1) Каково наименьшее натуральное число X, при
- 24. Задания 1) Найдите значения логических A,B,C,D,
- 25. ЗаданияВ таблицах приведены запросы к поисковому серверу:1)
- 26. ЗаданияНиже в табличной форме представлен фрагмент базы
- 27. Задания2) В таблице приведены данные о составе
- 28. Источники материалов:http://s99-omsk.narod.ru/pupil/vip/i2003/i2003/logika/be.gifhttp://school.sgu.ruП. А. Якушкин, С. С. Крылов,
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Логика. Решение экзаменационных задач.
Автор: учитель информатики и ИКТ
МБОУ
«СОШ №9» г. Энгельса
Слайд 2Немного теории…
Алгебра логики – это раздел математики, изучающий высказывания со
стороны их логических значений истинности или ложности.
Высказывание – это повествовательное
предложение, относительно которого можно сказать истинно оно или ложно.Пример:
Москва – это столица России
Сейчас идет снег
Растения не выделяют кислород
Слайд 3Логические операции
Операция отрицания
2) Логическое умножение (конъюнкция)
3) Логическое сложение
(дизъюнкция)
Слайд 7Задача №1
Для какого числа X истинно высказывание:
((x
4)4
Решение:
Подставляем в выражение предложенные варианты ответа и определяем, истинно выражение
или ложно:1) x=1: ((1<4)→(1<3))^((1<3)→(1<1))=(1→1)^(1→0)
Сначала вычислим выражение в скобках:
(1→1)^(1→0)=1^0=0 (не подходит)
Аналогично подставляем другие варианты ответа, вычисляем:
2) x=2: ((2<4)→(2<3))^((2<3)→(2<1))=(1→1)^(1→0)=1^0=0 (не подходит)
3) x=3: ((3<4)→(3<3))^((3<3)→(3<1))=(1→0)^(0→0)=0^1=0 (не подходит)
4) x=4: ((4<4)→(4<3))^((4<3)→(4<1))=(0→0)^(0→0)=1^1=1 (подходит)
Ответ: 4.
задания
Слайд 8Задача №2
Для какого имени ложно высказывание:
(первая буква гласная ^последняя буква
согласная)→ ¬(третья буква согласная)?
Дмитрий 2) Антон 3) Екатерина 4) Анатолий
Решение:
Подставляем
в выражение предложенные варианты ответа и определяем, истинно выражение или ложно:Дмитрий: (0 ^ 1)→ ¬(0)=0→1 = 1 (не подходит)
Антон: (1 ^ 1)→ ¬(1)=1→0 = 0 (подходит)
Екатерина: (1 ^ 0)→ ¬(0)=0→1 = 1 ( не подходит)
Анатолий: (1 ^ 1)→ ¬(0)=1→1 = 1 ( не подходит)
Ответ: 2.
задания
Слайд 9Задача №3
Построить таблицу истинности для следующей функции:
F(X,Y,Z)=(x→y)·z + ¬y
Решение:
1) Нарисуем
таблицу на K строк, где K=2n, n - количество
высказываний в
функцииN=3, k=8 строк
2) Запишем в таблице все варианты X,Y,Z и вычисляем выражение по
действиям:
задания
Слайд 10Задача №4
Символом F обозначено одно из указанных ниже
логических выражений от
3-х аргументов X,Y,Z. Дан
фрагмент таблицы истинности выражения F.
Какое выражение соответствует
F?Решение:
Подставляем значения X,Y,Z из таблицы в предложенные варианты ответа,
сравниваем со значением F(X,Y,Z):
Ответ: 4
задания
Слайд 11Задача №5
Какое логическое выражение равносильно выражению:
Решение: применим отрицание к выражению
в скобках в соответствии с законом инверсии:
Ответ: 2.
задания
Слайд 12Задача №6
Каково наименьшее натуральное число X, при котором
истинно высказывание
Решение: Импликация ложна, когда первое выражение истинно, а второе ложно(см.
таблицы истинности). Во всех остальных случаях импликация истинна. Первое выражение ложно для всех натуральных x>10 и истинно для всех натуральных x<11. Второе выражение истинно для всех натуральных x>9 и ложно для всех натуральных x<10. Следовательно, данная импликация истинна для всех натуральных x>9. Наименьшее число, соответствующее этому условию x=10.Ответ: 10.
задания
Слайд 13Задача №7
Найдите все тройки значения L,M,N, при которых указанное выражение
принимает ложное значение.
Решение:
Из таблицы истинности импликации получаем, что L=0, а
Подставляем полученное значение L в выражение в скобках:
Из таблицы истинности дизъюнкции следует,
что выражение истинно тогда и только тогда, когда
(M=1, N=0) или (M=0, N=1) или (M=1, N=1). Поскольку L=0,
ответом будут все тройки (L=0, M=1, N=0), (L=0, M=0, N=1),
(L=0,M=1, N=1).
Ответ: (L=0, M=1, N=0), (L=0, M=0, N=1), (L=0, M=1, N=1).
задания
Слайд 14Задача №8
В таблице приведены запросы к поисковому серверу:
Расположите номера запросов в порядке возрастания количества страниц, которые
найдёт поисковый сервер по каждому запросу.Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» − &.
Слайд 16Задача №9
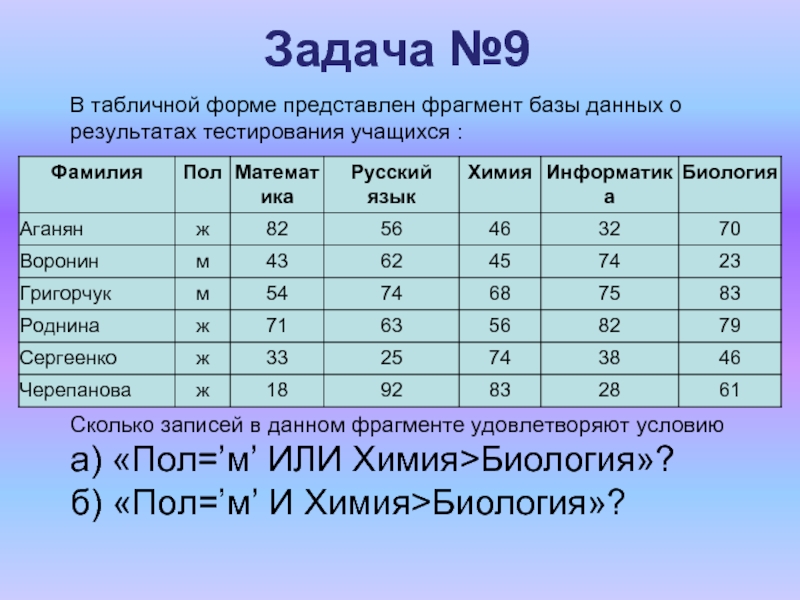
В табличной форме представлен фрагмент базы данных о результатах
тестирования учащихся :
Сколько записей в данном фрагменте удовлетворяют условию
а) «Пол=’м’
ИЛИ Химия>Биология»?б) «Пол=’м’ И Химия>Биология»?
Слайд 17Задача №9
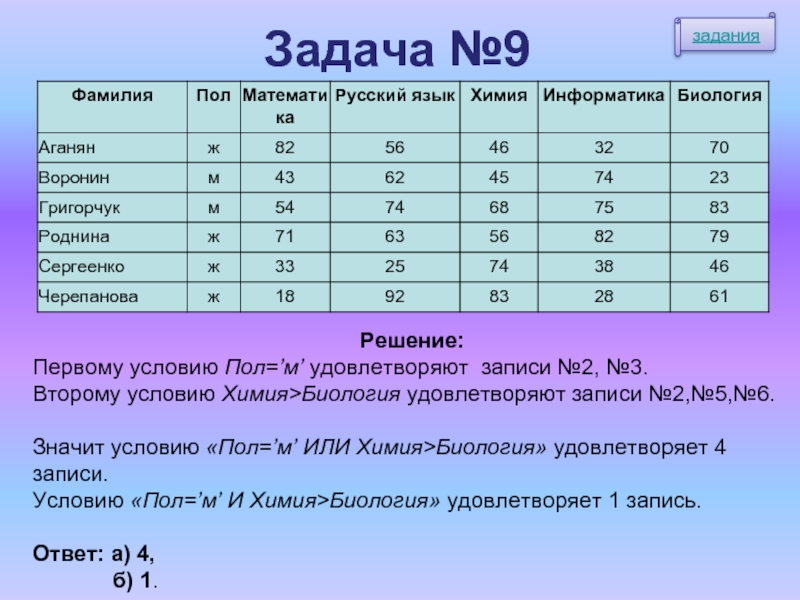
Решение:
Первому условию Пол=’м’ удовлетворяют записи №2, №3.
Второму условию Химия>Биология
удовлетворяют записи №2,№5,№6.
Значит условию «Пол=’м’ ИЛИ Химия>Биология» удовлетворяет 4 записи.
Условию
«Пол=’м’ И Химия>Биология» удовлетворяет 1 запись.Ответ: а) 4,
б) 1.
задания
Слайд 18Задания
1) Для какого числа X истинно высказывание:
1)1 2)3 3)4 4)2
2) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
3) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
4) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
5) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
Слайд 19Задания
1) Для какого имени истинно высказывание:
1)
КСЕНИЯ 2) ЮЛИЯ 3) ПЕТР 4) АЛЕКСЕЙ
2) Для
какого имени истинно высказывание:1) Антон 2) Федор 3) Елена 4) Вадим
Для какого имени истинно высказывание:
1) Иван 2) Петр 3) Елена 4) Павел
4) Для какого слова ложно высказывание:
1) кенгуру 2) антилопа 3) ящерица 4) крокодил
5) Для какого слова истинно высказывание:
1) гаоцин 2) скворец 3) ласточка 4) моёвка
Слайд 21Задания
Символом F обозначено одно из указанных ниже логических выражений от
3-х
аргументов X,Y,Z. Дан фрагмент таблицы истинности выражения F.
Какое выражение соответствует
F?1)
2)
3)
Слайд 22Задания
1) Какое логическое выражение равносильно выражению:
2) Какое логическое выражение равносильно
выражению:
3) Какое логическое выражение равносильно выражению:
Слайд 23Задания
1) Каково наименьшее натуральное число X, при котором
истинно высказывание
2) Каково
наибольшее целое число X, при котором
ложно высказывание
3) Каково наибольшее целое
число X, при которомистинно высказывание
4) Каково наибольшее целое число X, при котором
ложно высказывание
5) Каково наибольшее целое число X, при котором
истинно высказывание
Слайд 24Задания
1) Найдите значения логических A,B,C,D, при которых указанное
логическое выражение ложно. Ответ запишите в виде строки из четырех
символов: значений переменных A,B,C,D (в указанном порядке). Так, например, строка 0101 соответствует тому, что A=0, B=1, C=0, D=1.a)
b)
2) Сколько различных решений имеет уравнение
где K, L, M, N - логические переменные?
Слайд 25Задания
В таблицах приведены запросы к поисковому серверу:
1)
Расположите номера запросов
в порядке возрастания количества
страниц, которые найдёт поисковый сервер по каждому
запросу. 2)
Расположите номера запросов в порядке убывания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
3)
Расположите номера запросов в порядке возрастания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
Слайд 26Задания
Ниже в табличной форме представлен фрагмент базы данных о погоде.
a)
Сколько записей в данном фрагменте удовлетворяют условию
(Осадки=«дождь») ИЛИ (давление
750)?б) Сколько записей в данном фрагменте удовлетворяют условию
(Осадки=«дождь») И (давление ≤ 750)?
К следующему заданию
Слайд 27Задания
2) В таблице приведены данные о составе и калорийности некоторых
продуктов:
Сколько записей в данной таблице удовлетворяют условию:
Вода>85 ИЛИ (белки+углеводы
И ккал>38) ?
Слайд 28Источники материалов:
http://s99-omsk.narod.ru/pupil/vip/i2003/i2003/logika/be.gif
http://school.sgu.ru
П. А. Якушкин, С. С. Крылов, ЕГЭ 2010. Информатика:
сборник экзаменационных заданий. М.: Эксмо, 2009
П. А. Якушкин, В.
Р. Лещинер, Информатика: типовые тестовые задания. М.: Экзамен, 2012 Л. Н. Евич, С. Ю. Кулабухов, Информатика и ИКТ. 10-11 классы. Тематические тесты. Подготовка к ЕГЭ. Базовый, повышенный, высокий уровни: типовые тестовые задания. Ростов-на-Дону: Легион - М, 2011
Демонстрационный вариант контрольных измерительных материалов для проведения в 2012 году государственной (итоговой) аттестации (в новой форме) по ИНФОРМАТИКЕ и ИКТ