Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Высказывание. Логические операции
Содержание
- 1. Высказывание. Логические операции
- 2. Высказывание- предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.ВысказываниеИстинное (1)Ложное (0)
- 3. ВысказываниеВ русском языке высказывания выражаются повествовательными предложениями:Побудительные
- 4. ВысказываниеПростое высказываниеСложное высказываниеБуква «А» - гласнаяБуква «А»
- 5. Логическая переменнаяэто простое высказывание, содержащее только одну
- 6. Таблица истинностиОбозначениеЛогические операцииИнверсия- (отрицание) делает истинное высказывание ложным, а ложное истинным.
- 7. Таблица истинностиОбозначениеЛогические операцииКонъюнкция - логическое умножение (союз
- 8. Таблица истинностиОбозначениеЛогические операцииДизъюнкция - логическое сложение (союз
- 9. Таблица истинностиОбозначениеЛогические операцииИмпликация - (логическое следование -
- 10. Таблица истинностиОбозначениеЛогические операцииЭквиваленция - (логическое равенство -
- 11. Последовательность операцийИнверсия ¬Конъюнкция /\Дизъюнкция \/Эквиваленция ↔, импликация →Приоритет операций можно изменить при помощи скобок
- 12. Решение задачСоставить таблицу истинности для выражения: 100100111001F= ¬ A ∨ B ∧ A
- 13. Решение задачСоставить таблицу истинности для выражения: 110000111001F= (¬ A ∨ B) ∧ (B → A)1111
- 14. Решение задачДля какого из приведённых значений числа X истинно высказывание: (X < 7) И НЕ (X
- 15. Решение задачДля какого из приведённых чисел истинно
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Высказывание
- предложение на любом языке, содержание которого можно однозначно определить
как истинное или ложное.
Слайд 3Высказывание
В русском языке высказывания выражаются повествовательными предложениями:
Побудительные и вопросительные предложения
высказываниями не являются.
В русском алфавите 33 буквы
Цифра 2 является четной
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?
Слайд 4Высказывание
Простое высказывание
Сложное высказывание
Буква «А» - гласная
Буква «А» - гласная И
буква «Е»
Сложные высказывания состоят из простых высказываний, соединенных логическими связками:
Слайд 5Логическая переменная
это простое высказывание, содержащее только одну мысль. Ее символическое
обозначение — латинская буква (например A, B, X, Y и
т. д. ).А – «Буква «А» - гласная»
B – «Кошка является домашним животным»
Слайд 6Таблица истинности
Обозначение
Логические операции
Инверсия- (отрицание) делает истинное высказывание ложным, а ложное
истинным.
Слайд 7Таблица истинности
Обозначение
Логические операции
Конъюнкция - логическое умножение (союз и), при котором
составное высказывание истинно тогда и только тогда, когда истинны все
входящие в него простые высказывания.Слайд 8Таблица истинности
Обозначение
Логические операции
Дизъюнкция - логическое сложение (союз или), при котором
составное высказывание ложно тогда, когда ложны все входящие в него
простые высказывания.Слайд 9Таблица истинности
Обозначение
Логические операции
Импликация - (логическое следование - если…, то…). Ложно
тогда и только тогда, когда из истинного высказывания следует ложное.
x
→ yСлайд 10Таблица истинности
Обозначение
Логические операции
Эквиваленция - (логическое равенство - тогда и только
тогда…). Истинно тогда и только тогда, когда оба высказывания истины
или оба ложны.x ↔ y
Слайд 11Последовательность операций
Инверсия ¬
Конъюнкция /\
Дизъюнкция \/
Эквиваленция ↔, импликация →
Приоритет операций можно
изменить при помощи скобок
Слайд 13Решение задач
Составить таблицу истинности для выражения:
1
1
0
0
0
0
1
1
1
0
0
1
F= (¬ A ∨
B) ∧ (B → A)
1
1
1
1
Слайд 14Решение задач
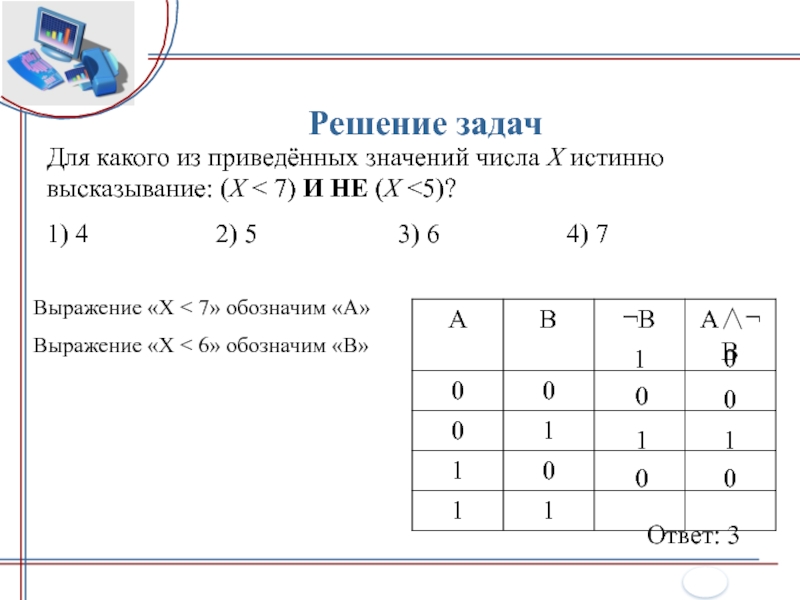
Для какого из приведённых значений числа X истинно высказывание: (X < 7) И НЕ (X
1) 4
2) 5 3) 6 4) 7Выражение «X < 7» обозначим «А»
Выражение «X < 6» обозначим «В»
1
1
0
0
0
0
0
1
Ответ: 3
Слайд 15Решение задач
Для какого из приведённых чисел истинно высказывание:
НЕ (число < 100) И НЕ (число
чётное)?
1) 123 2) 106 3) 37 4) 8
Выражение «число < 100» обозначим «А»
Выражение «число
четное» обозначим «В»1
1
0
0
0
0
0
1
1
0
1
0
Ответ: 1