Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование фракталов в среде Maxima 9 класс
Содержание
- 1. Моделирование фракталов в среде Maxima 9 класс
- 2. MaximaMaxima — система для работы с символьными и
- 3. Профессор Уильям Шелтер из Техасского университета в Остине поддерживал
- 4. Термин «фрактал» введён Бенуа Мандельбротом в 1975 году и получил широкую
- 5. Что такое фракталы Фрактал - это геометрическая
- 6. В живой природе:КораллыМорские звезды и ежиМорские раковиныЦветы и растения
- 7. Слайд 7
- 8. Обладает сложной структурой при любом увеличении;Является (приближенно)
- 9. треугольник Серпинского, фракталы «Дерево», «Папоротник»; множество Мандельброта
- 10. Функции пакета fractals
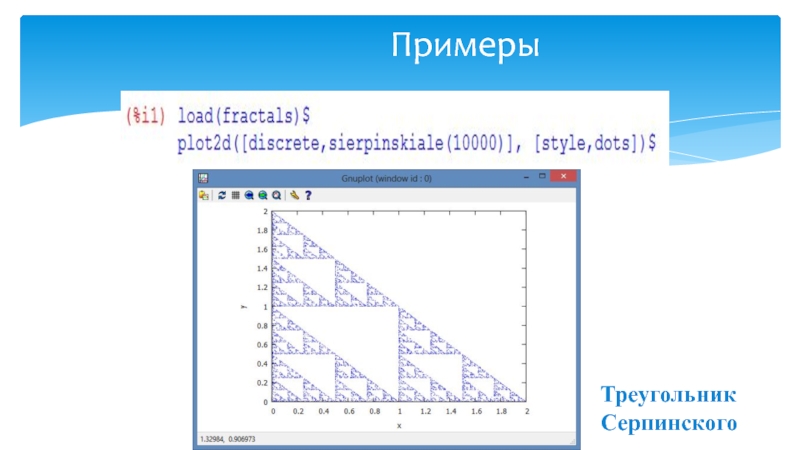
- 11. ПримерыТреугольник Серпинского
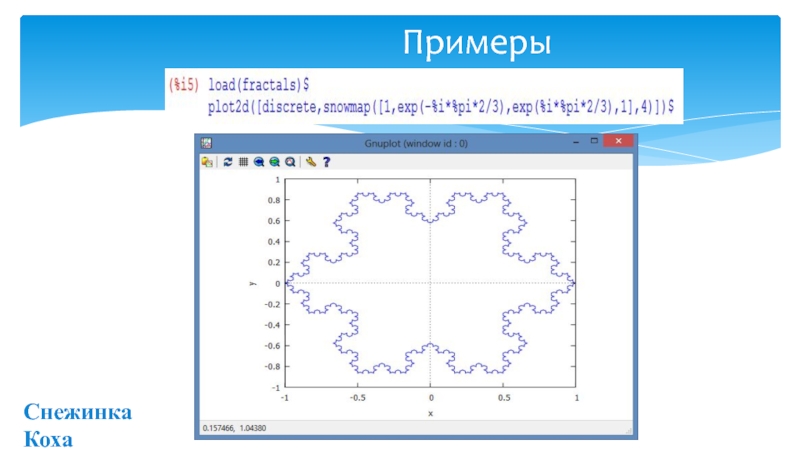
- 12. ПримерыСнежинка Коха
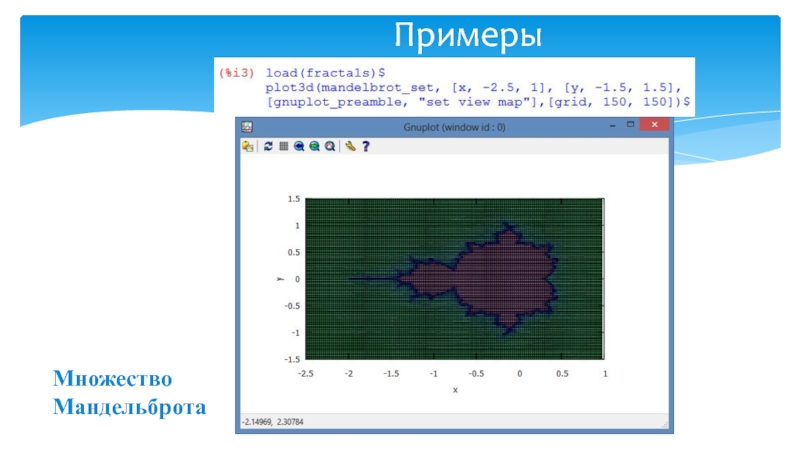
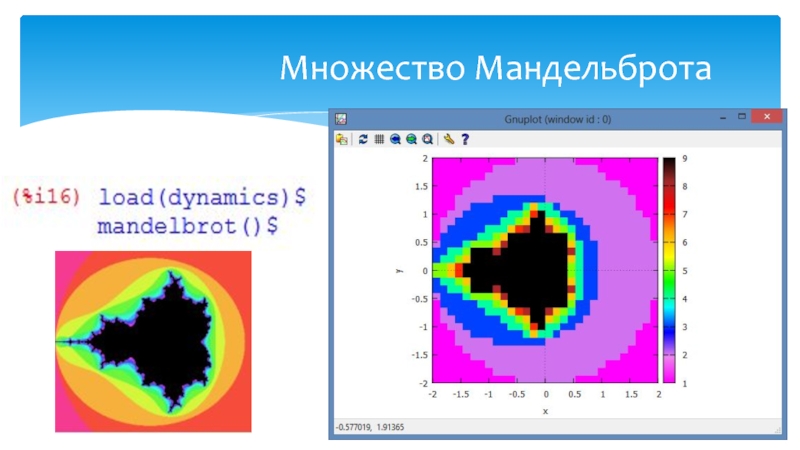
- 13. ПримерыМножество Мандельброта
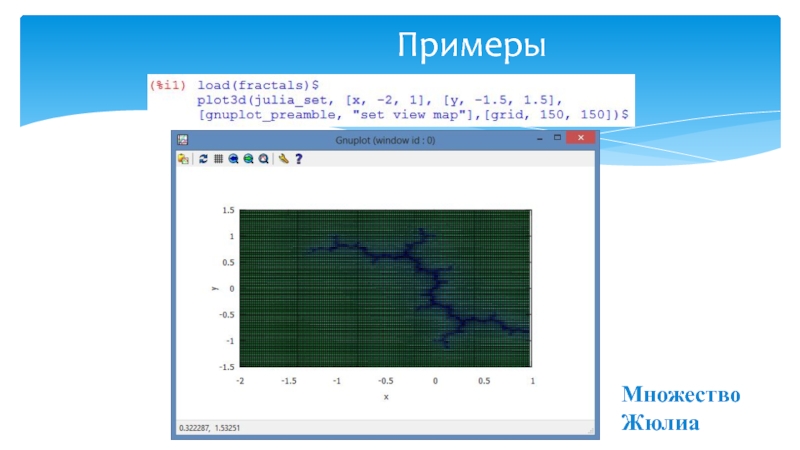
- 14. ПримерыМножество Жюлиа
- 15. Гастон Морис Жюлиа (1893—1978) — французский математик, открывший множество Жюлиа.
- 16. паутинная диаграмма;бифуркационная диаграмма;эволюция орбиты одно- и двумерного
- 17. Функции пакета dynamics
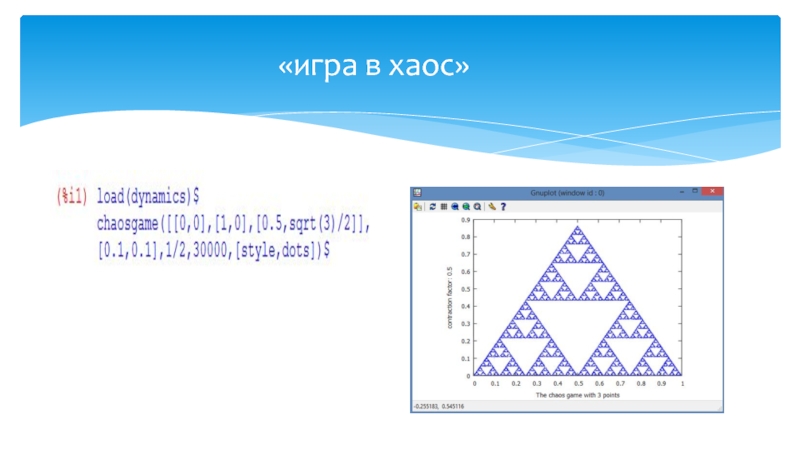
- 18. «игра в хаос»
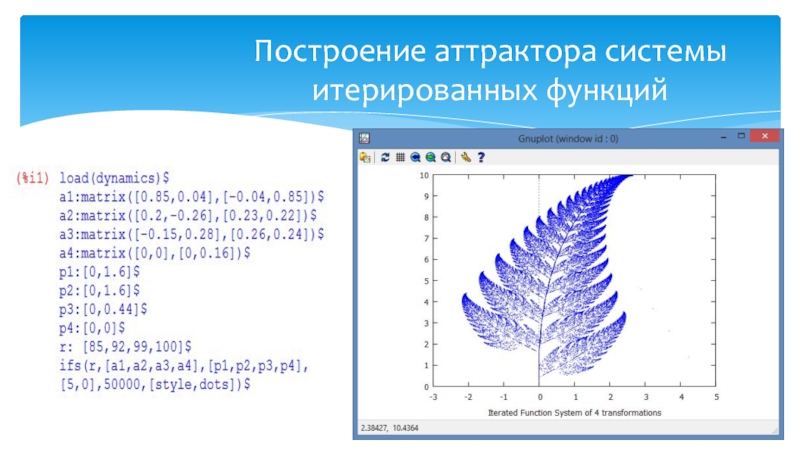
- 19. Построение аттрактора системы итерированных функций
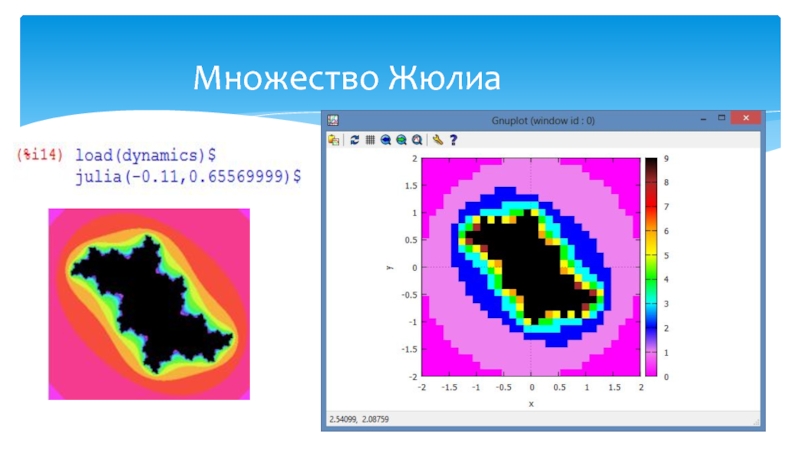
- 20. Множествo Жюлиа
- 21. Множество Мандельброта
- 22. Слайд 22
- 23. Скачать презентанцию
MaximaMaxima — система для работы с символьными и численными выражениями, включающая дифференцирование, интегрирование, разложение в ряд, преобразование Лапласа, обыкновенные дифференциальные уравнения, системы линейных уравнений, многочлены, множества, списки, векторы, матрицы и тензоры.
Слайды и текст этой презентации
Слайд 3Профессор Уильям Шелтер из Техасского университета в Остине поддерживал один из вариантов
системы, известный как DOE Macsyma, с 1982 года до самой своей смерти в 2001
году.Из истории
Слайд 4Термин «фрактал» введён Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом
в 1977 году его книги «Фрактальная геометрия природы».
Фрактал (от латинского слова fractus,
что означает разбитый, поделенный на части)
Слайд 5Что такое фракталы
Фрактал - это геометрическая фигура, состоящая из
частей и которая может быть поделена на части, каждая из
которых будет представлять уменьшенную копию целого.
Слайд 6В живой природе:
Кораллы
Морские звезды и ежи
Морские раковины
Цветы и растения (брокколи, капуста)
Кроны деревьев и листья
растений
Плоды (ананас)
Кровеносная система и бронхи людей и животных
Природные объекты, обладающие фрактальными свойствами
В неживой
природе:Границы географических объектов (стран, областей, городов)
Береговые линии
Горные хребты
Снежинки
Облака
Молнии
Морозные узоры на оконных стёклах
Кристаллы
Слайд 8
Обладает сложной структурой при любом увеличении;
Является (приближенно) самоподобной;
Обладает дробной метрической
размерностью, которая больше топологической;
Может быть построена рекурсивными процедурами
Свойства фракталов
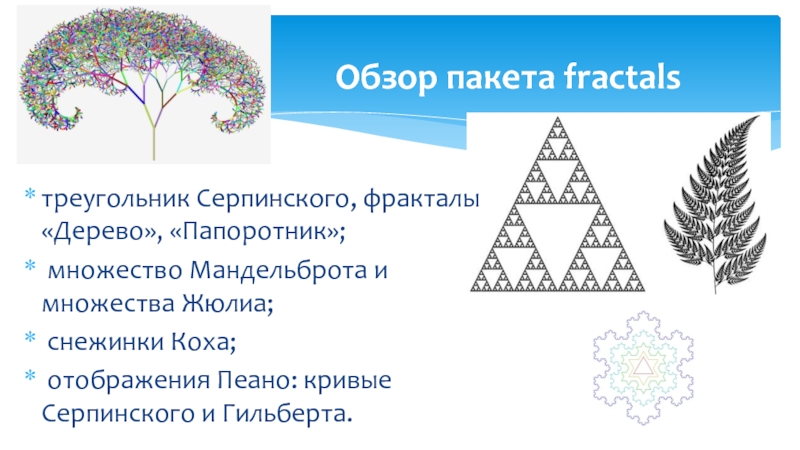
Слайд 9треугольник Серпинского, фракталы «Дерево», «Папоротник»;
множество Мандельброта и множества
Жюлиа;
снежинки Коха;
отображения Пеано: кривые Серпинского и
Гильберта.Обзор пакета fractals
Слайд 16паутинная диаграмма;
бифуркационная диаграмма;
эволюция орбиты одно- и двумерного отображений;
«игра в
хаос»;
система итерированных функций, заданная аффинными преобразованиями;
множества Жюлиа, Мандельброта;
Обзор
пакета dynamics
