Основные понятия алгебры логики.

рассуждение, закон».
Логика является одной из дисциплин, образующих математический фундамент информатики.
В

вычислительной технике и автоматике используются логические схемы – устройства, которые преобразуют двоичные сигналы.
Анализ и проектирование логических схем опираются на законы алгебры логики.
Любой язык программирования содержит логические переменные и средства для описания и вычисления логических выражений.
Логические методы применяются и при работе с базами данных.

изучает абстрактное мышление как средство познания объективного мира.

в странах Дальнего Востока (Китай, Индия), но в основе современной

логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель (384–322 гг. до н.э.), который впервые отделил логические формы речи от ее содержания.

(1646 – 1716) попытался построить первые логические исчисления, усовершенствовал и

уточнил логические символы.

На фундаменте, заложенном Лейбницем, другой великий математик, англичанин Джордж Буль (1815-1864) воздвиг здание новой области науки – математической логики.
Начальный раздел математической логики называют алгеброй логики или Булевой алгеброй.

в которой не рассматривается конкретное содержание основного понятия логики –

высказывания, а важно только истинно оно или ложно.

Основным объектом в логике является высказывание.

Высказывание – это повествовательное предложение,
о котором можно сказать истинно оно или ложно.

Высказывание называется
простым,
если никакая его часть сама
не является высказыванием.

Высказывание называется составным,
если оно состоит из простых высказываний,
соединенных логическими связками:
И, ИЛИ, частицей НЕ

«Сумма внутренних углов треугольника равна 1800»
Рассуждение – цепочка высказываний или

утверждений, определенным образом связанных друг с другом.
Например: «Если хотите начать работать на компьютере, то необходимо сначала включить электропитание»

Умозаключение – логическая операция, в результате которой из одного или нескольких данных высказываний получается (выводится) новое высказывание.
Например: «Все металлы электропроводны». «Ртуть является металлом». Путем умозаключения можно сделать вывод, что «Ртуть электропроводна».

Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты).
Например: (А ۸ (В ۷ С))

Z и называют
логическими переменными
Значения высказываний
ИСТИНА или ЛОЖЬ обозначают
соответственно цифрами

1 и 0
и называют логическими величинами

Составные высказывания называются
логическими выражениями и включают
в себя логические переменные,
операции логики и скобки для изменения
порядка действий операций

3»
C = «7 ≠ 3»
D = «B ۸ C» =

«(7 = 3) ۸ (7 ≠ 3)»

На языке алгебры логики эти высказывания можно записать так:
A = ИСТИНА = 1
B = ЛОЖЬ = 0
C = ИСТИНА = 1
D = ЛОЖЬ = 0

высказывания (элементарные)
Составные высказывания строятся из простых с помощью логических связок

(операций) "и", "или", "не"...

A и B
A и не B
не A или B

Это утро ясное и тёплое.
Это утро ясное и оно не тёплое.
Это утро не ясное или оно тёплое.

Любое высказывание либо ложно (0) либо истинно (1)

А и B одновременно истинны.
Операция И (логическое умножение, конъюнкция)

+ 3 = 5
7 – простое число и 9 –

простое число
2 * 2 = 5 и 2 * 2 ≥ 3
Книга – источник информации и 5 не больше 8

Ответ: истинными высказываниями являются: 1, 4

А и B одновременно ложны
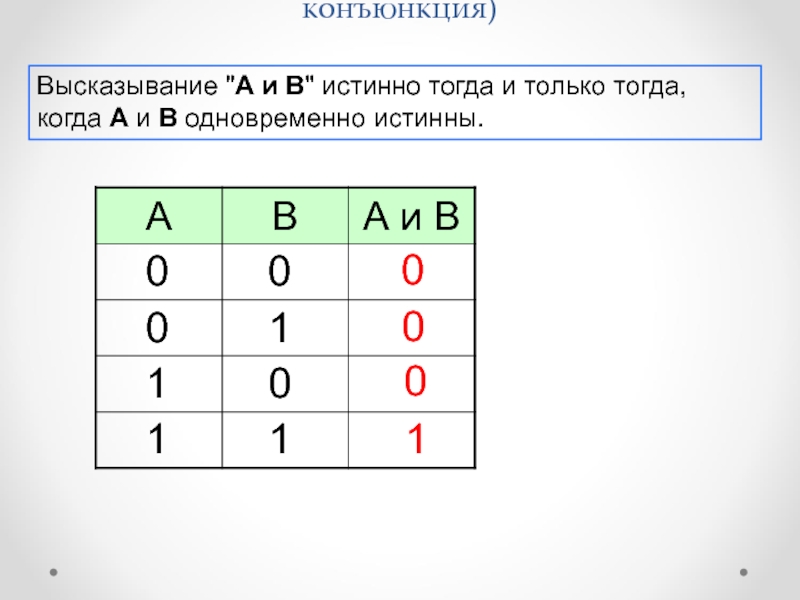
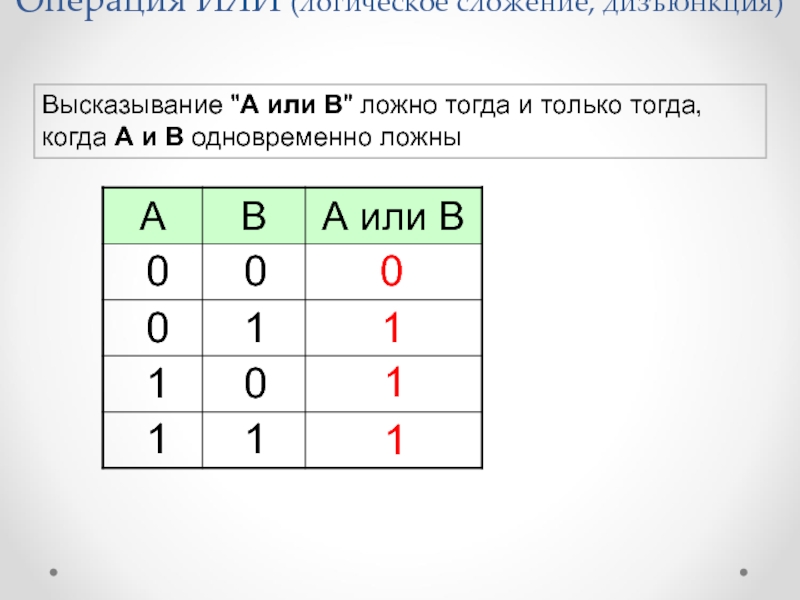
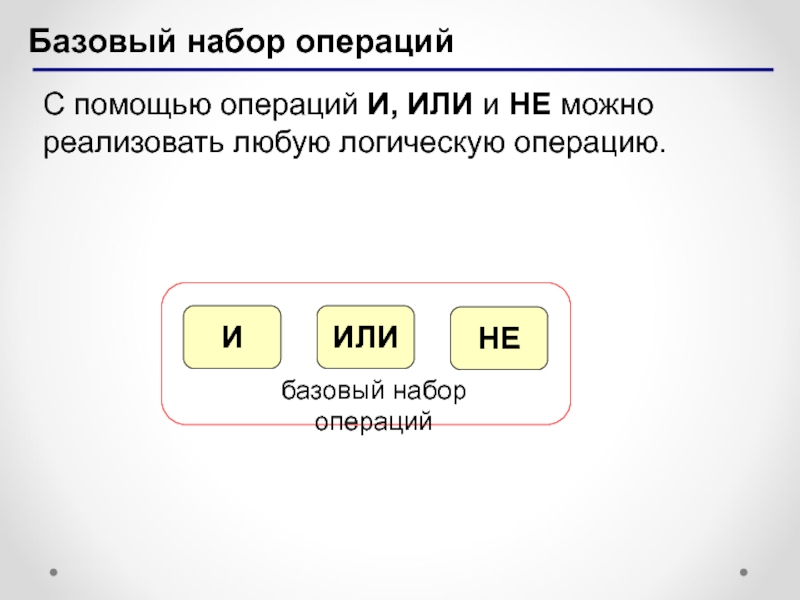
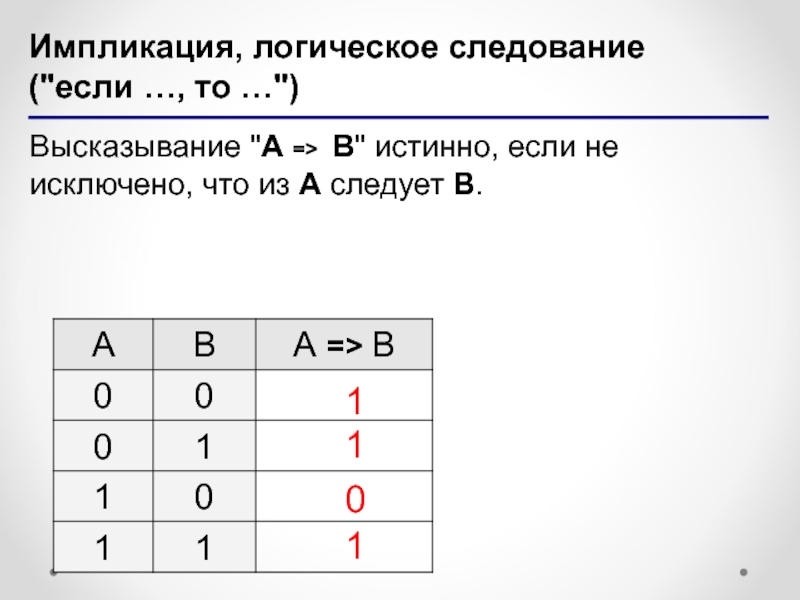Операция ИЛИ (логическое сложение, дизъюнкция)

– простое число
2 < 2 или 2 > 5
Луна

– спутник Марса или Луна – спутник Земли
Microsoft Word – текстовый редактор или Paint – графический редактор

Ответ: истинными высказываниями являются: 1, 3, 4

(инверсия, отрицание)

впадает в Каспийское море.
Число 28 не делится на число 7.
6

> 3.
4 ≤ 5.

реализовать любую логическую операцию.

то …")
Высказывание "A => B" истинно, если не исключено, что

из А следует B.

1

1

1

0

6, то 12 делится на 3.
Если 11 делится на 6,

то 11 делится на 3.
Если 15 делится на 10, то 15 делится на 2.
Если 15 делится на 3, то 15 делится на 6.

Ответ: истинными высказываниями являются: 1, 2, 3

истинно тогда и только тогда, когда А и B равны.

только тогда, когда 12 делится на 3.
11 делится на 6

тогда и только тогда, когда 11 делится на 3.
15 делится на 6 тогда и только тогда, когда 15 делится на 3.
15 делится на 5 тогда и только тогда, когда 15 делится на 4.

Ответ: истинными высказываниями являются: 1, 2

>, ≤, ≥, =, ≠)

Петя поедет в деревню и, если будет хорошая погода, то

он пойдет на рыбалку».
Проанализируем составное высказывание.
оно состоит из следующих простых высказываний: «Петя поедет в деревню», «Будет хорошая погода», «Он пойдет на рыбалку», обозначим их через логические переменные:
А= «Петя поедет в деревню»;
В = «Будет хорошая погода»;
С = «Он пойдет на рыбалку».
Запишем высказывание в виде логического выражения, учитывая порядок действий. Если необходимо, расставим скобки: F=A& (B→C).

В - «Волк травоядное животное».
Составьте из них все возможные составные

высказывания и определите их истинность.

Решение:

ЛОЖЬ (0)

ЛОЖЬ (0)

ИСТИНА (1)

ЛОЖЬ (0)

ИСТИНА (1)

ЛОЖЬ (0)

А↔В

А→В

¬ В

¬ А

А v В

А&В

= 1

= 0

двузначное.
А&В
Неверно, что корова хищное животное.
¬ А
На

уроке информатики ученики выполняли практическую работу и сообщали результаты учителю.
А&В
Если число делится на 2, то оно четное.
А => В
Если Маша сестра Саши, то Саша – брат Маши.
А => В
Водительские права можно получать тогда и только тогда, когда тебе исполнится 18 лет.
А↔В
На компьютере можно выполнить вычисления или набрать текст.
А v В

логических выражений:
F=(0v0)v(1v1)

2. F=(1v1)v(1v0)

3. F=(0&0)&(1&1)

4. F= (1v1)v(¬0&1)

(ответ: 1)

(ответ: 1)

(ответ: 0)

(ответ: 1)

1

0

1

1

1

1

1

1

1

0

0

1

1