Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия алгебры логики
Содержание
- 1. Основные понятия алгебры логики
- 2. Обработка любой информации на компьютере связана с выполнением процессором различных арифметических и логических операций.
- 3. Арифметические операцииСложение;Вычитание;Умножение;Деление.Логические операцииЛогическое сложение;Логическое умножение;Отрицание.Используются при проверке соотношений между различными величинами.
- 4. Алгебра логики или булева алгебраВ XIX веке
- 5. Основные понятия Алгебра – это раздел математики,
- 6. Основные понятия Логика - это наука
- 7. Основные понятия Алгебра логики –
- 8. НАПРИМЕР:«6 - четное число» - это высказывание,
- 9. Например предложения «ученик девятого класса» не является
- 10. Предложения, не являющиеся высказываниями
- 11. Слайд 11
- 12. Слайд 12
- 13. Основные логические операциилогическое отрицание (инверсия);логическое умножение (конъюнкция);логическое сложение (дизъюнкция);логическое следование (импликация);логическое равенство (эквивалентность).
- 14. ИНВЕРСИЯОбозначение:не A, ¬ A, ĀПример:А - Дождя
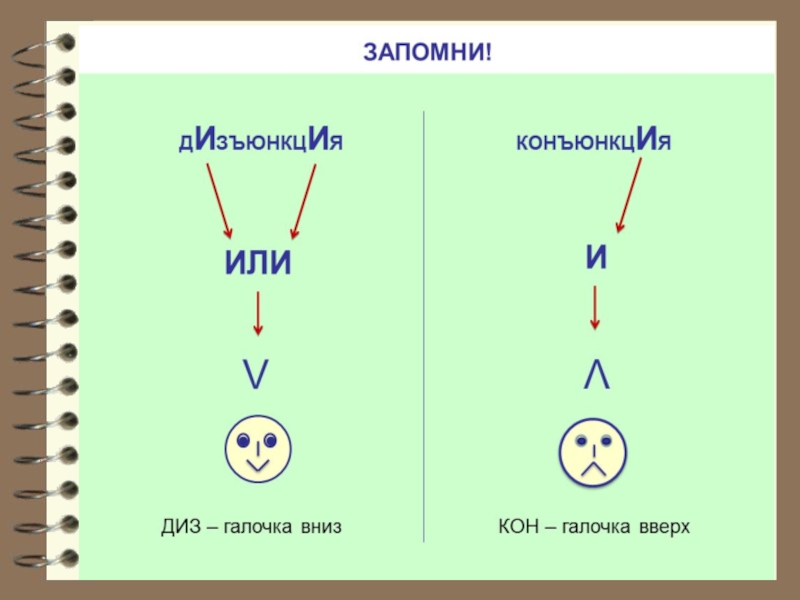
- 15. КОНЪЮНКЦИЯОбозначения: и, ^, &, ∙Пример:А - Дождя
- 16. ДИЗЪЮНКЦИЯОбозначения: или, v, +Пример:А - Дождя не
- 17. Слайд 17
- 18. ИМПЛИКАЦИЯОбозначения: если, … то; →; ⇒Пример:А -
- 19. ЭКВИВАЛЕНТНОСТЬОбозначения: ↔« тогда и только тогда, когда».Пример:А
- 20. Скачать презентанцию
Обработка любой информации на компьютере связана с выполнением процессором различных арифметических и логических операций.
Слайды и текст этой презентации
Слайд 2Обработка любой информации на компьютере связана с выполнением процессором различных
арифметических и логических операций.
Слайд 3Арифметические операции
Сложение;
Вычитание;
Умножение;
Деление.
Логические операции
Логическое сложение;
Логическое умножение;
Отрицание.
Используются при проверке соотношений между различными
величинами.
Слайд 4Алгебра логики или булева алгебра
В XIX веке английский математик и
логик Джордж Буль разработал её основные положения.
«Логика» от древнегреческого logos,
означающего «слово, мысль, понятие, рассуждение, закон»Слайд 5Основные понятия
Алгебра – это раздел математики, предназначенный для описания действий
над переменными величинами, которые принято обозначать строчными латинскими буквами, например
a, b, x, y и т.д.Слайд 6Основные понятия
Логика - это наука о законах и операциях
правильного мышления.
Логика высказываний - определенная совокупность формул.
Слайд 7Основные понятия
Алгебра логики – аппарат, который позволяет выполнять
действия над высказываниями.
Высказывание - всякое предложение, которое
может быть истинным или ложным.Истинное высказывание обозначается - 1, ложное - 0
Слайд 8НАПРИМЕР:
«6 - четное число» - это высказывание, т.к. оно истинное.
«Подснежники
зацветают в сентябре» - это тоже высказывание т.к. оно ложное.
Но
не всякое предложение является высказыванием. Слайд 9
Например
предложения «ученик девятого класса»
не является высказыванием.
Предложение ничего не
утверждает об ученике.
Вопросительные и восклицательные предложения также не являются высказываниями,
поскольку говорить об их истинности или ложности не имеет смысла.Слайд 13Основные логические операции
логическое отрицание (инверсия);
логическое умножение (конъюнкция);
логическое сложение (дизъюнкция);
логическое следование
(импликация);
логическое равенство (эквивалентность).
Слайд 14ИНВЕРСИЯ
Обозначение:не A, ¬ A, Ā
Пример:
А - Дождя не будет
Ā -
Неверно, что дождя не будет
Таблица истинности
Логическое отрицание
1) НЕ
2) НЕВЕРНО, ЧТО
Слайд 15КОНЪЮНКЦИЯ
Обозначения: и, ^, &, ∙
Пример:
А - Дождя не будет.
В -
Небо голубое.
А ^ В - Дождя не будет и небо
голубое.Таблица истинности:
Логическое умножение
И
Слайд 16ДИЗЪЮНКЦИЯ
Обозначения: или, v, +
Пример:
А - Дождя не будет.
В - Небо
голубое.
А V В - Дождя не будет или небо голубое.
Таблица
истинности:Логическое сложение
ИЛИ
Слайд 18ИМПЛИКАЦИЯ
Обозначения: если, … то; →; ⇒
Пример:
А - Дождя не будет.
В
- Небо голубое.
А → В - Если дождя не будет,
то небо голубое.Таблица истинности:
Условная связь
ЕСЛИ, ТО
Слайд 19ЭКВИВАЛЕНТНОСТЬ
Обозначения: ↔
« тогда и только тогда, когда».
Пример:
А - Дождя не
будет.
В - Небо голубое.
А↔В - Дождя не будет тогда и
только тогда, когда небо голубое.Таблица истинности:
Если и только если
2) Тогда и только тогда, когда