Слайд 1Основы логики и логические основы компьютера
Слайд 2Логика – это наука о формах и способах мышления.
Законы логики
отражают в сознании человека свойства, связи и отношения объектов окружающего
мира. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.
Алгебра логики – это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания.
Слайд 3Свое понимание окружающего мира человек формулирует в форме высказываний.
Высказывание –
это форма мышления, в которой что-либо утверждается или отрицается о
свойствах реальных предметов и отношениях между ними.
Слайд 4
Высказывание – повествовательное предложение, о котором можно сказать, истинно оно
или ложно.
Высказывание может принимать только одно из двух логических значений
– истинно (1) или ложно (0).
Истинным будет высказывание, в котором правильно отражаются свойства и отношения реальных вещей.
Ложным высказывание будет в том случае, если оно не соответствует реальной действительности.
Слайд 5Примеры высказываний:
Земля – планета Солнечной системы.
3+6=10
Почему следующие предложения не являются
высказываниями:
Уходя, гасите свет.
Какого цвета этот дом?
Посмотрите в окно.
Слайд 6Высказывания бывают простые и сложные.
Простое высказывание (логическая переменная) содержит только
одну простую мысль.
Логические переменные обычно обозначают буквами латинского алфавита:
A, B, C …
Например, А={Квадрат – это ромб}
Слайд 7Сложное высказывание (логическая функция) содержит несколько простых мыслей, соединенных между
собой с помощью логических операций.
Например,
F(A,B)={Лил дождь, и дул холодный ветер}
F(A,B)={Процессор
является устройством обработки информации и принтер является устройством печати.
А
В
Слайд 8Если истинность или ложность простых высказываний устанавливается в результате соглашения
на основании здравого смысла, то истинность или ложность составных высказываний
вычисляется с помощью использования алгебры логики.
Слайд 9Алгебра логики
Алгебра логики была разработана для того, чтобы можно было
определять истинность или ложность сложных (составных) высказываний, не вникая в
их содержание.
В алгебре логики над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания.
Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Слайд 10Значение логической функции можно определить с помощью специальной таблицы (таблицы
истинности)
Таблица истинности – таблица, в которой перечислены все возможные значения
входящих логических переменных и соответствующие им значения функции.
Слайд 11Основные логические операции:
Отрицание (инверсия), от латинского inversio – переворачиваю:
соответствует частице
НЕ, словосочетанию НЕВЕРНО, ЧТО;
обозначение: не А, Ᾱ, ¬А;
таблица истинности:
Слайд 12Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное
высказывание истинным.
А={25+25=50}
Ᾱ={Неверно, что 25+25=50}
- А={25+25=51}
Ᾱ={Неверно, что
25+25=51}
Слайд 13Логическое сложение (дизъюнкция), от латинского disjunctio – различаю:
соответствует союзу ИЛИ;
обозначение:
+, или, v;
таблица истинности:
Слайд 14Составное высказывание, образованное в результате операции логического сложения (дизъюнкции) ложно
тогда и только тогда, когда ложны все входящие в него
простые высказывания.
F={2+2=4 или 3+3=7};
F={2+2=5 или 3+3=6};
F={2+2=4 или 3+3=6};
F={2+2=5 или 3+3=7};
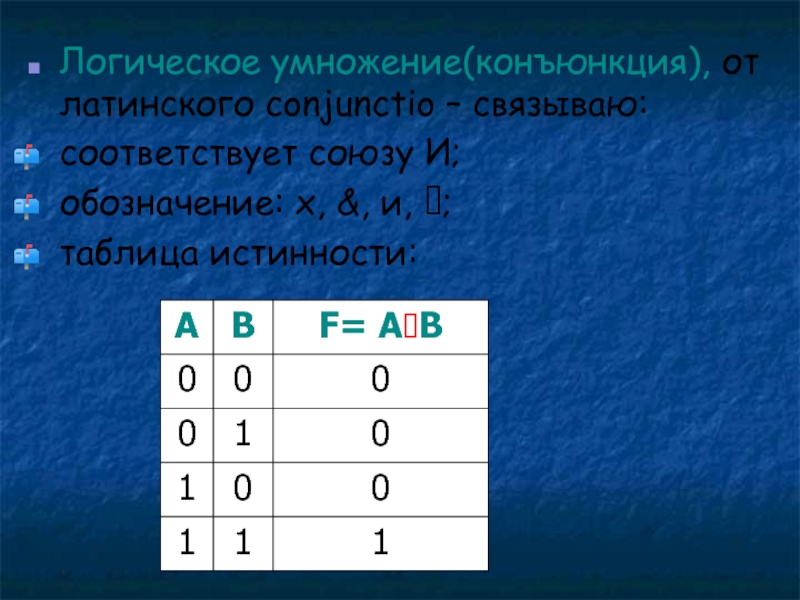
Слайд 15Логическое умножение(конъюнкция), от латинского conjunctio – связываю:
соответствует союзу И;
обозначение: х,
&, и, ;
таблица истинности:
Слайд 16Составное высказывание, образованное в результате операции логического умножения (конъюнкции) истинно
тогда и только тогда, когда истинны все входящие в него
простые высказывания.
- F={2+2=5 и 3+3=6};
F={2+2=4 и 3+3=7};
F={2+2=5 и 3+3=7};
F={2+2=4 и 3+3=6};
Слайд 17Даны два высказывания:
А={Число 5 - простое}
В={Число 4 - нечетное}
Очевидно, что
А=1, В=0. В чем заключаются высказывания:
а) Ᾱ
б) ¬В
в) А۸В
г)
АvВ
Какие из этих высказываний истинны?
={Число 5 – не простое}
={Число 4 - четное}
={Число 5 – простое и число 4 - нечетное}
={Число 5 – простое или число 4
нечетное}
Слайд 18По мишеням произведено три выстрела. Рассмотрим высказывание: Рk={мишень поражена k-м
выстрелом}, где k=1, 2, 3.
Что означают следующие высказывания:
а) Р1v Р2
v Р3
б) Р1 Р2 Р3
в)
Мишень поражена первым
выстрелом или вторым выстрелом или третьим выстрелом.
Мишень поражена и первым
выстрелом, и вторым выстрелом, и третьим выстрелом.
Неверно, что мишень поражена
первым выстрелом или вторым
выстрелом или третьим выстрелом.
Слайд 19Логические выражения и таблицы истинности.
Составные высказывания можно представить в виде
логического выражения или формулы, которая состоит из логических переменных, обозначающих
высказывания, и знаков логических операций.
Логические операции выполняются в следующем порядке: инверсия, конъюнкция, дизъюнкция. Скобки позволяют этот порядок изменить:
Слайд 20Для записи составного высказывания в виде логического выражения на формальном
языке (языке алгебры логики) в составном высказывании нужно выделить простые
высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание
(2•2=5 или 2•2=4) и (2•2≠5 или 2•2≠4) и проанализируем полученное составное высказывание. Оно содержит два простых высказывания:
А={2•2=5} – ложно (0)
В={2•2=4} – истинно (1)
Тогда составное высказывание можно записать в следующем виде: (А∨В)∧(¬А∨¬В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры логики, не обращаясь к смысловому содержанию высказываний.
Подставив в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (А∨В)∧(¬А∨¬В) =(0∨1)∧(1∨0) = 1∧1 = 1.
Слайд 21Значение логической функции можно определить с помощью специальной таблицы (таблицы
истинности)
Таблица истинности – таблица, в которой перечислены все возможные значения
входящих логических переменных и соответствующие им значения функции.
Слайд 22Построение таблиц истинности:
Определить число переменных;
Определить число строк в таблице истинности;
Записать
все возможные значения переменных;
Определить количество логических операций и их порядок;
Записать
логические операции в таблицу истинности и определить для каждой их значение.
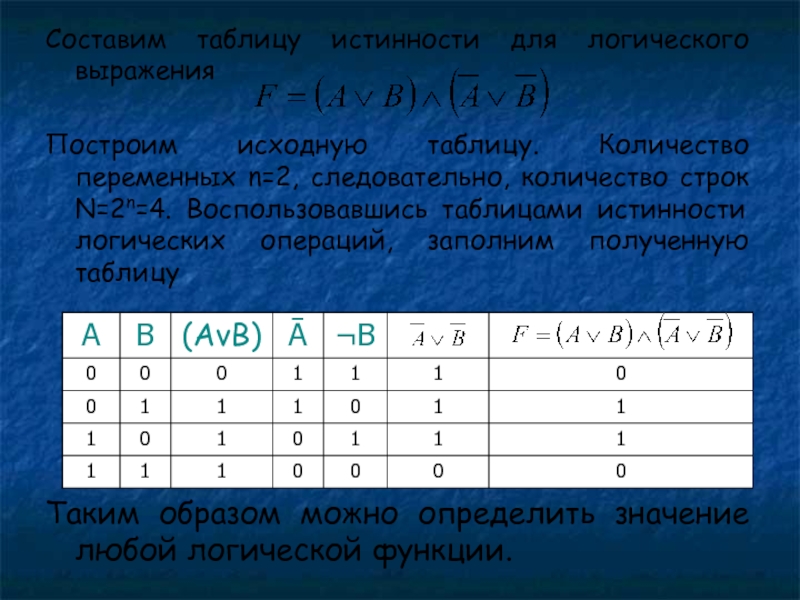
Слайд 23Составим таблицу истинности для логического выражения
Построим исходную таблицу. Количество переменных
n=2, следовательно, количество строк N=2n=4. Воспользовавшись таблицами истинности логических операций,
заполним полученную таблицу
Таким образом можно определить значение любой логической функции.
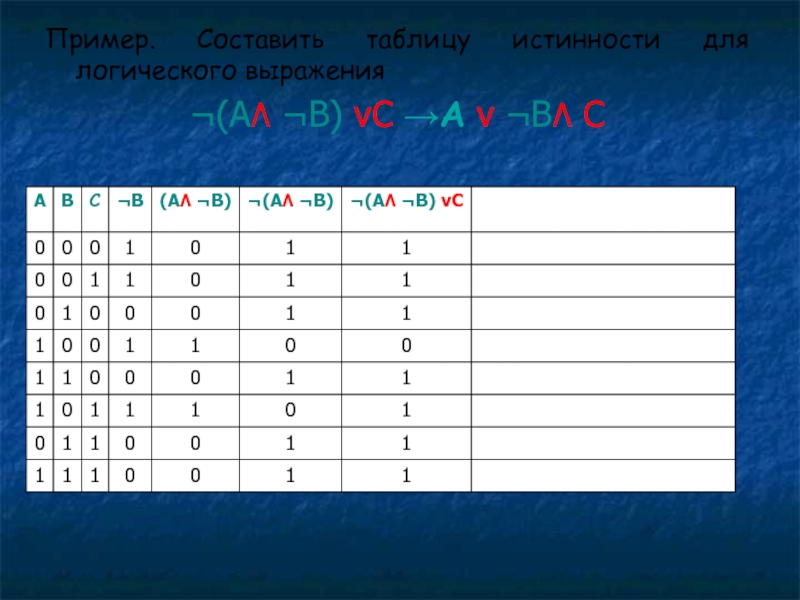
Слайд 24Пример. Составить таблицу истинности для логического выражения
¬(А۸ ¬В) vС →А
v ¬В۸ С
Слайд 25Символом F обозначено одно из указанных ниже логических выражений от
трех аргументов: Х, У, Z.
Дан фрагмент истинности выражения F:
Какое выражение
соответствует F ?
1) ¬Х ۸ ¬У ۸ Z
2) Х ۸ У ۸ ¬Z
3) Х v ¬У v ¬Z
4) ¬Х v ¬У v Z
Слайд 26Символом F обозначено одно из указанных ниже логических выражений от
трех аргументов: Х, У, Z.
Дан фрагмент истинности выражения F:
Какое выражение
соответствует F ?
1) ¬Х ۸ У ۸ Z
3) Х ۸ ¬У ۸ ¬Z
2) ¬Х v У v ¬Z
4) ¬Х v ¬У v Z
Слайд 27Другие логические операции
Импликация (логическое следование), от латинского implicatio – тесно
связываю:
соответствует речевому обороту ЕСЛИ … ТО
обозначение: →, ⇒;
таблица истинности:
Слайд 28Составное высказывание, образованное с помощью операции логического следования (импликации), ложно
тогда и только тогда, когда из истинной предпосылки (первого высказывания)
следует ложный вывод (второе высказывание)
Например, высказывание «Если число делится на 10, то оно делится на 5» истинно, так как истинны и первое высказывание, и второе высказывание.
Высказывание «Если число делится на 10, то оно делится на 3» ложно, так как из истинной предпосылки делается ложный вывод.
Слайд 29Эквивалентность (логическое равенство), от латинского aequivalens – равноценное:
соответствует речевому обороту
ЭКВИВАЛЕНТНО
обозначение: =, ↔, ⇔;
таблица истинности:
Слайд 30Составное высказывание, образованное с помощью логической операции эквивалентности, истинно тогда
и только тогда, когда оба высказывания одновременно либо ложны, либо
истинны.
Рассмотрим два высказывания: А={Компьютер может производить вычисления} и В={Компьютер включен}. Составное высказывание, полученное с помощью операции эквивалентности, истинно, когда оба высказывания либо истинны, либо ложны:
{Компьютер может производить вычисления тогда и только тогда, когда компьютер включен}.
{Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен}.
Слайд 31Составное высказывание, полученное с помощью операции эквивалентности, ложно, когда одно
высказывание истинно, а другое ложно:
{Компьютер может производить вычисления тогда и
только тогда, когда компьютер не включен}.
{Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен}.
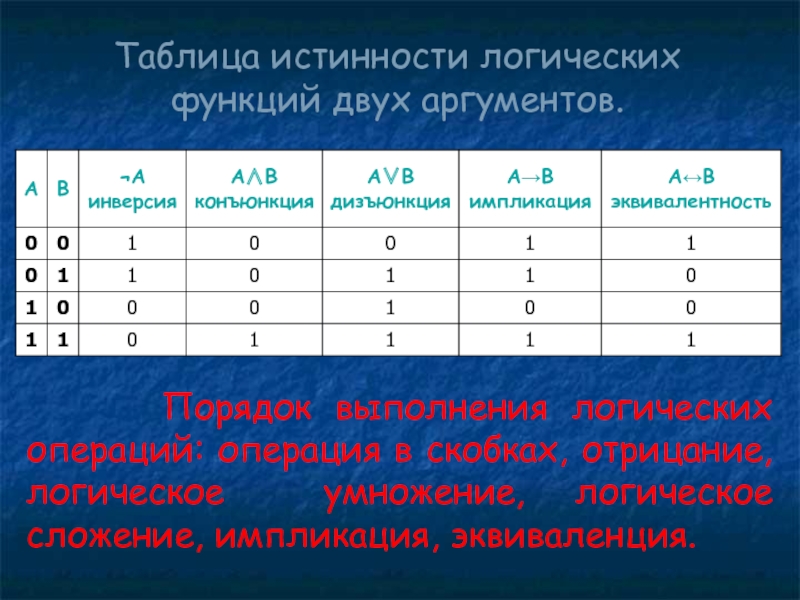
Слайд 32Таблица истинности логических функций двух аргументов.
Порядок выполнения
логических операций: операция в скобках, отрицание, логическое умножение, логическое сложение,
импликация, эквиваленция.
Слайд 33Доказать, используя таблицы истинности, что операция эквивалентности А⇔В равносильна логическому
выражению: (А∨¬В)∧(¬А∨В).
Доказать, используя таблицы истинности, что
.
Доказать, используя таблицы истинности, что .
Слайд 34Решение задач
Для какого имени истинно высказывание
¬(Первая буква имени гласная→Четвертая
буква имени согласная) :
1) ЕЛЕНА 2) ВАДИМ 3)
АНТОН 4) ФЕДОР
Решение:
Поскольку данное высказывание истинно, его отрицание (Первая буква имени гласная →Четвертая буква имени согласная) ложно.
Это высказывание является импликацией и ложно только в том случае, когда левая часть его (Первая буква имени гласная) истинна, а правая (Четвертая буква имени согласная) – ложна. То есть , первая и четвертая буквы имени – гласные.
Этому условию удовлетворяет только имя АНТОН.
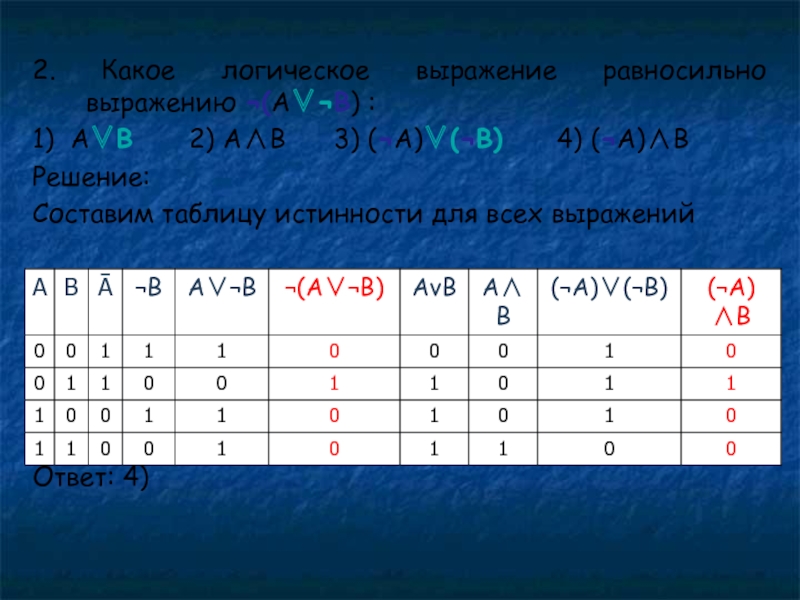
Слайд 352. Какое логическое выражение равносильно выражению ¬(А∨¬В) :
1) А∨В
2) А∧В 3) (¬А)∨(¬В)
4) (¬А)∧В
Решение:
Составим таблицу истинности для всех выражений
Ответ: 4)
Слайд 363. Для какого из указанных значений числа Х истинно высказывание
(Х>4) ∨((X>1)→(X>4)) :
1) 1 2) 2
3) 3 4) 4
Решение:
Подставим последовательно варианты ответов в исходное выражение и вычислим его значение
(1>4) ∨((1>1)→(1>4)) =0∨(0→0)=0∨1=1
(2>4) ∨((2>1)→(2>4)) =0∨(1→0)=0∨0=0
(3>4) ∨((3>1)→(3>4)) =0∨(1→0)=0∨0=0
(4>4) ∨((4>1)→(4>4)) =0∨(1→0)=0∨0=0
Ответ: 1)
Слайд 37Логические законы и правила преобразования логических выражений
Законы логики отражают наиболее
важные закономерности логического мышления. В алгебре логики законы логики записываются
в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.
Закон тождества. Всякое высказывание тождественно самому себе: А=А
Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А истинно, то его отрицание должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно: А∧(¬А)=0
Слайд 38Закон исключения третьего. Высказывание может быть либо истинным, либо ложным.
Это означает, что результат логического сложения высказывания и его отрицания
всегда принимает значение «истина»: А∨(¬А)=1
Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание: ¬ (¬А)=А
Законы де Моргана.
Слайд 39Закон коммутативности. В обычной алгебре слагаемые и множители можно менять
местами. В алгебре логики можно менять местами логические переменные при
операциях логического умножения и логического сложения:
А∧В = В∧А
А∨В = В∨А
Закон ассоциативности. Если в логическом выражении используются только операции логического умножения или только логического сложения, то можно пренебрегать скобками или произвольно их расставлять:
(А∧В) ∧С=А∧(В∧С)
(А∨В) ∨С=А∨(В∨С)
Слайд 40Закон дистрибутивности. В отличии от обычной алгебры, где за скобки
можно выносить только общие множители, в алгебре логики можно выносить
за скобки как общие множители, так и общие слагаемые:
(А∧В) ∨(А∧С) = А∧(В∨С)
(А∨В) ∧(А∨С )= А∨(В∧С)
Полезно также знать формулу для выражения импликации через отрицание и логическое сложение А→В=¬А∨В
Пример. Упростить логическое выражение:
(А∧В) ∨(А∧¬В)
Воспользуемся законом дистрибутивности и вынесем за скобки А: А∧(В∨¬В).
По закону исключения третьего (В∨¬В)=1, следовательно: А∧(В∨¬В)=А∧1=А
Слайд 411. Упростить логические выражения:
а) (А∨¬А) ∧В
Решение:
(А∨¬А) ∧В = 1∧В = В
б) А∧(А∨В)∧(В∨¬В)
Решение:
А∧(А∨В)∧(В∧¬В) = А∧(А∨В)∧0 = 0
Слайд 421. Для какого символьного выражения неверно:
Первая буква гласная →¬(Третья буква
согласная)?
1) abedc 2) becde
3) babas 4) abcab
2. Для какого имени истинно высказывание:
¬(Первая буква имени согласная → Третья буква имени гласная)?
1) Юлия 2) Петр 3) Алексей 4) Ксения
3. Для какого из значений числа У высказывание
(У<5) ∧ ((Y>1) →(Y>5)) будет истинным?
1) 1 2) 2 3) 3 4) 4
Решить следующие логические задачи:
Слайд 434. Для какого символьного выражения верно:
¬(Первая буква согласная) ∧ ¬(Вторая
буква гласная)?
1) abcde 2) bcade
3) babas 4) cabab
5. Какое из приведенных названий животных удовлетворяет логическому условию
В слове пять букв ∧ Четвертая буква гласная?
1) Зебра 2) Слон 3) Кабан 4) Олень
6. Для какого из значений числа У высказывание
((У<2) ∨ (Y>4)) →(Y>3) будет ложным?
1) 1 2) 2 3) 3 4) 4
Слайд 447. Для какого из названий животных ложно высказывание:
Четвертая буква гласная
→ ¬(Вторая буква согласная)?
1) Собака 2)
Жираф 3) Верблюд 4) Страус
8. Для какого имени ложно высказывание:
Первая буква гласная ∨ Четвертая буква согласная?
1) Петр 2) Алексей 3) Наталья 4) Елена
9. Какое из приведенных имен удовлетворяет логическому условию
Первая буква гласная ∧Четвертая буква согласная ∨В слове четыре буквы?
1) Сергей 2) Вадим 3) Антон 4) Илья