Основы логики(теория)

Содержание

1. Основы логики(теория)
2. ОпределениеЛогика – это наука о формах и способах мышленияФормы мышленияпонятиесуждение(высказывание, утверждение)умозаключение
3. ПонятиеПонятие – это форма мышления, фиксирующая основные,
4. ВысказываниеВысказывание – это форма мышления, в которой
5. Вопросительные и восклицательные предложения не являются высказываниями,
6. УмозаключениеУмозаключение – это форма мышления, с помощью
7. Алгебра высказыванийСлужит для определения истинности или ложности
8. Логические операцииЛогическое умножениеОбъединение двух (или нескольких) высказываний
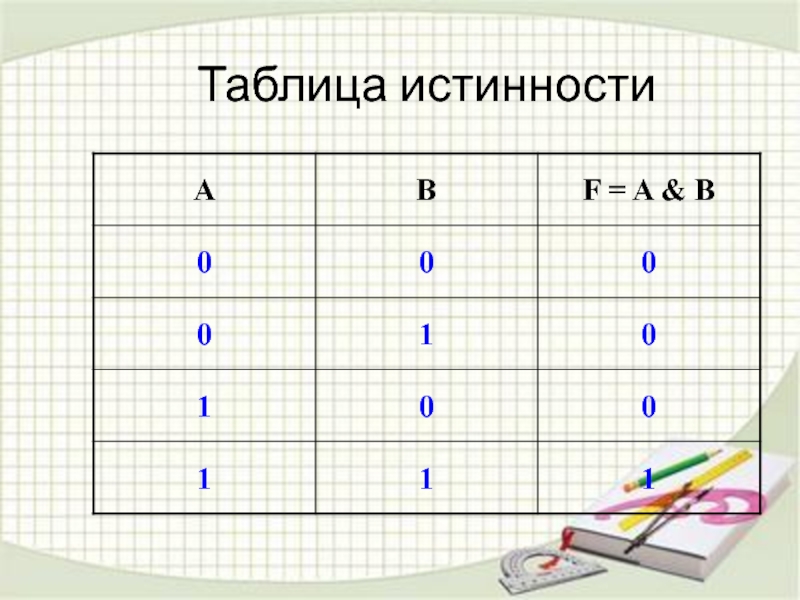
9. Обозначение операции логического умножения: &, ^, *;Пусть
10. Таблица истинности
11. Логическое сложениеОбъединение двух (или нескольких) высказываний в
12. Обозначение операции логического сложения: ; +;Пусть имеется
13. Таблица истинности
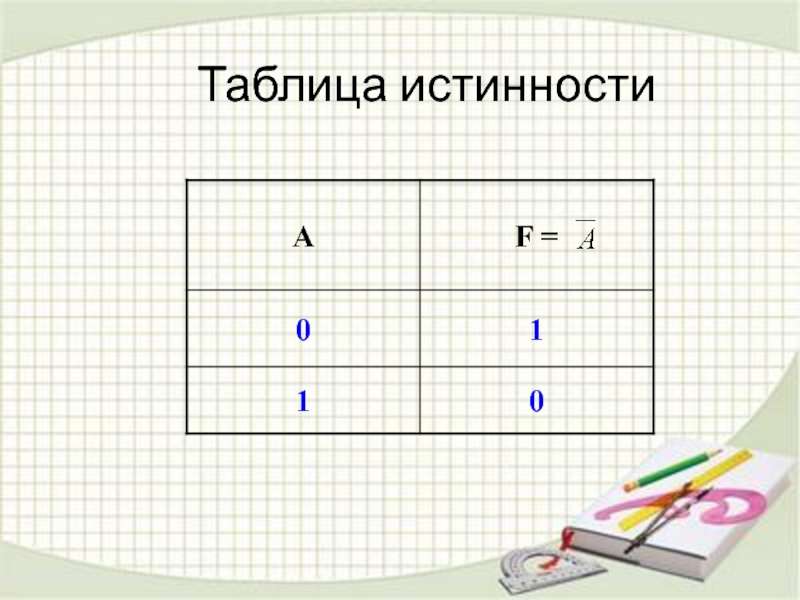
14. Логическое отрицаниеПрисоединение частицы «не» к высказыванию называется
15. Таблица истинности
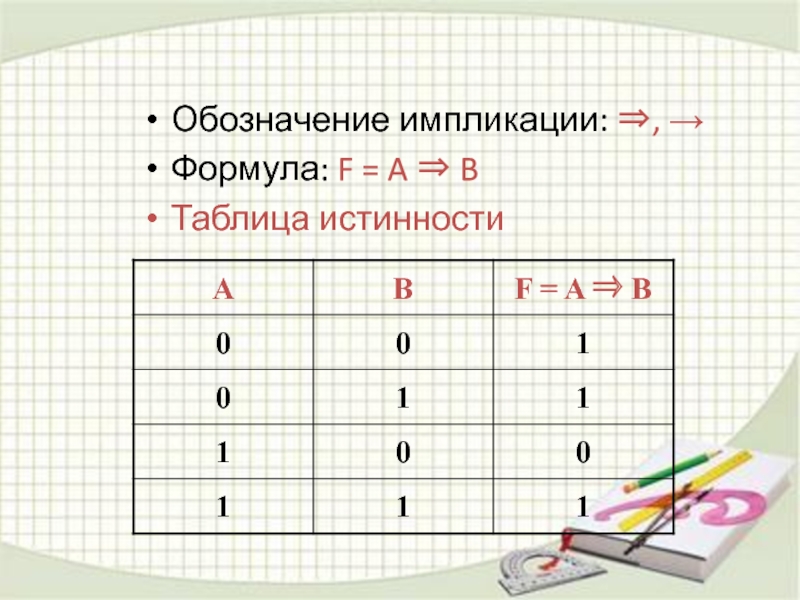
16. Логическое следованиеСоединение двух высказываний в одно с
17. Обозначение импликации: ,  Формула: F = A  BТаблица истинности
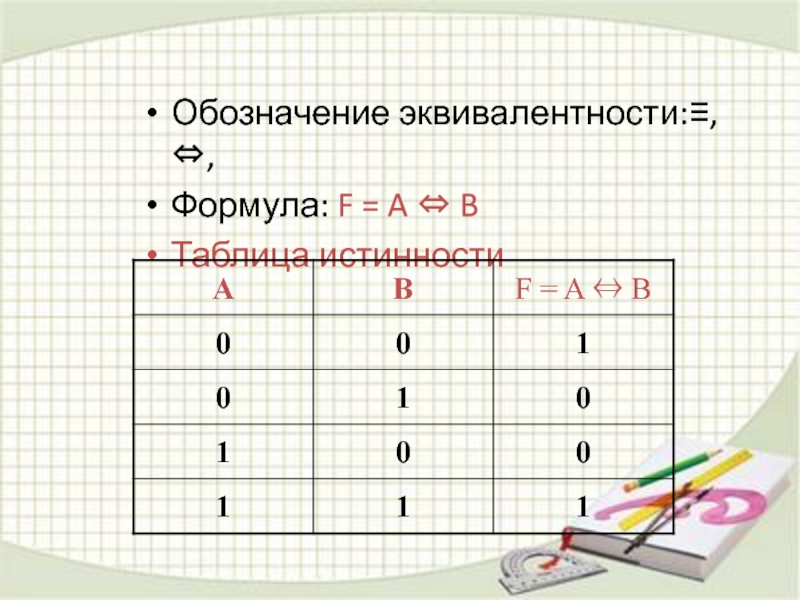
18. Логическое равенствоСоединение двух высказываний в одно помощью
19. Обозначение эквивалентности:, , Формула: F = A  BТаблица истинности
20. Приоритет действийИнверсияКонъюнкцияДизъюнкцияСоставление таблиц истинностиЧисло строк = 2n
21. Законы логикиЗакон тождества: всякое высказывание тождественно самому
22. Законы логикиЗакон двойного отрицания: если дважды отрицать
23. Законы логикиЗакон дистрибутивности:Законы Моргана:Поглощение 1:Поглощение 0:Поглощения:
24. Скачать презентанцию

ОпределениеЛогика – это наука о формах и способах мышленияФормы мышленияпонятиесуждение(высказывание, утверждение)умозаключение

Слайды и текст этой презентации

Слайд 1ОСНОВЫ ЛОГИКИ
Учитель информатики МБОУ «Великомихайловская СОШ Новооскольского района Белгородской области»

Ерошенко И.В.
ТЕОРИЯ

Слайд 2Определение
Логика – это наука о формах и способах мышления
Формы мышления
понятие
суждение
(высказывание,

утверждение)
умозаключение

Слайд 3Понятие
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта;
Понятие

имеет две стороны: содержание и объем;
Содержание – это совокупность существенных

признаков объекта;
Объем – это совокупность предметов, на которые распространяется понятие;

ПонятиеПонятие – это форма мышления, фиксирующая основные, существенные признаки объекта;Понятие имеет две стороны: содержание и объем;Содержание –

Слайд 4Высказывание
Высказывание – это форма мышления, в которой что-либо утверждается или

отрицается о реальных предметах, их свойствах и отношениях между ними;
Высказывание

может быть либо истинно, либо ложно;
Высказывания могут быть выражены с помощью естественных и формальных языков;
Высказывания могут быть выражены только повествовательным предложением;
Высказывания могут быть простыми и составными;
Истинность простых высказываний определяется на основании здравого смысла;
Истинность составных высказываний определяется с помощью алгебры высказываний.
Пример: Зимой идет снег. Процессор является устройством обработки информации

ВысказываниеВысказывание – это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и

Слайд 5
Вопросительные и восклицательные предложения не являются высказываниями,
т.к. в них

ничего не утверждается и не отрицается

Например:
Нельзя касаться оголенных проводов!
Когда закончится

урок?
Какого цвета этот стол?
Нельзя пить и есть в кабинете Информатики
и ИКТ!

Вопросительные и восклицательные предложения не являются высказываниями, т.к. в них ничего не утверждается и не отрицаетсяНапример:Нельзя касаться

Слайд 6Умозаключение
Умозаключение – это форма мышления, с помощью которой из одного

или нескольких высказываний может быть получено новое суждение;
Посылками умозаключения могут

быть только истинные суждения
Все металлы - простые вещества. Литий - металл.→ Литий - простое вещество.

Один из углов треугольника равен 90º. → Этот треугольник прямоугольный.

УмозаключениеУмозаключение – это форма мышления, с помощью которой из одного или нескольких высказываний может быть получено новое

Слайд 7Алгебра высказываний
Служит для определения истинности или ложности составных высказываний, не

вникая в их содержание;
В алгебре высказываний простым высказываниям ставятся в

соответствие логические переменные, обозначаемые латинскими буквами:
Например: A – «Крокодилы летают»
B – «Земля вращается вокруг Солнца»
Если высказывание истинно, то ему соответствует значение логической переменной 1, если ложно – 0;
Тогда: A = 0, B = 1
Над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания;

Алгебра высказыванийСлужит для определения истинности или ложности составных высказываний, не вникая в их содержание;В алгебре высказываний простым

Слайд 8Логические операции
Логическое умножение
Объединение двух (или нескольких) высказываний в одно с

помощью союза «и» («а», «но») называется операцией логического умножения или

конъюнкцией.
Правило истинности
Составное высказывание, образованное в результате логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны входящие в него простые высказывания.

Логические операцииЛогическое умножениеОбъединение двух (или нескольких) высказываний в одно с помощью союза «и» («а», «но») называется операцией

Слайд 9Обозначение операции логического умножения: &, ^, *;
Пусть имеется два простых

высказывания A и B, составим составное высказывание F с помощью

конъюнкции: F = A & B;
Значение логической функции можно определить с помощь таблицы истинности.

Обозначение операции логического умножения: &, ^, *;Пусть имеется два простых высказывания A и B, составим составное высказывание

Слайд 10Таблица истинности

Слайд 11Логическое сложение

Объединение двух (или нескольких) высказываний в одно с помощью

союза «или» называется операцией логического сложения или дизъюнкцией.
Правило истинности
Составное высказывание,

образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

Логическое сложениеОбъединение двух (или нескольких) высказываний в одно с помощью союза «или» называется операцией логического сложения или

Слайд 12Обозначение операции логического сложения: ; +;
Пусть имеется два простых высказывания

A и B, составим составное высказывание F с помощью дизъюнкции:

F = A  B;
Значение логической функции можно определить с помощь таблицы истинности.

Обозначение операции логического сложения: ; +;Пусть имеется два простых высказывания A и B, составим составное высказывание F

Слайд 13Таблица истинности

Слайд 14Логическое отрицание
Присоединение частицы «не» к высказыванию называется операцией логического отрицания

или инверсией
Правило истинности
Логическое отрицание (инверсия) делает истинное высказывание ложным, а

ложное - истинным.
Обозначение инверсии: ¬; ¯
Пусть имеется простое высказывание A, составим составное высказывание F с помощью инверсии: F = ¬ A (F = )

Логическое отрицаниеПрисоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсиейПравило истинностиЛогическое отрицание (инверсия) делает истинное

Слайд 15Таблица истинности

Слайд 16Логическое следование
Соединение двух высказываний в одно с помощью оборота речи

«если…, то…» называется операцией логического следования или импликацией
Правило истинности
Составное высказывание,

образованное с помощью операции логического следования (импликации), ложно тогда, когда из истинной посылки (высказывания) следует ложный вывод (второе высказывание)

Логическое следованиеСоединение двух высказываний в одно с помощью оборота речи «если…, то…» называется операцией логического следования или

Слайд 17Обозначение импликации: , 
Формула: F = A  B
Таблица

истинности

Слайд 18Логическое равенство
Соединение двух высказываний в одно помощью оборота речи «тогда

и только тогда, когда» называется операцией логического равенства или эквивалентностью
Правило

истинности
Составное высказывание, образованное с помощью операции логического равенства (эквивалентности), истинно только тогда, когда оба высказывания одновременно либо истинны, либо ложны

Логическое равенствоСоединение двух высказываний в одно помощью оборота речи «тогда и только тогда, когда» называется операцией логического

Слайд 19Обозначение эквивалентности:, ,
Формула: F = A  B
Таблица истинности

Слайд 20Приоритет действий
Инверсия
Конъюнкция
Дизъюнкция
Составление таблиц истинности
Число строк = 2n , где n

–число логических переменных;
Число столбцов = число логических переменных + число

логических операций

Приоритет действийИнверсияКонъюнкцияДизъюнкцияСоставление таблиц истинностиЧисло строк = 2n , где n –число логических переменных;Число столбцов = число логических

Слайд 21Законы логики
Закон тождества: всякое высказывание тождественно самому себе
Закон непротиворечия:

высказывание не может быть одновременно истинным и ложным
Закон исключения

третьего: высказывание может быть либо истинным, либо ложным третьего не дано

Законы логикиЗакон тождества: всякое высказывание тождественно самому себе Закон непротиворечия: высказывание не может быть одновременно истинным и

Слайд 22Законы логики
Закон двойного отрицания: если дважды отрицать одно и то

же высказывание, то в результате получится исходное высказывание
Закон коммутативности:

Закон

ассоциативности:

Законы логикиЗакон двойного отрицания: если дважды отрицать одно и то же высказывание, то в результате получится исходное

Слайд 23Законы логики
Закон дистрибутивности:

Законы Моргана:

Поглощение 1:
Поглощение 0:
Поглощения:

Скачать презентацию

Разделы презентаций

Основы логики(теория)

Содержание

Слайды и текст этой презентации

Слайд 1ОСНОВЫ ЛОГИКИУчитель информатики МБОУ «Великомихайловская СОШ Новооскольского района Белгородской области»

Ерошенко И.В.ТЕОРИЯ

Слайд 2ОпределениеЛогика – это наука о формах и способах мышленияФормы мышленияпонятиесуждение(высказывание,

утверждение)умозаключение

Слайд 3ПонятиеПонятие – это форма мышления, фиксирующая основные, существенные признаки объекта;Понятие

имеет две стороны: содержание и объем;Содержание – это совокупность существенных

Слайд 4ВысказываниеВысказывание – это форма мышления, в которой что-либо утверждается или

отрицается о реальных предметах, их свойствах и отношениях между ними;Высказывание

Слайд 5Вопросительные и восклицательные предложения не являются высказываниями, т.к. в них

ничего не утверждается и не отрицаетсяНапример:Нельзя касаться оголенных проводов!Когда закончится

Слайд 6УмозаключениеУмозаключение – это форма мышления, с помощью которой из одного

или нескольких высказываний может быть получено новое суждение;Посылками умозаключения могут

Слайд 7Алгебра высказыванийСлужит для определения истинности или ложности составных высказываний, не

вникая в их содержание;В алгебре высказываний простым высказываниям ставятся в

Слайд 8Логические операцииЛогическое умножениеОбъединение двух (или нескольких) высказываний в одно с

помощью союза «и» («а», «но») называется операцией логического умножения или

Слайд 9Обозначение операции логического умножения: &, ^, *;Пусть имеется два простых

высказывания A и B, составим составное высказывание F с помощью

Слайд 10Таблица истинности

Слайд 11Логическое сложениеОбъединение двух (или нескольких) высказываний в одно с помощью

союза «или» называется операцией логического сложения или дизъюнкцией.Правило истинностиСоставное высказывание,

Слайд 12Обозначение операции логического сложения: ; +;Пусть имеется два простых высказывания

A и B, составим составное высказывание F с помощью дизъюнкции:

Слайд 13Таблица истинности

Слайд 14Логическое отрицаниеПрисоединение частицы «не» к высказыванию называется операцией логического отрицания

или инверсиейПравило истинностиЛогическое отрицание (инверсия) делает истинное высказывание ложным, а

Слайд 15Таблица истинности

Слайд 16Логическое следованиеСоединение двух высказываний в одно с помощью оборота речи

«если…, то…» называется операцией логического следования или импликациейПравило истинностиСоставное высказывание,

Слайд 17Обозначение импликации: ,  Формула: F = A  BТаблица