Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поиск и отбор информации. Методы поиска. Критерии отбора. Формула включений исключений
Содержание
- 1. Поиск и отбор информации. Методы поиска. Критерии отбора. Формула включений исключений
- 2. Величиной называется все что может быть измерено
- 3. понедельник
- 4. Музыкальные инструменты
- 5. Цвета
- 6. Слайд 6
- 7. Множество живых существСоставь множество из соответствующих элементов
- 8. Множество всех действительных чисел Эйлер изобразил с
- 9. Слайд 9
- 10. Леонард Эйлер, крупнейший математик XVIII века,
- 11. С1761 по 1768 год им были написаны
- 12. После Эйлера этот же метод
- 13. Слайд 13
- 14. "Обитаемый остров" и "Стиляги"
- 15. РешениеЧертим два множества таким образом: 6 человек,
- 16. 4. Графический методЗадача 1. В классе 30
- 17. Для двух конечных множеств А и В
- 18. Для трех конечных множеств А, В и С формула включений и исключений принимает вид: N(ABC)=N(A)+N(B)+N(C)-N(AB)-N(AC)-N(BC)+N(ABC)
- 19. Пример1: На вступительном экзамене по математике были
- 20. Решение. Пусть U — множество всех абитуриентов,
- 21. http://900igr.net/prezentacija/algebra/elementy-teorii-mnozhestv-216273/primer1-na-vstupitelnom-ekzamene-po-matematike-byli-predlozheny-tri-58.htmlhttp://www.myshared.ru/slide/94043http://logika.vobrazovanie.ru/index.php?link=kr_e.htmlhttp://reshizadachu.ucoz.ru/index/krugi_ehjlera/0-18http://mypresentation.ru/documents/a7acfb257e0a2409dc0254ee48762c0f/img7.jpg Ресурсы:
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Поиск и отбор информации. Методы поиска. Критерии отбора. Формула включений
исключений
обл., Некрасовского р-наСлайд 2Величиной называется все что может быть измерено и выражено числом.
Множеством
называется совокупность некоторых элементов. Элементами множества могут быть числа, фигуры,
предметы, понятия и т.п.Определение множества
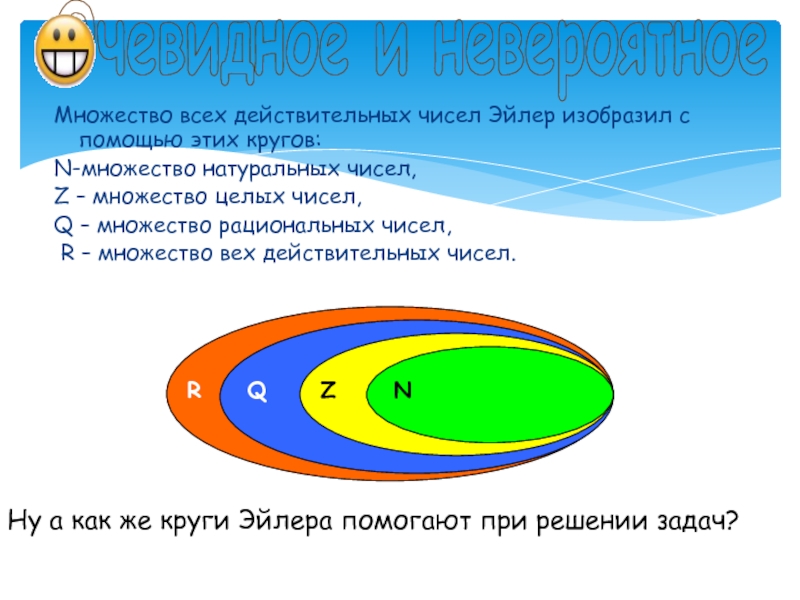
Слайд 8Множество всех действительных чисел Эйлер изобразил с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q –
множество рациональных чисел,R – множество вех действительных чисел.
Очевидное и невероятное
Ну а как же круги Эйлера помогают при решении задач?
R
Q
Z
N
Слайд 10 Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В
1727г. по приглашению Петербургской академии наук он приехал в Россию.
Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.Леонард Эйлер
Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).
(1707 г.-1783 г.)
Слайд 11С1761 по 1768 год им были написаны знаменитые «Письма к
немецкой принцессе», где Эйлер как раз и рассказывал о своем
методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения». Понятно, что слово «круг» здесь весьма условно, множества могут изображаться на плоскости в виде произвольных фигур.Слайд 12
После Эйлера этот же метод разрабатывал чешский математик
Бернард Больцано (1781 – 1848). Только в отличие от Эйлера
он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.Слайд 14 "Обитаемый остров" и "Стиляги"
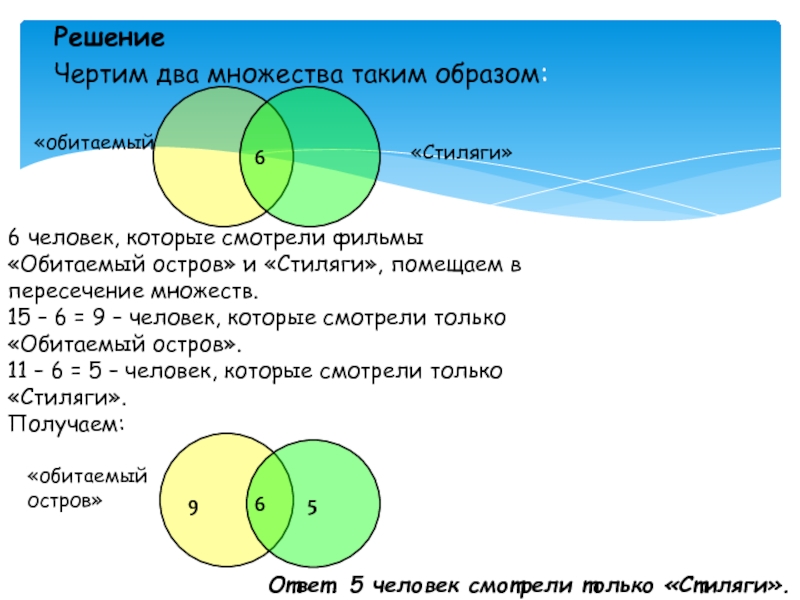
Некоторые ребята
из нашего класса любят ходить в кино. Известно, что 15
ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?Решение задач
Слайд 15Решение
Чертим два множества таким образом:
6 человек, которые смотрели фильмы
«Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 –
6 = 9 – человек, которые смотрели только «Обитаемый остров». 11 – 6 = 5 – человек, которые смотрели только «Стиляги». Получаем:Ответ. 5 человек смотрели только «Стиляги».
6
«обитаемый остров»
«Стиляги»
«обитаемый остров»
«Стиляги»
9
6
5
Слайд 164. Графический метод
Задача 1. В классе 30 учащихся, 16 из
них играют в шахматы, 17 увлекаются теннисом, а 10 занимаются
и шахматами и теннисом. Есть ли в классе ученики, равнодушные к шахматам и к теннису, и если есть, то сколько их?Учащиеся, играющие в шахматы: N1+N2=16
Учащиеся, играющие в теннис: N3+N2=17
Учащиеся, играющие и в шахматы и в теннис: N2=10
Решение:
Учащиеся, играющие только в шахматы: N1=16-N2=16-10=6
Учащиеся, играющие только в теннис:N3=17-N2=17-10=7
Всего учащихся, играющих и в шахматы и в теннис: N1+N2+N3=23
Количество учащихся, не играющих ни в шахматы, ни в теннис: 30-23=7
Слайд 17Для двух конечных множеств А и В количество элементов принадлежащих
множеству А равно N(A), а принадлежащих множеству В – N(B).
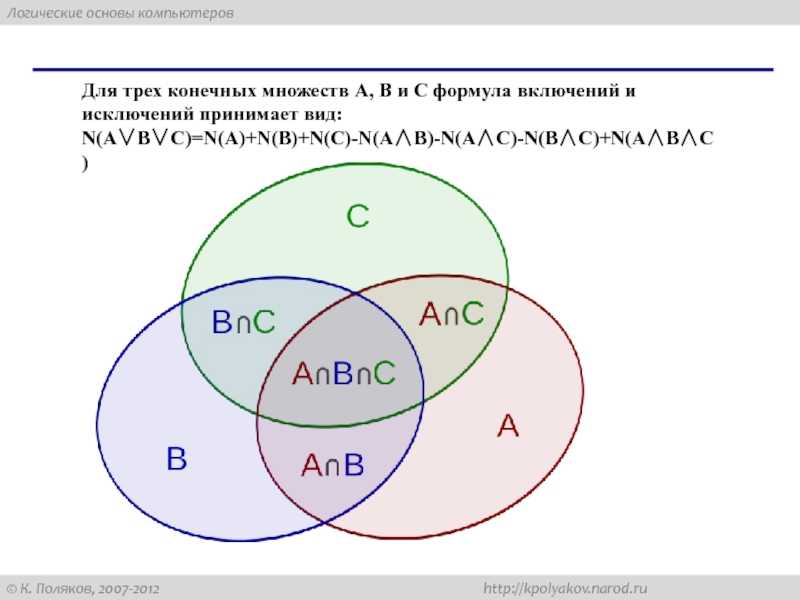
Количество элементов, принадлежащих и множеству А и множеству В равно N(AB). Для того, чтобы количество элементов, принадлежащих обеим множествам не учитывалось дважды, необходимо из суммы количества элементов множества А и множества В вычесть количество элементов, принадлежащих обеим множествам: N(АВ)=N(А)+N(B)-N(АВ)Слайд 18Для трех конечных множеств А, В и С формула включений
и исключений принимает вид:
N(ABC)=N(A)+N(B)+N(C)-N(AB)-N(AC)-N(BC)+N(ABC)
Слайд 19Пример1: На вступительном экзамене по математике были предложены три задачи:
по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов задачу по
алгебре решили 800, по планиметрии — 700, а по стереометрии — 600 абитуриентов. При этом задачи по алгебре и планиметрии решили 600 абитуриентов, по алгебре и стереометрии — 500, по планиметрии и стереометрии — 400. Все три задачи решили 300 абитуриентов. Существуют ли абитуриенты, не решившие ни одной задачи, и если да, то сколько их?Решите задачу
Слайд 20Решение. Пусть U — множество всех абитуриентов, А —. множество
абитуриентов, решивших задачу по алгебре, В — множество абитуриентов, решивших
задачу по планиметрии, С — множество абитуриентов, решивших задачу по стереометрии. По условию n(U) =1000, n(A) = 800, n(В)=700, n(С)=600, n(AB)= 600, n(AC) = 500, n(BC) = 400, n(ABC) =300. В множество ABC включены все абитуриенты, решившие хотя бы одну задачу. По формуле (2) имеем:n(А U В U С) = 800 + 700 + 600 - 600 - 500 - 400 + 300 =900.
Отсюда следует, что не все поступающие решили хотя бы одну задачу. Ни одной задачи не решили
n(U) - n(AUBUC)=1000 - 900=100 (абитуриентов).