Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку Логические выражения и таблицы истинности
Содержание
- 1. Презентация к уроку Логические выражения и таблицы истинности
- 2. Логические выражения. Каждое составное высказывание можно выразить
- 3. Запишем в форме логического выражения составное высказывание
- 4. Логическое выражение F = ( А v В)
- 5. Таблицы истинности. Для каждого составного высказывания (логического выражения)
- 6. При построении таблиц истинности целесообразно руководствоваться определенной
- 7. Во- вторых, необходимо определить количество столбцов в
- 8. Таблица истинности логической функции F = ( А v В) & (A v B).
- 9. Равносильные логические выражения. Логические выражения, у которых последние
- 10. Таблица истинности логического выражения A & B
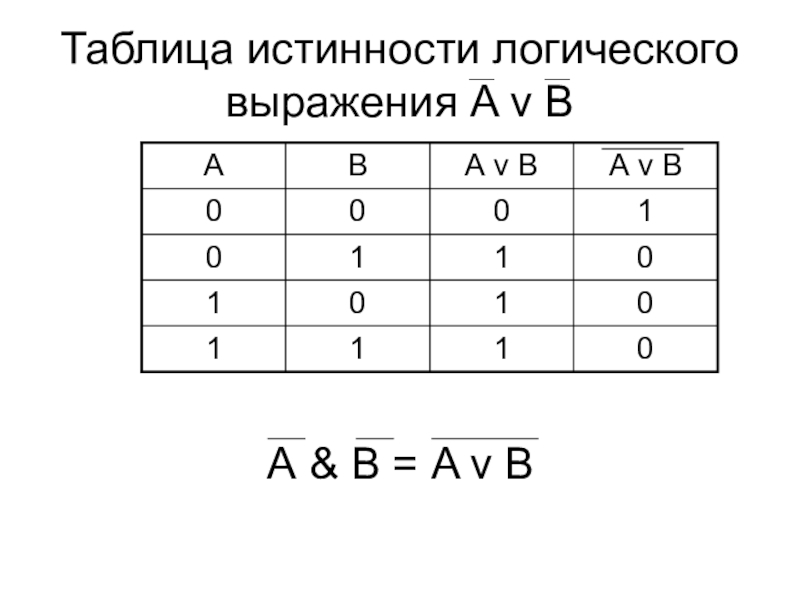
- 11. Таблица истинности логического выражения A v BА & В = A v B
- 12. Скачать презентанцию
Логические выражения. Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Слайды и текст этой презентации
Слайд 3 Запишем в форме логического выражения составное высказывание
«(2 · 2
= 5 или 2 · 2 = 4) и (2
· 2 ≠ 5 или 2 · 2 ≠ 4)»Данное высказывание выглядит следующим образом:
А = «2 · 2 = 5» - ложно (0)
В = «2 · 2 = 4» - истинно (1)
Тогда составное высказывание выглядит:
«(А или В ) и (А или В) »
Слайд 4Логическое выражение
F = ( А v В) & (A v
B).
Истинность или ложность составных высказываний можно определить чисто формально, руководствуясь
законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.F = ( А v В) & (A v B) = ( 0 v 1) & (1 v 0) = 1 & 1 = 1
Слайд 5Таблицы истинности.
Для каждого составного высказывания (логического выражения) можно построить таблицу
истинности, которая определяет его истинность или ложность при всех возможных
комбинациях исходных значений простых высказываний (логических переменных).Слайд 6 При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.
Во –первых,
необходимо определить количество строк в таблице истинности. Оно равно количеству
возможных комбинаций значений логических переменных, входящих в логическое выражение.количество строк = 2n
В нашем случае логическая функция
F = ( А v В) & (A v B) имеет 2 переменные и, следовательно количество строк в таблице истинности должно быть равно 4.
Слайд 7Во- вторых, необходимо определить количество столбцов в таблице истинности, которое
равно количеству логических переменных плюс количество логических операций.
В нашем случае
количество переменных равно двум, а количество логических операций – пяти, то есть количество столбцов таблицы истинности равно семи.В – третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных.
В- четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Слайд 9Равносильные логические выражения.
Логические выражения, у которых последние столбцы таблиц истинности
совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак
«=».Докажем, что логические выражения А & B и A v B