Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Основы логики"
Содержание
- 1. "Основы логики"
- 2. Формы мышленияПервые учения о формах и способах
- 3. Законы логики отражают в сознании человека свойства,
- 4. ПОНЯТИЕ.ЭТО ФОРМА МЫШЛЕНИЯ, ФИКСИРУЮЩАЯ ОСНОВНЫЕ,
- 5. ПОНЯТИЕ- имеет две стороны: содержание, объем.Например,
- 6. Высказываниеэто форма мышления, в которой что-либо
- 7. Умозаключениеэто форма мышления, с помощью которой
- 8. Вопросы.Какие существуют основные формы мышления?В чем состоит
- 9. Алгебра высказыванийАлгебра высказываний была разработана для
- 10. А = "Два умножить на два равно
- 11. В алгебре высказываний высказывания обозначаются
- 12. Конъюнкция (логическое умножение).Объединение двух (или нескольких) высказываний
- 13. «ИСТИНА» ?
- 14. Дизъюнкция (логическое сложение).Объединение двух (или нескольких) высказываний
- 15. «ИСТИНА» ?
- 16. Инверсия (логическое отрицание)Присоединение частицы «не» к высказыванию
- 17. Импликация (логическое следование) в естественном
- 18. Эквиваленция (равнозначность)· в естественном языке соответствует оборотам речи
- 19. Пример№ 1Высказывание : С= «Летом я поеду
- 20. Логические выражения Составные высказывания в алгебре логики
- 21. Запишите высказывания с помощью символов логики высказываний,
- 22. Определение: Таблицу, показывающую, какие значения принимает составное
- 23. Алгоритм построения таблицы истинности: 1) подсчитать количество
- 24. Пример . Для формулы A&(B ∨ ¬
- 25. Выполни самостоятельно следующие задания:В рабочей тетради:1. Построить
- 26. Пример. Определите истинность составного высказывания: ( Ā
- 27. Правильно!
- 28. Неверный ответ!!!
- 29. Водород бесцветен и не имеет запаха, тогда
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Основы логики
Оглавление:
Формы мышления.
Понятие
Умозаключение
Высказывание
Алгебра высказываний
Логические операции :
Конъюнкция
Дизъюнкция
Инверсия
Импликация
Эквиваленция
Логические выражения и таблицы
истинности.
Слайд 2Формы мышления
Первые учения о формах и способах рассуждений возникли в
странах Древнего Востока (Китай, Индия), но в основе современной логики
лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи ) от его содержания.Логика - это наука о формах
и способах мышления.
?
Слайд 3Законы логики отражают в сознании человека свойства, связи и отношения
объектов окружающего мира. Логика позволяет строить формальные модели окружающего мира,
отвлекаясь от содержательной стороны.Мышление всегда осуществляется в каких-то формах.
Основными формами мышления являются :
ПОНЯТИЕ
ВЫСКАЗЫВАНИЕ
УМОЗАКЛЮЧЕНИЕ
Слайд 4ПОНЯТИЕ.
ЭТО ФОРМА МЫШЛЕНИЯ,
ФИКСИРУЮЩАЯ ОСНОВНЫЕ,
СУЩЕСТВЕННЫЕ ПРИЗНАКИ
ОБЪЕКТА.
Например,
понятие «компьютер» объединяет множество электронных устройств, которые предназначены для обработки
информации и обладают монитором и клавиатурой. Даже по этому короткому описанию компьютер трудно спутать с другими объектами, например механизмами, служащими для перемещения по дорогам и хранящимися в гаражах, которые объединяются понятием «автомобиль».?
Слайд 5ПОНЯТИЕ- имеет две стороны:
содержание, объем.
Например, содержание понятия «персональный компьютер»
можно раскрыть следующим образом: «Персональный компьютер - это универсальное электронное
средство для автоматической обработки информации, предназначенное для одного пользователя».Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.
Слайд 6Высказывание
это форма мышления, в которой
что-либо утверждается или отрицается о
свойствах реальных предметов и отношениях между ними. Высказывание
может быть либо истинно, либо ложно.Например. «Два умножить на два равно четыре», это высказывание на естественном языке. «2*2=4»- высказывание на формальном языке.
«Процессор является устройством обработки информации» - истинное высказывание. «Процессор является устройством печати» - ложное высказывание.
?
Слайд 7Умозаключение
это форма мышления, с помощью
которой из одного или нескольких
суждений
(посылок) может быть получено новое суждение
(заключение)
Например, если
мы имеем суждение « Все углы треугольника равны», то мы можем путем умозаключения доказать, что в этом случае справедливо суждение «Этот треугольник равносторонний». Посылками умозаключения по правилам формальной логики могут быть только истинные суждения.?
Слайд 8Вопросы.
Какие существуют основные формы мышления?
В чем состоит разница между содержанием
и объемом понятия?
Может ли высказывание выражено в форме вопросительного предложения?
Как
определяется истинность или ложность простого высказывания? Составного высказывания?Слайд 9Алгебра
высказываний
Алгебра высказываний была разработана для того, чтобы можно было
определять истинность или ложность составных высказываний, не вникая в их
содержание.В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита.
Слайд 10А = "Два умножить на два равно четырем"
В = "Два
умножить на два равно пяти"
Высказывания могут быть истинными или ложными.
Истинному высказыванию соответствует значение логической переменной 1, а ложному – значение 0.А = "Два умножить на два равно четырем"
В = "Два умножить на два равно пяти"
Истина А=1
Ложь В=0
Рассмотрим два простых высказывания.
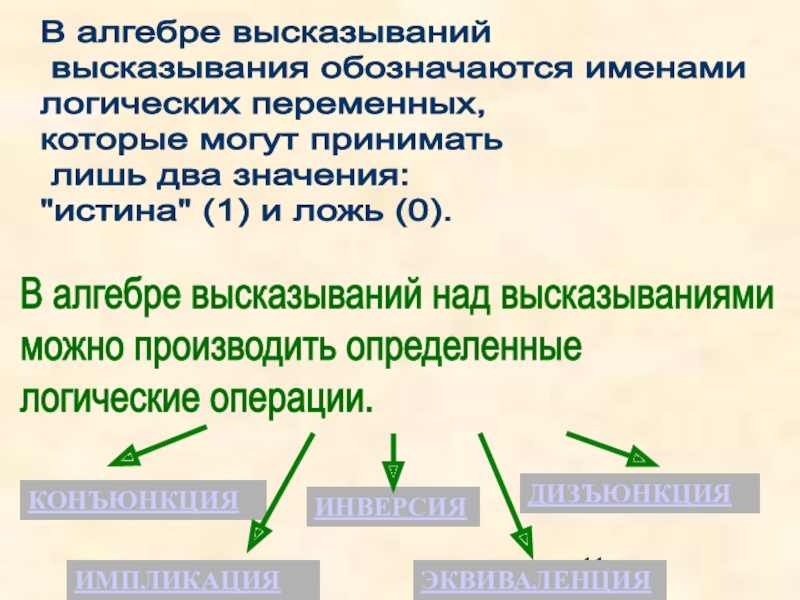
Слайд 11В алгебре высказываний высказывания обозначаются именами логических переменных, которые
могут принимать лишь два значения: "истина" (1) и ложь
(0).В алгебре высказываний над высказываниями
можно производить определенные
логические операции.
КОНЪЮНКЦИЯ
ДИЗЪЮНКЦИЯ
ИНВЕРСИЯ
ИМПЛИКАЦИЯ
ЭКВИВАЛЕНЦИЯ
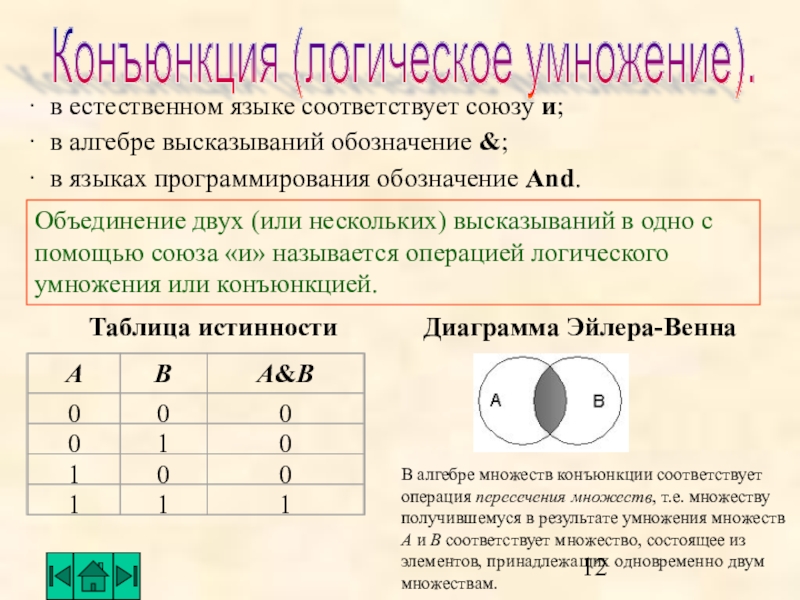
Слайд 12Конъюнкция (логическое умножение).
Объединение двух (или нескольких) высказываний в одно с
помощью союза «и» называется операцией логического умножения или конъюнкцией.
· в
естественном языке соответствует союзу и; · в алгебре высказываний обозначение &;
· в языках программирования обозначение And.
Таблица истинности
Диаграмма Эйлера-Венна
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Слайд 13«ИСТИНА» ?
«ЛОЖЬ»?
"(1) 2*2=5 И 3*3=10"
"(2) 2*2=5 И 3*3=9"
"(3) 2*2=4 И 3*3=10"
"(4) 2*2=4 И 3*3=9"
Фигура желтого цвета –истина
Фигура зеленого цвета – ложь.
Проверь себя!
Слайд 14Дизъюнкция (логическое сложение).
Объединение двух (или нескольких) высказываний в одно с
помощью союза «или» называется операцией логического сложения или дизъюнкцией.
в
естественном языке соответствует союзу или; обозначение ∨ ;
в языках программирования обозначение Or.
Таблица истинности
Диаграмма Эйлера-Венна
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Слайд 15«ИСТИНА» ?
«ЛОЖЬ»?
"(1) 2*2=5 ИЛИ 3*3=10"
"(2) 2*2=5 ИЛИ 3*3=9"
"(3) 2*2=4 ИЛИ 3*3=10"
"(4) 2*2=4 ИЛИ 3*3=9"
Фигура желтого цвета –истина
Фигура зеленого цвета – ложь.
Проверь себя!
Слайд 16Инверсия (логическое отрицание)
Присоединение частицы «не» к высказыванию называется операцией логического
отрицания или инверсией.
Логическое отрицание (инверсия) делает истинное высказывание ложным и,
наоборот, ложное –истинным.F=А
в естественном языке соответствует словам неверно, что... и частице не;
обозначение Ā ;
в языках программирования обозначение Not;
Таблица истинности
Диаграмма Эйлера-Венна
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество , дополняющее его до универсального множества.
Слайд 17Импликация (логическое следование)
в естественном языке соответствует обороту
если ..., то ...;
· обозначение ⇒ .
Импликация -
это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. Пример.
«Если выглядит солнце, то станет тепло»
А= «Выглянет солнце»
В= «станет тепло»
А ⇒ В
Слайд 18Эквиваленция (равнозначность)
· в естественном языке соответствует оборотам речи тогда и только
тогда; в том и только в том случае;
· обозначения
⇔ , ~ . Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности эквиваленции:
Пример :«Людоед голоден тогда и только тогда, когда он давно не ел».
А =«людоед голоден»
В =«он давно не ел»
А ⇔ В
Слайд 19Пример№ 1
Высказывание : С= «Летом я поеду в деревню или
в туристическую поездку».
А =«летом я поеду в деревню»
В =
«летом я поеду в туристическую поездку» Тогда С = А V В.
Пример № 2
С =«Неверно,что 4 делится на 3»
А= «4 делится на 3»
С = Ā
Пример №3.
Вычислить значение логической формулы:
К = Ā и В или А и С,
где А=ложь, В = истина, С=истина
К = Ā & В v А & С = 1 & 1 v 0 & 1 = 1 (истина).
Слайд 20Логические выражения
Составные высказывания в алгебре логики записываются с помощью
логических выражений.
Логическое выражение – это запись, которая содержит логические переменные,
обозначающие высказывания и знаки логических операций, обозначающие логические функции.Для записи составного выражения необходимо:
Выделить простые высказывания;
Выделить логические связи между ними;
Слайд 21Запишите высказывания с помощью символов логики высказываний, обозначив простые высказывания
P, Q, M, N, L, S, T
Водород бесцветен и не
имеет запаха, тогда и только тогда, когда 7х7 = 49 и яблоко – фрукт. Прозрачный лес один чернеет, И ель сквозь иней зеленеет, И речка подо льдом блестит.
(А.С.Пушкин)
3. В свободное время я люблю играть в волейбол или в шахматы.
Проверь!
Слайд 22Определение: Таблицу, показывающую, какие значения принимает составное высказывание при всех
сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей
истинности составного высказывания.Для любого логического выражения достаточно просто построить таблицу истинности.
Таблицы истинности.
Слайд 23
Алгоритм построения таблицы истинности:
1) подсчитать количество переменных n в
логическом выражении;
2) определить число строк в таблице, которое равно
m = 2n; 3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
5) заполнить столбцы входных переменных наборами значений;
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции.
Порядок выполнения логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.
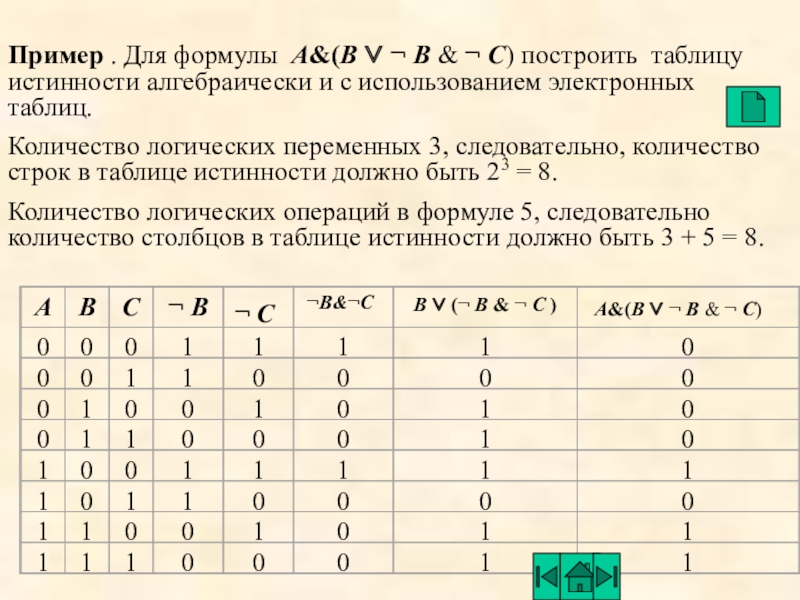
Слайд 24Пример . Для формулы A&(B ∨ ¬ В & ¬
C) построить таблицу истинности алгебраически и с использованием электронных таблиц.
Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8.
Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.
¬ С
A&(B ∨ ¬ В & ¬ C)
Слайд 25Выполни самостоятельно следующие задания:
В рабочей тетради:
1. Построить таблицы истинности для
следующих формул:
а) A ∨ (B ∨ ¬ В
⇒ ¬С ) б) A & (B & ¬В ⇒ ¬С )
в) A ∨ (B ∨ ¬В ) & A ∨ (B ⇒ ¬С )
2. Выбрать составное высказывание, имеющее ту же таблицу истинности, что и не (не A и не(B и C)).
1) A и B или C и A;
2) (A или B) и (A или C);
3) A и (B или C);
4) A или (не B или не C);
В электронных таблицах:
Докажите с помощью таблиц истинности равносильность следующих логических выражений:
а) (А ⇒ В) & (А ∨ ¬В ); б) (А ⇔ В) & (А&В) ∨ (¬А & ¬В ).
Слайд 26Пример. Определите истинность составного высказывания: ( Ā &Ē ) &
(C ∨D), состоящего из простых высказываний:
А = {Принтер –
устройство вывода информации}, Е = {Процессор – устройство хранения информации},
С = {Монитор – устройство вывода информации},
D = {Клавиатура – устройство обработки информации}.
Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний: А = 1, Е = 0, С = 1, D = 0.
Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:
( Ā &Ē ) &(1∨ 0) = ( 0& 1) & ( 1∨ 0 ) = 0
Составное высказывание ложно.
Слайд 29Водород бесцветен и не имеет запаха, тогда и только тогда,
когда 7х7 = 49 и яблоко – фрукт.
(P V
Q) ⇔(M & N)2. Прозрачный лес один чернеет, И ель сквозь иней зеленеет, И речка подо льдом блестит.
(P & Q & M)
(А.С.Пушкин)
3. В свободное время я люблю играть в волейбол или в шахматы.
(PVQ)
Проверь себя!