Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Программные средства интерактивной геометрии
Содержание
- 1. Программные средства интерактивной геометрии
- 2. Компьютерные программы по геометрииWingeomGeogebraЖивая геометрияPolyKigМатематический конструктор 1С
- 3. Wingeom (Wgeomru)Лицензия: Freeware 1985-2009(свободное пользование)Автор: Richard ParrisЯзык интерфейса: русскийСайт: http://math.exeter.edu/rparrisОписание: Wingeom
- 4. Программа Wingeom обладает возможностями: 1)создавать точные, аккуратные
- 5. з) величина (в стерадианах) многогранного угла;
- 6. GeoGebra Категория: геометрическое ПОЯзык программирования: JavaПлатформа (ОС): Windows, Linux, MacOSНазвание
- 7. Систему можно использовать для построения линий: построение
- 8. Кроме графических действий в системе могут быть
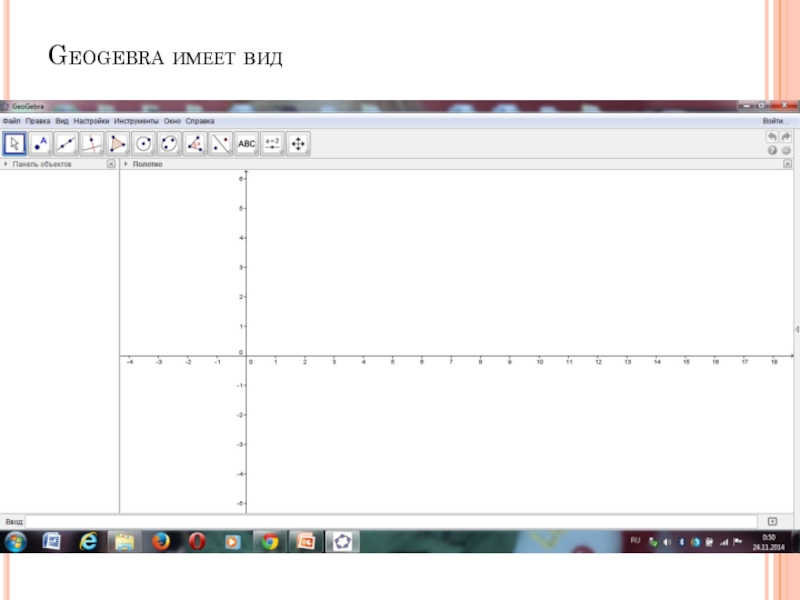
- 9. Geogebra имеет вид
- 10. Задача 1. Треугольник АВС задан точками: А(9;–5),
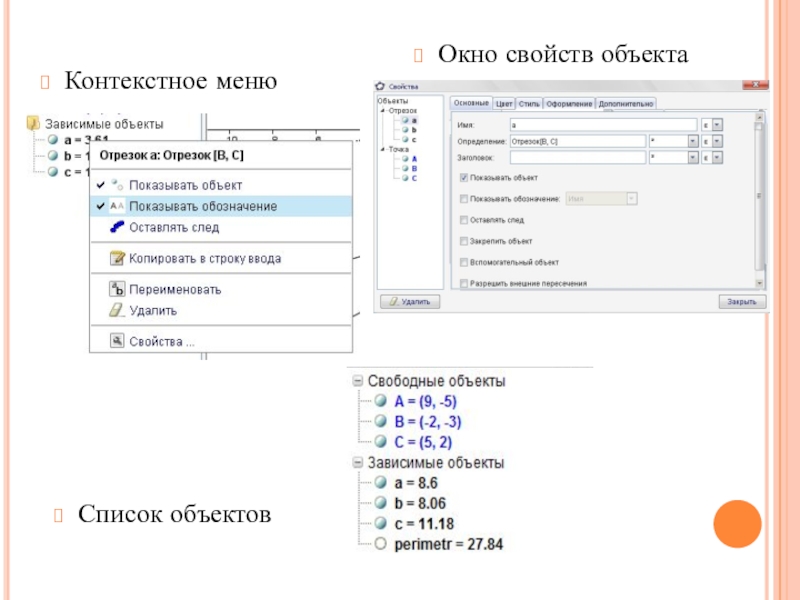
- 11. Контекстное менюОкно свойств объектаСписок объектов
- 12. построить вершины треугольника АВСА=(9, –5) В=(–2, –3) С=(5, 2)
- 13. построить стороны треугольника AB, BC,AC
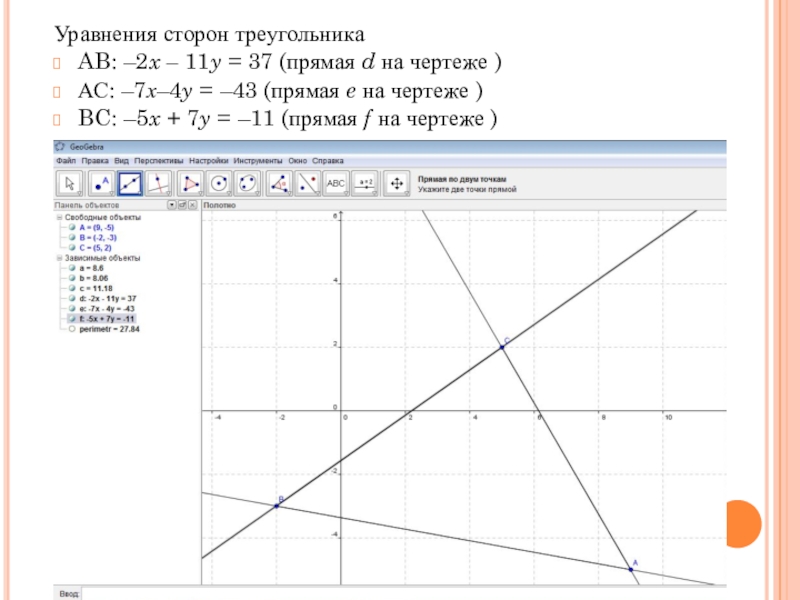
- 14. Уравнение сторон треугольника
- 15. Уравнения сторон треугольникаAB: –2x – 11y = 37 (прямая d на
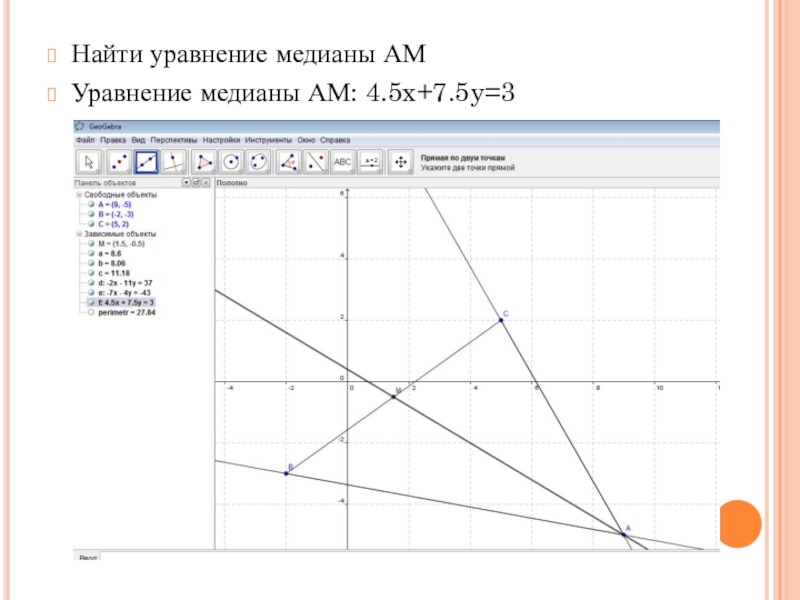
- 16. Найти уравнение медианы АМУравнение медианы АМ: 4.5x+7.5y=3
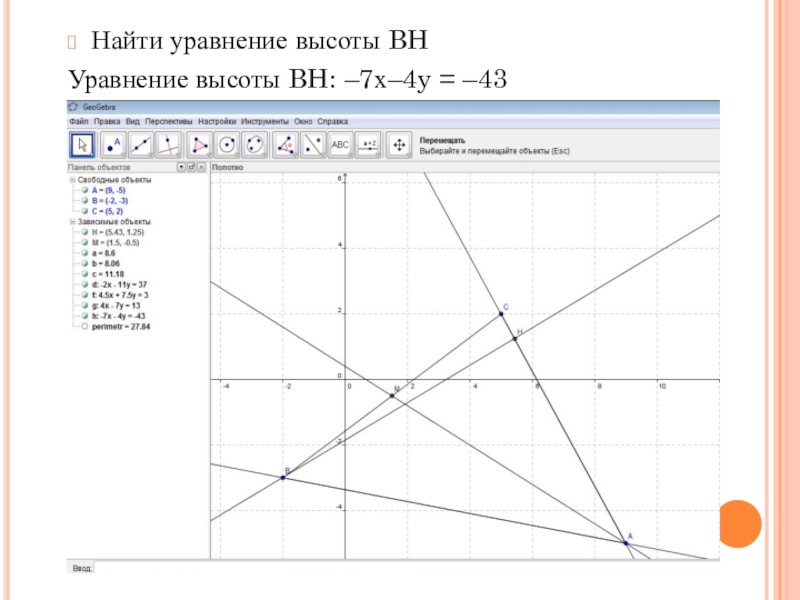
- 17. Найти уравнение высоты BH Уравнение высоты BH: –7х–4y = –43
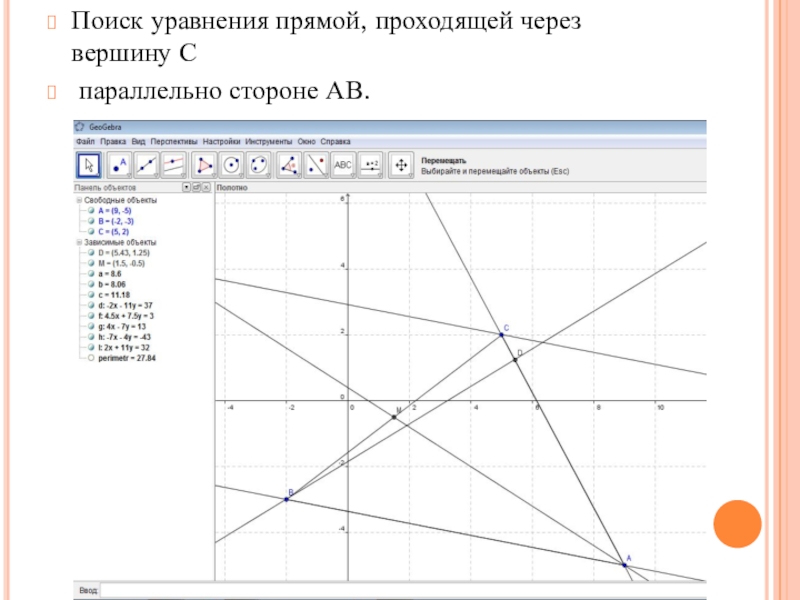
- 18. Поиск уравнения прямой, проходящей через вершину С параллельно стороне АВ.
- 19. Найти радиус описанной окружности
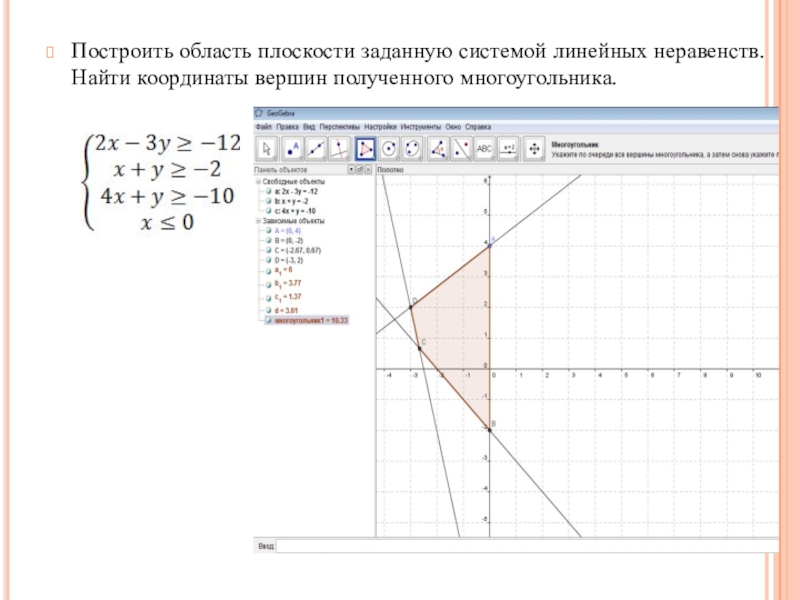
- 20. Построить область плоскости заданную системой линейных неравенств. Найти координаты вершин полученного многоугольника.
- 21. «The Geometer's Sketchpad» "Живая геометрия"
- 22. «Живая геометрия» - это набор инструментов, который
- 23. Слева расположен панель инструментов
- 24. Слайд 24
- 25. Постороение уравнениий F(y)=5y^2+10y+6
- 26. Слайд 26
- 27. Слайд 27
- 28. Poly Название программы: PolyПлатформа (ОС): WindowsНазвание компании: Pedagoguery SoftwareЛицензия: условно бесплатнаяСайт: http:// www.peda.com/polyЯзык интерфейса: английский
- 29. Poly - программа для того, чтобы исследовать
- 30. Слайд 30
- 31. «Интерактивная геометрия (Kig)»Kig - приложение для интерактивных геометрических построений,
- 32. Построение объектов Построение точекВы можете сделать это
- 33. Построение других объектовВы можете построить определённый объект,
- 34. Выбор объектовЕсть два способа выбора объекта:Вы можете
- 35. НадписиДля создания надписи нажмите соответствующую кнопку на
- 36. «Математический конструктор 1С»«Математический конструктор» – незаменимый помощник
- 37. Возможности «Математического конструктора»: Динамические геометрические построенияИзмерения и
- 38. Спасибо за внимание!
- 39. Скачать презентанцию
Компьютерные программы по геометрииWingeomGeogebraЖивая геометрияPolyKigМатематический конструктор 1С
Слайды и текст этой презентации
Слайд 2Компьютерные программы по геометрии
Wingeom
Geogebra
Живая геометрия
Poly
Kig
Математический конструктор 1С
Слайд 3Wingeom
(Wgeomru)
Лицензия: Freeware 1985-2009
(свободное пользование)
Автор: Richard Parris
Язык интерфейса: русский
Сайт: http://math.exeter.edu/rparris
Описание: Wingeom является геометрической программой и
Слайд 4Программа Wingeom обладает возможностями:
1)создавать точные, аккуратные модели плоских и пространственных
фигур: а) с использованием координат точек (вершин) фигуры; б) заданием
готовых фигур; в) удалением элементов из готовой фигуры; г) добавлением элементов к готовой фигуре; д) создание сечений пространственных фигур.2)трансформировать готовые изображения: а) способ изменения изображения (дискретный, непрерывный); б) вид изображения пространственных фигур (в центральной проекции, параллельной проекции, ортогональной проекции); в) перемещение фигуры (удаление, приближение, наклон, вращение, смещение); г) анимация;
3)редактировать построенные модели: а) выделять (толщина, цвет, стрелки, невидимые линии); б) удалять элементы (точки, линейные элементы, криволинейные элементы);
4)производить необходимые измерения: а) длина отрезка; б) величина угла в градусах; в) площадь многоугольника; г) периметр многоугольника; д) отношение длин отрезков; е) координаты точки; ж) величина двугранного угла;
Слайд 5з) величина (в стерадианах) многогранного угла; и) длина дуги окружности;
к) длина окружности; л) площадь круга, сечения многогранника; м) радианная
мера угла; н) объем шара, конуса5)применять геометрические преобразования: а) параллельный перенос; б) нормальный перенос; в) поворот; г) гомотетия; д) зеркальная симметрия; е) инверсия;
6)работать с текстом и обозначениями точек: а) ввод и удаление текста и обозначений; б) редактирование текста и обозначений (цвет, тип шрифта, размер шрифта); в) привязка текста (к фигуре, к рамке);
7)сохранять историю создания модели; 8)показать построение модели в медленном режиме (презентация); 9)использовать макрос (макро-построения).
Слайд 6GeoGebra
Категория: геометрическое ПО
Язык программирования: Java
Платформа (ОС): Windows, Linux, MacOS
Название компании: Macrovision
Лицензия: GPL (General Public License)
свободно распространяемая лицензия
Авторы: Markus Hohenwarter (Австрия, США),
Сайт: http://www.geogebra.org/
Язык интерфейса: русский
Слайд 7Систему можно использовать для построения линий:
построение графиков функций y =
f (x);
построение конических сечений:
коника произвольного вида — по пяти
точкам.Окружность по центру и точке на ней, по центру и радиусу, по трем точкам;
эллипс – по двум фокусам и точке на кривой;
парабола – по фокусу и директрисе;
гипербола – по двум фокусам и точке на кривой;
Слайд 8Кроме графических действий в системе могут быть выполнены вычисления:
действия с
матрицами: сложение, умножение; транспонирование, инвертирование; вычисление определителя;
вычисления с комплексными числами;
нахождение
точек пересечения кривых;статистические функции:
вычисление математического ожидания, дисперсии;
вычисление коэффициента корреляции;
Аппроксимация множества точек кривой заданного вида: полином; экспонента; логарифм; синусоида.
Слайд 10Задача 1. Треугольник АВС задан точками: А(9;–5), В(–7;–8), С(–5;–2). С
помощью программы GeoGebra необходимо:
1) найти периметр треугольника;
2) найти уравнения сторон
треугольника;3) найти уравнение медианы АМ;
4) найти уравнение высоты BH;
5) найти уравнение прямой, проходящей через вершину A параллельно стороне ВC;
6) найти радиус описанной окружности.
Слайд 15Уравнения сторон треугольника
AB: –2x – 11y = 37 (прямая d на чертеже )
АС: –7х–4y = –43
(прямая e на чертеже )
BC: –5x + 7y = –11 (прямая f на чертеже
)Слайд 20Построить область плоскости заданную системой линейных неравенств. Найти координаты вершин
полученного многоугольника.
Слайд 21«The Geometer's Sketchpad»
"Живая геометрия"
Название программы: The Geometer's Sketchpad (русская версия "Живая
геометрия")
Исходное название файла: GSP 4.04.exe
Тип: интерактивное геометрическое ПО
Платформа (ОС): Mac OC X, Windows,
LinuxНазвание компании: Key Curriculum Press Technologies
Лицензия: свободное пользование (русская версия)
Автор: Nicholas Jackiw
Разработчики: Nicholas Jackiw, Skott Steketee
Сайт: www.keypress.com
Язык интерфейса: русский
Русификация: Институт новых технологий образования
Слайд 22«Живая геометрия» - это набор инструментов, который предоставляет все необходимые
средства для построения чертежей и их исследования. Она дает возможность
«открывать» и проверять геометрические факты. Программа позволяет "оживлять" чертежи, плавно изменяя положение исходных точек.Слева расположен панель инструментов
При помощи инструмента «точка» можно ставить различные точки.
При помощи «циркуля» рисовать окружности разных размеров
При помощи «линейка» можно размещать на чертеже линейные объекты: отрезки, лучи и другие прямые
Инструмент «текст» позволяет создавать надписи на чертеже ,с его помощью так же можно давать имена геометрическим объектам
С помощью «стрелки» можно передвинуть один объект или несколько элементов чертежа
В Верхней части окна расположена строка мен.
Слайд 28Poly
Название программы: Poly
Платформа (ОС): Windows
Название компании: Pedagoguery Software
Лицензия: условно бесплатная
Сайт: http:// www.peda.com/poly
Язык интерфейса: английский
Слайд 29 Poly - программа для того, чтобы исследовать многогранные поверхности. Программа
может показать многогранные поверхности тремя главными способами: • как трехмерное изображение, •
как плоская, двумерная развертка, и • как топологическое вложение в плоскость.Трехмерные изображения могут в интерактивном режиме вращаться, сворачиваясь/разворачиваясь. Физические модели могут быть произведены, если распечатать плоские двумерные развертки, разрезать по периметру, свернуть по краям, и склеить лентой вместе соседние грани.
Poly включает все особенности Poly и добавляет способность экспортировать многогранные модели, используя стандартные 3d форматы файлов (DXF, STL, 3DMF). С программой Pro Poly Вы можете также экспортировать вращающиеся многогранники как анимационные файлы GIF. Статические изображения могут экспортироваться как GIF или PCX файлы.
Слайд 31«Интерактивная геометрия (Kig)»
Kig - приложение для интерактивных геометрических построений, позволяющее ученикам и
студентам изучать геометрические фигуры с помощью компьютера.
Программа позволяет:
а) исследовать и
строить различные многогранники и их развертки;
б) перемещать и вращать многогранные тела;
в) распечатать развертки, которые можно вырезать и сложить для получения трехмерных моделей;
г) создавать Платоновы тела (тетраэдр, гексаэдр, октаэдр, додекаэдр и икосаэдр), Архимедовы тела (усеченный тетраэдр, кубооктаэдр, усеченный куб, и многое другое), призмы и антипризмы (треугольные, пятиугольные, шестигранные и т.д.).
д) генерировать Джонсона тела и многое другое. Слайд 32Построение объектов
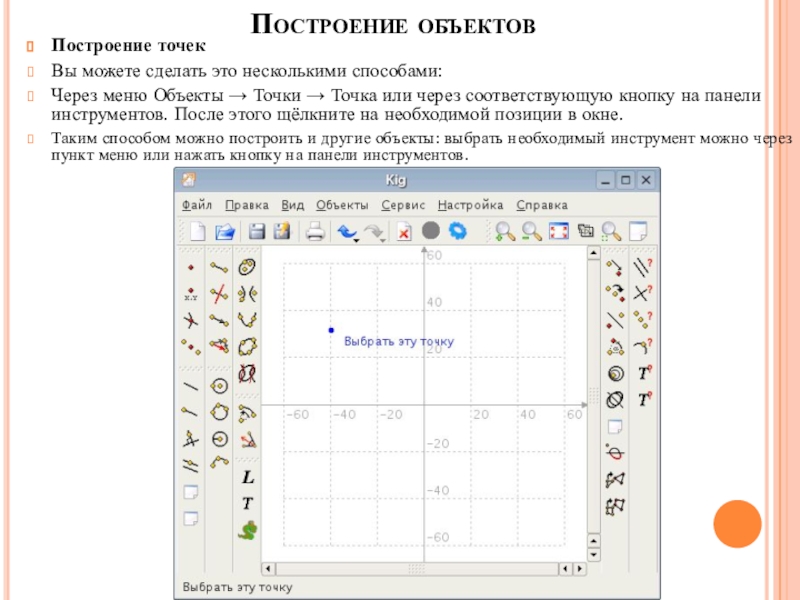
Построение точек
Вы можете сделать это несколькими способами:
Через меню Объекты → Точки → Точка или через
соответствующую кнопку на панели инструментов. После этого щёлкните на необходимой
позиции в окне.Таким способом можно построить и другие объекты: выбрать необходимый инструмент можно через пункт меню или нажать кнопку на панели инструментов.
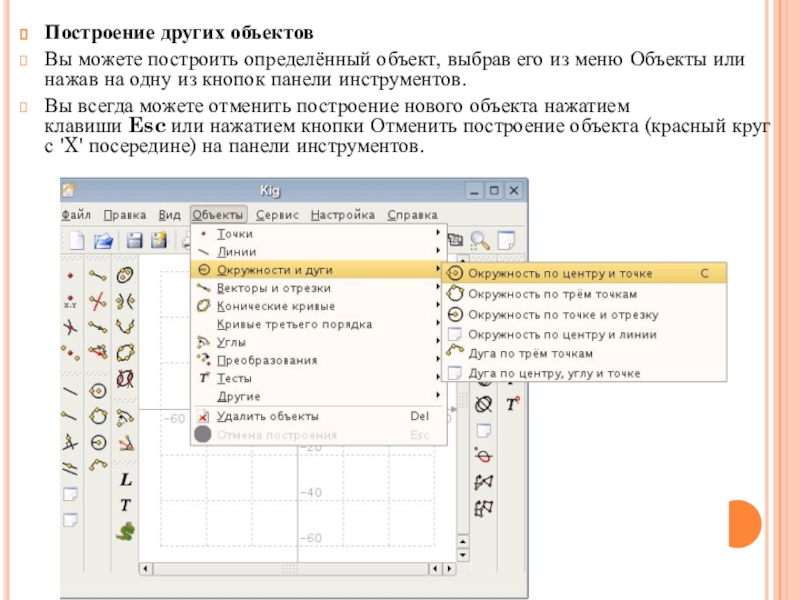
Слайд 33Построение других объектов
Вы можете построить определённый объект, выбрав его из
меню Объекты или нажав на одну из кнопок панели инструментов.
Вы всегда можете
отменить построение нового объекта нажатием клавиши Esc или нажатием кнопки Отменить построение объекта (красный круг с 'X' посередине) на панели инструментов.
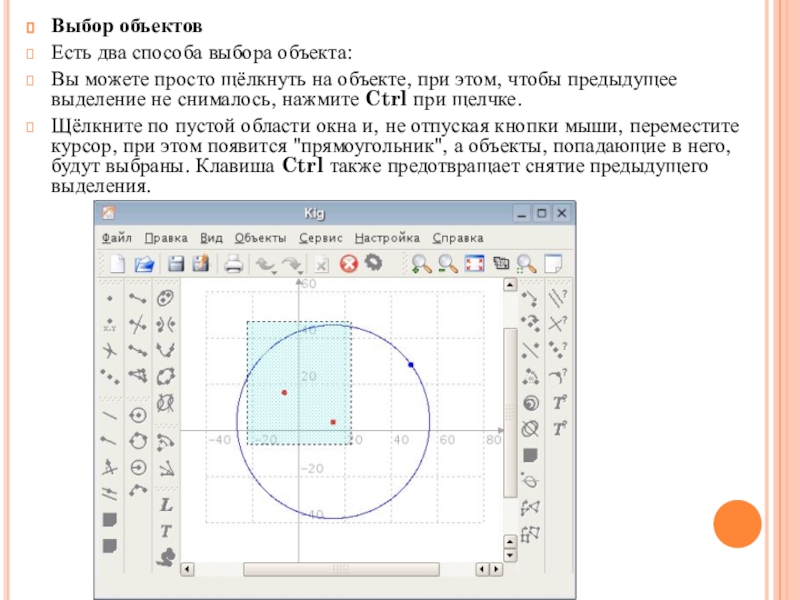
Слайд 34Выбор объектов
Есть два способа выбора объекта:
Вы можете просто щёлкнуть на
объекте, при этом, чтобы предыдущее выделение не снималось, нажмите Ctrl при щелчке.
Щёлкните
по пустой области окна и, не отпуская кнопки мыши, переместите курсор, при этом появится "прямоугольник", а объекты, попадающие в него, будут выбраны. Клавиша Ctrl также предотвращает снятие предыдущего выделения.Слайд 35Надписи
Для создания надписи нажмите соответствующую кнопку на панели инструментов, или
в меню Объекты → Другие → Надпись.
Затем вам нужно выбрать расположение новой надписи. Для этого
щёлкните на области экрана, где должна находится надпись или выберите в контекстном меню какого-либо объекта действие добавления к нему надписи.Слайд 36«Математический конструктор 1С»
«Математический конструктор» – незаменимый помощник автора учебных материалов,
в том числе учителя. В простейшем случае он позволяет легко
создавать качественные рисунки для вставки в печатные тексты.Слайд 37Возможности «Математического конструктора»:
Динамические геометрические построения
Измерения и вычисления
Функции и графики
Конические сечения
и другие кривые
Области и операции над ними
Автоматическая проверка построений и
тестовТекстовый редактор с вводом формул
Построение анимаций
Экспорт рисунков и апплетов
Настройка панелей инструментов в моделях
Интуитивно понятный интерфейс
Пользовательские инструменты и скрипты
Коллекция интерактивных обучающих моделей
Создание аккуратных чертежей и графиков
Самостоятельное исследование и эксперимент
Быстрые построения при работе на уроке
Организация проектной деятельности учащихся
Создание обучающих и контрольных материалов