Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рекурсия 9 класс
Содержание
- 1. Рекурсия 9 класс
- 2. Рекурсия — это такой способ организации вспомогательного
- 3. Уроборос – змей, пожирающий свой хвост. Рисунок
- 4. Program n1; uses crt;procedure Rec(i: integer);begin if
- 5. Вызов Rec(5)Вызов Rec(4)Вызов Rec(3)Вызов Rec(2)Вызов Rec(1)Вывод (1)Вывод
- 6. Процедура 5Процедура 4Процедура 3Процедура 2Процедура 1Вывод 5Вывод
- 7. Program n2;uses crt;procedure Rec(i: integer);begin writeln(i); if
- 8. i>1 Вывод i
- 9. Процедура 4Процедура 3Процедура 2Процедура 1Процедура 5Вывод 5Вывод
- 10. Program n3;Uses crt;Procedure Print(n:integer);Begin Writeln ('У
- 11. Program n4;uses crt;procedure Rec(i: integer);begin writeln(i); if
- 12. Задача. Заполнить массив из 5 элементов порядковыми
- 13. uses crt;var s,i:integer; a:array[1..5] of integer;procedure
- 14. Program n5_2;uses crt;Var a:array[1..5] of integer;
- 15. Последовательность, каждый член которой, начиная со второго,
- 16. Program n6;uses crt;Var k,I: integer;Function
- 17. Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн
- 18. uses crt;var fac: longint; n,
- 19. Факториал рекурсиейuses crt;var n:integer;function fac (
- 20. Задачи для самостоятельного решения1. Определим функцию K(n), которая
- 21. Математиком Исследовательского центра корпорации IBM Бенуа Мандельбротом
- 22. Фракталы
- 23. uses crt, graphabc;var x,y,x2,y2,i:integer;begin clrscr; x :=
- 24. Фракталы
- 25. Фракталы
- 26. XYx,y: real; Начало линииx2,y2: real; Конец
- 27. uses crt, graphabc;procedure scroll(x,y,A,Stwol: real;n: integer );var
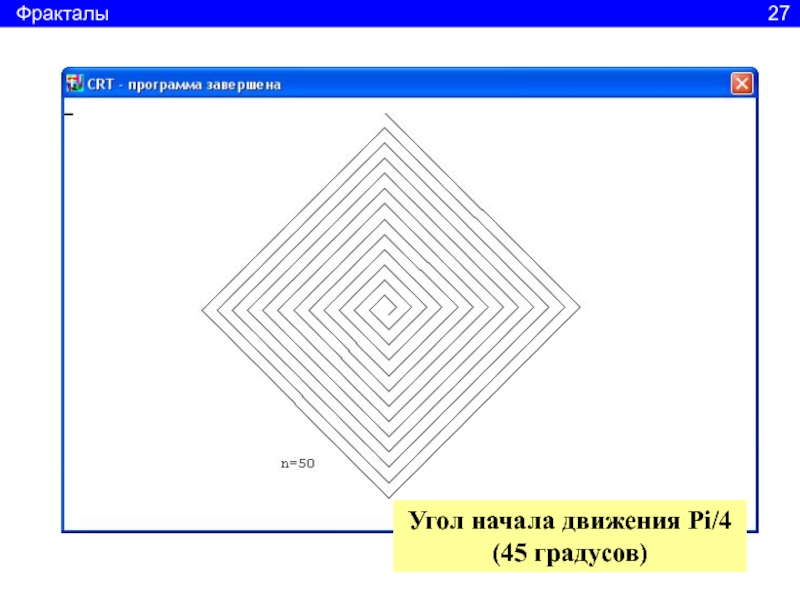
- 28. Угол начала движения Pi/4 (45 градусов)Фракталы
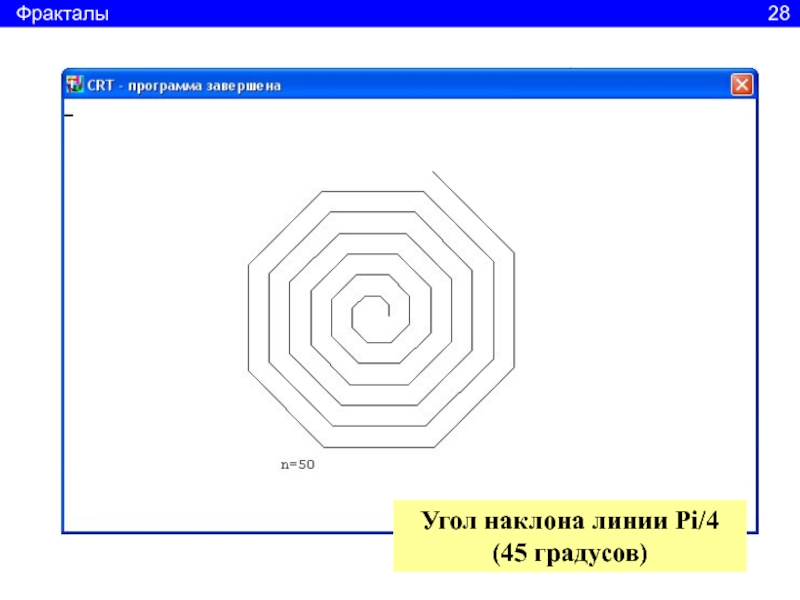
- 29. Угол наклона линии Pi/4 (45 градусов)Фракталы
- 30. Координаты корняКоординаты точки разветвленияУгол под которым растер
- 31. Stwol: real; длина ствола x2,y2: real; координаты
- 32. procedure Tree(x,y,A,Stwol: real;n: integer );var x2, y2:
- 33. begin clrscr; Tree(175, 325, Pi/2, 120, 14);
- 34. Треугольник Серпинского Фракталы
- 35. XYline(x,y,x2,y2)line(x3,y3,x2,y2)line(x,y,x3,y3)(x,y)(x2,y2)(x3,y3)(xa,ya)(xb,yb)(xc,yc)x,y xa, ya xc, ycx2,y2 xa, ya
- 36. procedure rec(x,y, x2,y2, x3,y3, n:integer); var xa,
- 37. Begin clrscr; rec(100,350,300,50,500,350,7);End.Вызываем рекурсивную процедуруФракталы
- 38. Задачи для самостоятельного решения1. Составьте программы выводящие
- 39. Задачи для самостоятельного решения2. Составьте программы выводящие
- 40. Задачи для самостоятельного решения3. Составьте программы выводящие
- 41. Задача. Необходимо составить программу для вычисления значений некоторого полинома (многочлена), определение которого имеет следующий вид: 40
- 42. function p(n:integer; x:real):real;{ n - степень полинома,
- 43. function p(n:integer; x:real):real;{ n - степень полинома,
- 44. uses crt,Utils ;var d1: DateTime;function p(n:integer; x:real):real;{определение
- 45. Рекурсивная функция:n = 35Время выполнения = 25,8 сИтеративная функция:n = 35Время выполнения
- 46. Light-bot - игра-головоломка для обучения программированию Описание функции F1Вызов функции F1 внутри функции F145
- 47. http://www.tvd-home.ru/recursion Персональная страничка Диканева Тараса Викторовичаhttp://comp-science.narod.ru/Progr/Rekursia.html Сайт
- 48. Златопольский Д.М. Программирование: типовые задачи, алгоритмы, методы.
- 49. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Рекурсия
Презентация к уроку информатики
Тема: программирование на языке PascalABC
Автор: Юдин
Андрей Борисович
Слайд 2Рекурсия — это такой способ организации вспомогательного алгоритма (подпрограммы), при
котором эта подпрограмма (процедура или функция) в ходе выполнения ее
операторов обращается сама к себе.Рекурсивным называется любой объект, который частично определяется через себя.
Определение рекурсии 1
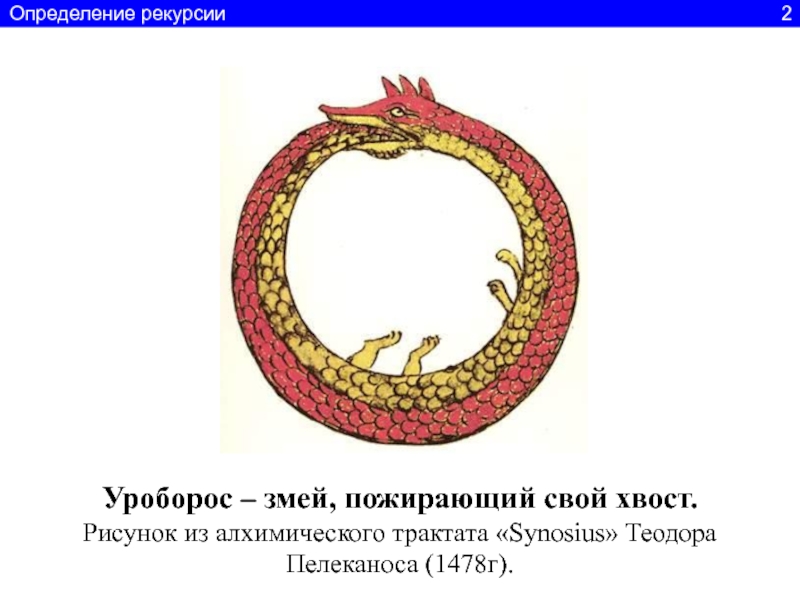
Слайд 3Уроборос – змей, пожирающий свой хвост.
Рисунок из алхимического трактата
«Synosius» Теодора Пелеканоса (1478г).
Определение рекурсии
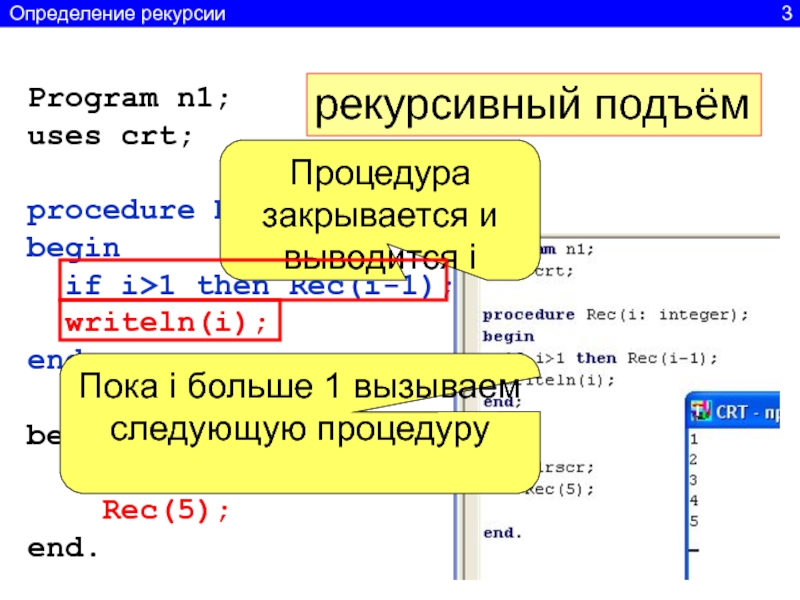
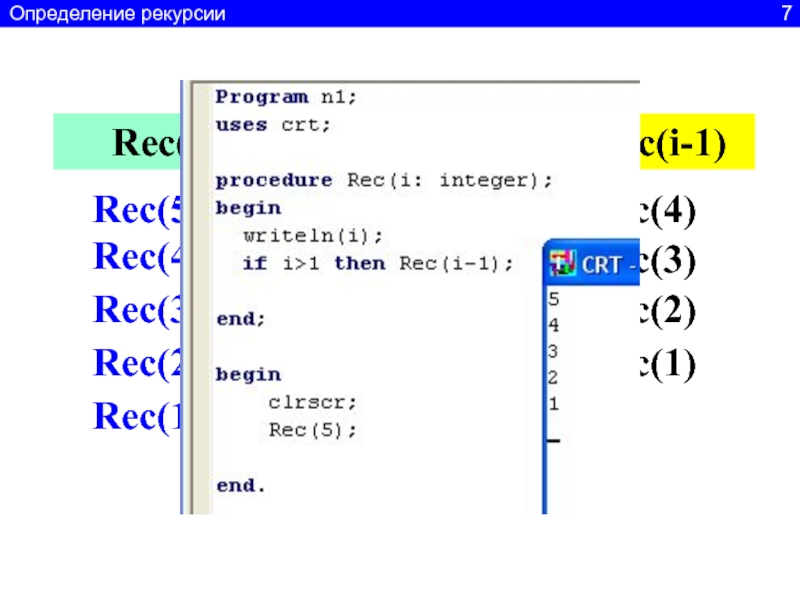
2Слайд 4Program n1;
uses crt;
procedure Rec(i: integer);
begin
if i>1 then Rec(i-1);
writeln(i);
end;
begin
clrscr;
Rec(5);
end.
рекурсивный подъём
Процедура закрывается и выводится i
Пока
i больше 1 вызываем следующую процедуру Определение рекурсии 3
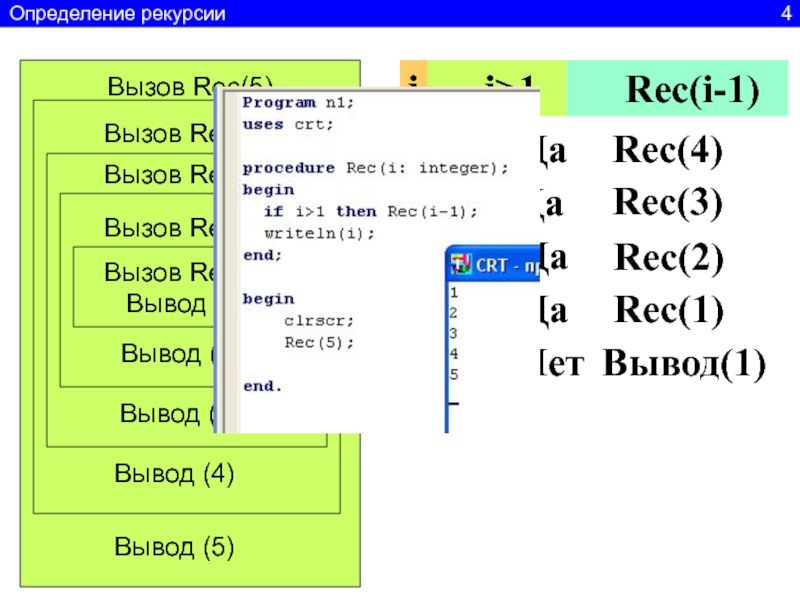
Слайд 5Вызов Rec(5)
Вызов Rec(4)
Вызов Rec(3)
Вызов Rec(2)
Вызов Rec(1)
Вывод (1)
Вывод (2)
Вывод (3)
Вывод (4)
Вывод
(5)
i>1
i
Rec(i-1)
5
4
3
2
1
5>1 Да
4>1 Да
3>1 Да
2>1 Да
1>1 Нет
Rec(4)
Rec(3)
Rec(2)
Rec(1)
Вывод(1)
Определение рекурсии 4
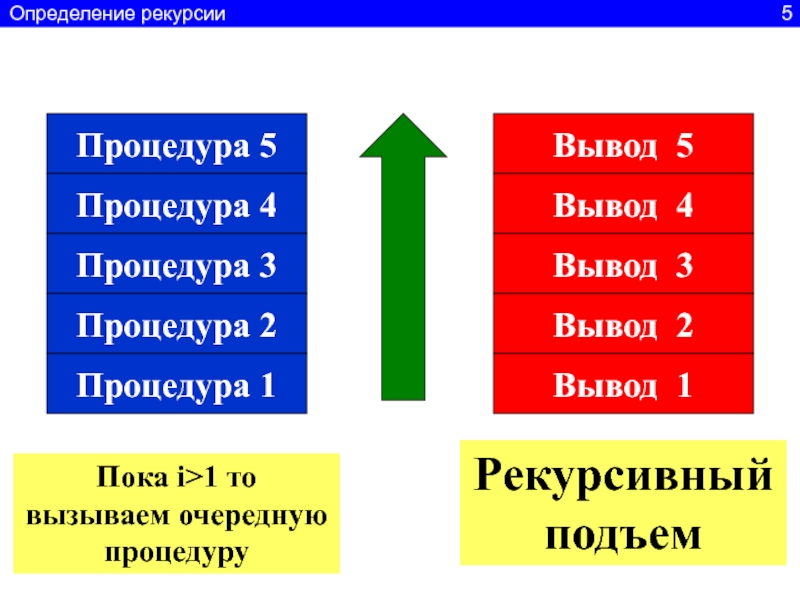
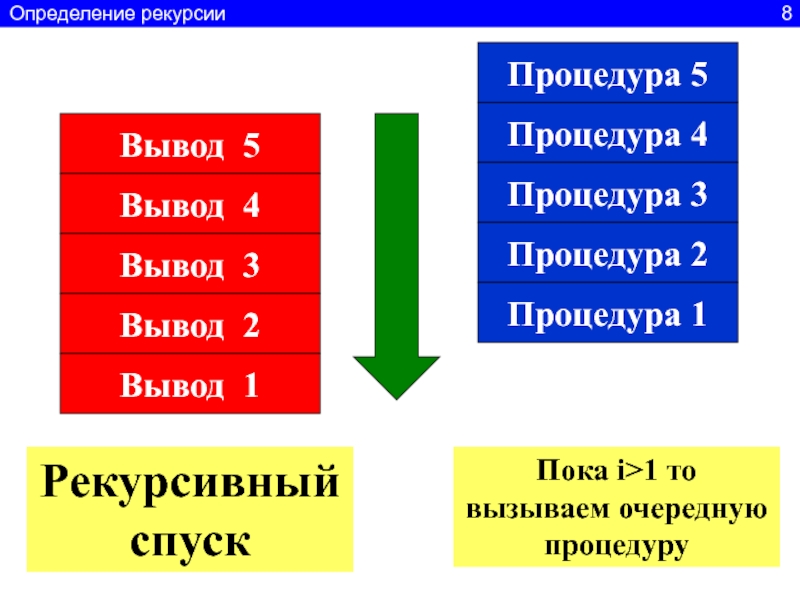
Слайд 6Процедура 5
Процедура 4
Процедура 3
Процедура 2
Процедура 1
Вывод 5
Вывод 4
Вывод 3
Вывод 2
Вывод
1
Пока i>1 то вызываем очередную
процедуру
Рекурсивный подъем
Определение рекурсии
5Слайд 7Program n2;
uses crt;
procedure Rec(i: integer);
begin
writeln(i);
if i>1 then Rec(i-1);
end;
begin
clrscr;
Rec(5);
end.
рекурсивный спуск
Вывод
Переход к следующей процедуре
Определение рекурсии
6Слайд 8 i>1
Вывод i
Rec(i-1)
5
4
3
2
1
5>1
Да
4>1 Да
3>1 Да
2>1 Да
1>1 Нет
Rec(4)
Rec(3)
Rec(2)
Rec(1)
Rec(i)
Rec(5)
Rec(4)
Rec(3)
Rec(2)
Rec(1)
Определение рекурсии 7
Слайд 9Процедура 4
Процедура 3
Процедура 2
Процедура 1
Процедура 5
Вывод 5
Вывод 4
Вывод 3
Вывод 2
Вывод
1
Пока i>1 то вызываем очередную
процедуру
Рекурсивный спуск
Определение рекурсии
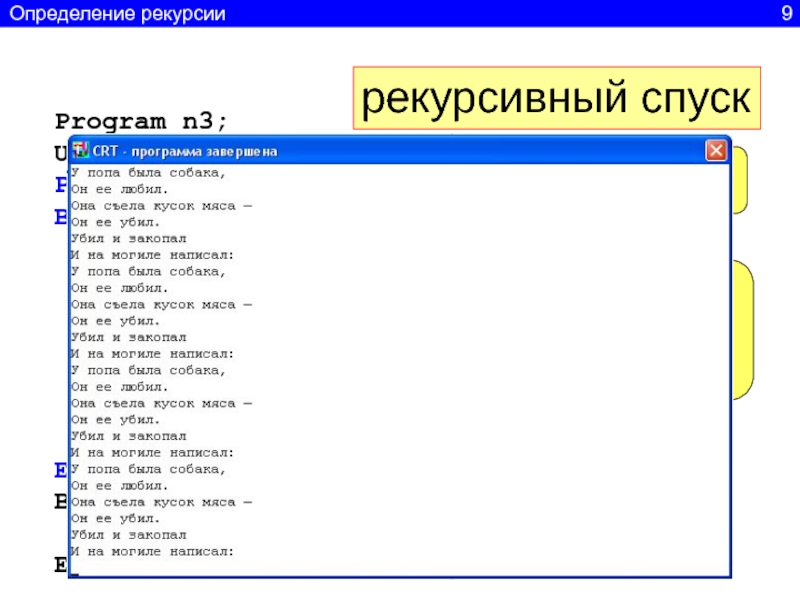
8Слайд 10Program n3;
Uses crt;
Procedure Print(n:integer);
Begin
Writeln ('У попа была собака,');
Writeln ('Он ее любил.');
Writeln ('Она съела кусок
мяса —');Writeln ('Он ее убил.');
Writeln ('Убил и закопал');
Writeln ('И на могиле написал:');
if n>1 then Print(n-1);
End;
BEGIN
Print(4);
END.
рекурсивный спуск
Вывод
Переход к следующей процедуре
Определение рекурсии 9
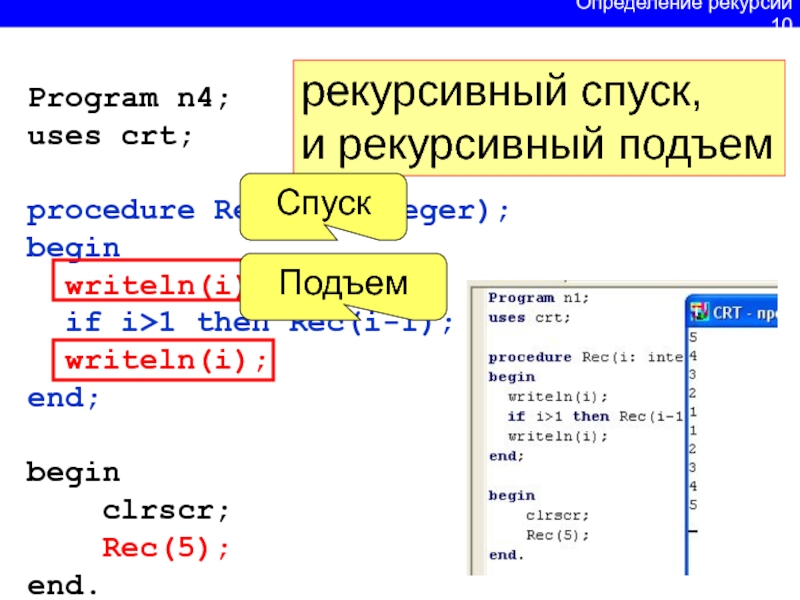
Слайд 11Program n4;
uses crt;
procedure Rec(i: integer);
begin
writeln(i);
if i>1 then Rec(i-1);
writeln(i);
end;
begin
clrscr;
Rec(5);
end.
рекурсивный спуск,
и рекурсивный подъем
Спуск
Подъем
Определение рекурсии 10
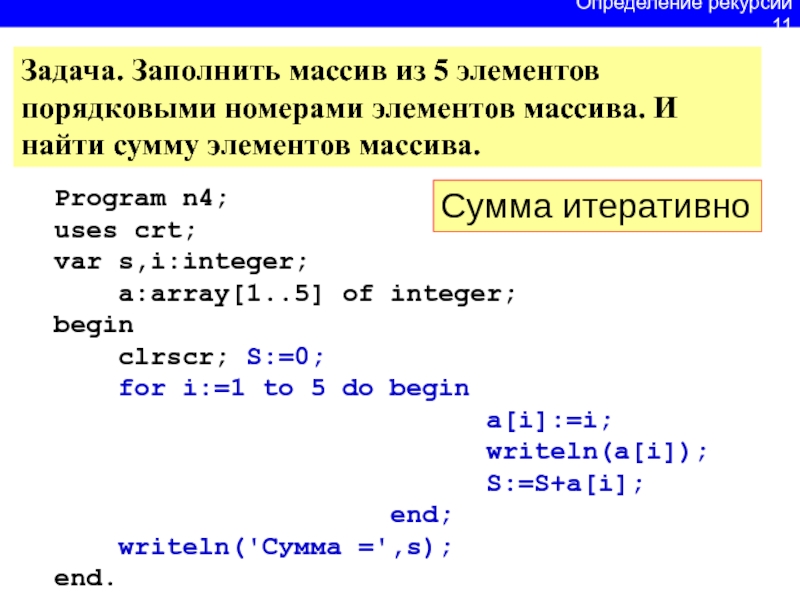
Слайд 12Задача. Заполнить массив из 5 элементов порядковыми номерами элементов массива.
И найти сумму элементов массива.
Program n4;
uses crt;
var s,i:integer;
a:array[1..5] of integer; begin
clrscr; S:=0;
for i:=1 to 5 do begin
a[i]:=i;
writeln(a[i]);
S:=S+a[i];
end;
writeln('Cумма =',s);
end.
Сумма итеративно
Определение рекурсии 11
Слайд 13uses crt;
var s,i:integer;
a:array[1..5] of integer;
procedure summ(i: integer);
begin
if
i>1 then summ(i-1);
begin
S:=S+a[i];
writeln(a[i]);
end;end;
begin
clrscr;
for i:=1 to 5 do a[i]:=i;
summ(5);
writeln('Сумма=',s);
end.
Рекурсивная процедура
Определение рекурсии 12
Процедура
Вызов процедуры из основной программы
Слайд 14Program n5_2;
uses crt;
Var a:array[1..5] of integer;
I:
integer;
Function Summ(i : integer) : Integer;
Begin
If i =
0 Then Summ := 0Else Summ := A[i] + Summ(i - 1)
End;
Begin
clrscr;
for i:=1 to 5 do a[i]:=i;
WriteLn('Cумма = ', Summ(5))
End.
Рекурсивная функция
Определение рекурсии 13
Функция
Вызов функции из основной программы
Слайд 15Последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному
с одним и тем же числом d, называется арифметической прогрессией. Число d -
разность прогрессии. Таким образом, арифметическая прогрессия есть последовательность, заданная рекуррентно равенством: Например:
Определение рекурсии 14
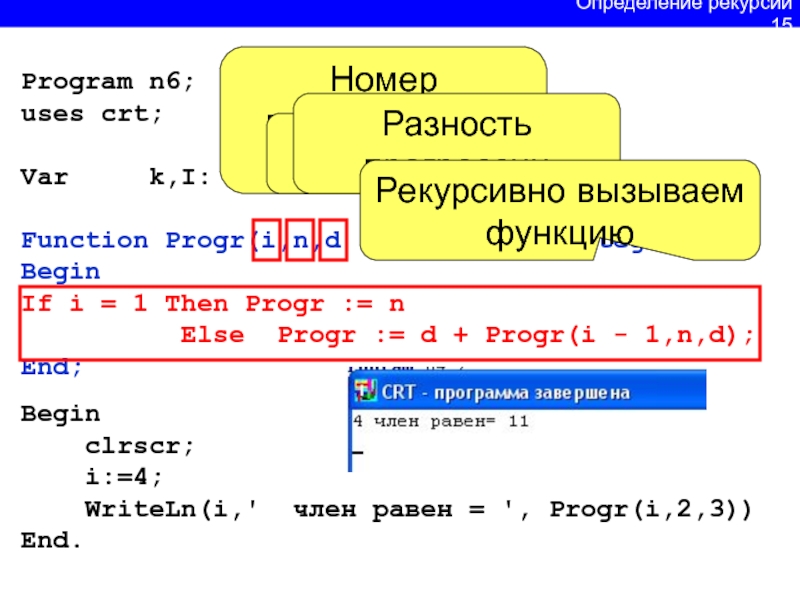
Слайд 16Program n6;
uses crt;
Var k,I: integer;
Function Progr(i,n,d : integer)
: Integer;
Begin
If i = 1 Then Progr := n
Else Progr := d + Progr(i - 1,n,d);End;
Begin
clrscr;
i:=4;
WriteLn(i,' член равен = ', Progr(i,2,3))
End.
Номер вычисляемого элемента
Первый элемент
Разность прогрессии
Определение рекурсии 15
Рекурсивно вызываем функцию
Слайд 17Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел
от 1 до n включительно.
если n=0 или n=1
если n>1
Например:
5!=1∙2∙3∙4∙5=120
Например:
1!=1
2!=1! ∙ 2=1 ∙
2=23!=2! ∙3=2 ∙ 3=6
4!=3! ∙4=6 ∙ 4=24
5!=4! ∙5=24 ∙5=120
Определение рекурсии 16
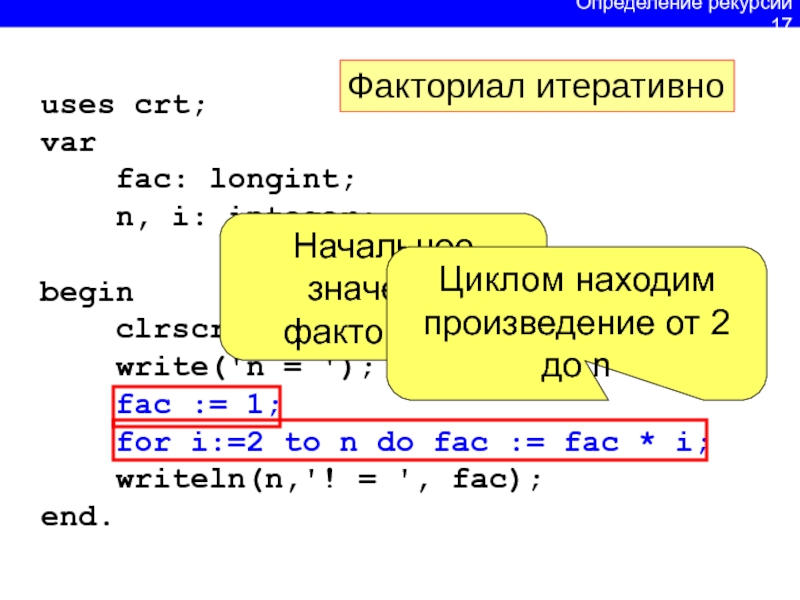
Слайд 18uses crt;
var
fac: longint;
n, i: integer;
begin
clrscr;
write('n = '); readln(n);
fac := 1;
for i:=2 to n do fac := fac * i;writeln(n,'! = ', fac);
end.
Начальное значение факториала
Циклом находим произведение от 2 до n
Определение рекурсии 17
Факториал итеративно
Слайд 19Факториал рекурсией
uses crt;
var n:integer;
function fac ( n : integer):
integer;
begin
if (n = 1) or (n=0) then fac := 1
else fac:= n*fac(n-1);end;
begin
clrscr;
write('n = '); readln(n);
writeln(n,'! = ', fac(n));
end.
Начальное значение факториала
Вызываем повторно функцию вычисления факториала
Определение рекурсии 18
Слайд 20Задачи для самостоятельного решения
1. Определим функцию K(n), которая возвращает количество цифр
в заданном натуральном числе n. Составить программу определяющую количество цифр
в числе с использованием рекурсии.2. Разработать программу для нахождения наибольшего общего делителя (НОД) двух заданных натуральных чисел используя алгоритм Евклида
Определение рекурсии 19
Слайд 21Математиком Исследовательского центра корпорации IBM Бенуа Мандельбротом в 1975 году
был введен термин “фрактал” (от латинского fractus – раздробленный, разбитый,
состоящий из фрагментов), а в 1982 году опубликована основополагающая книга “Фрактальная геометрия природы”, где описаны фрактальные множества, их свойства, методы получения и изображения.Фракталы 20
Слайд 22Фракталы
21
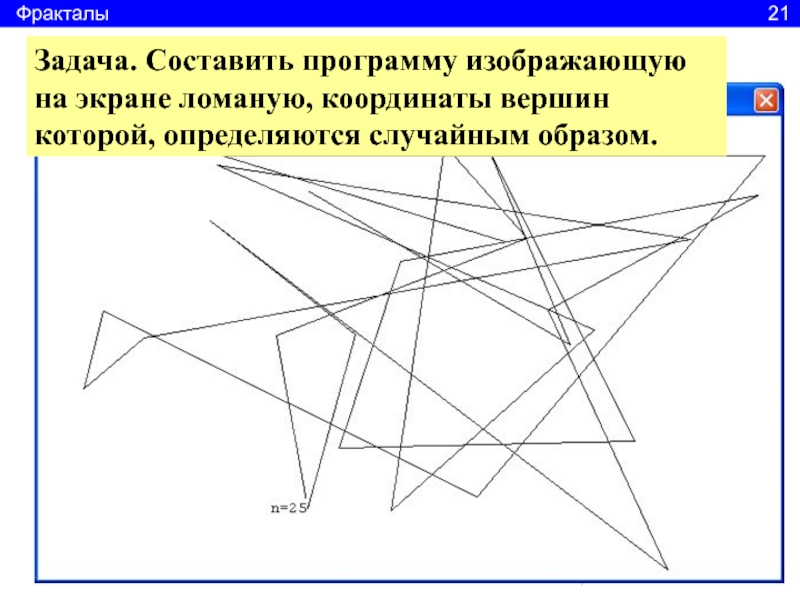
Задача. Составить программу изображающую на экране ломаную, координаты вершин которой, определяются случайным образом.
Слайд 23uses crt, graphabc;
var x,y,x2,y2,i:integer;
begin
clrscr;
x := random(640);
y :=
random(400);
for i:=1 to 25 do begin
x2 := random(640);y2 := random(400);
line(x,y,x2,y2);
x:=x2;
y:=y2;
end;
textout(200,330,'n=25');
end.
Координаты начала первой линии
Цикл задающий количество звеньев
Координаты конца линии
Линия
Координаты конца линии становятся координатами начала следующей линии
Фракталы 22
Слайд 24Фракталы
23
uses crt, graphabc;
procedure segment(x,y,x2,y2,n: integer );
begin
x2 := random(640);
y2 := random(400);
line(x,y,x2,y2);
if n > 1 then
segment(x2,y2,random(640),random(400),n-1);
end;
begin
clrscr;
segment(320,200, 0, 0, 25);
textout(200,330,'n=25');
end.
Координаты начала линии
Линия
Пока n>1 вызываем еще одну процедуру
Координаты начала звена
Координаты конца звена
Количество звеньев
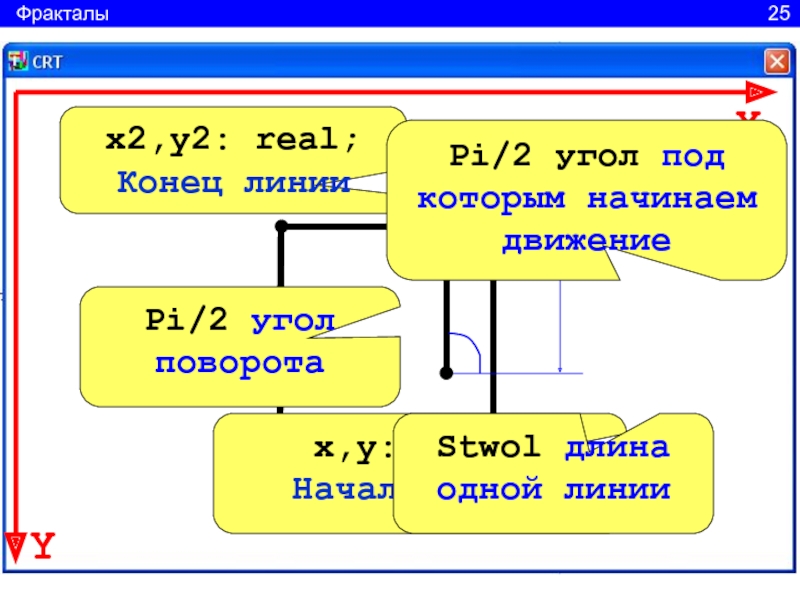
Слайд 26
X
Y
x,y: real;
Начало линии
x2,y2: real;
Конец линии
Pi/2 угол поворота
Pi/2
угол под которым начинаем движение
Stwol длина одной линии
Фракталы
25Слайд 27uses crt, graphabc;
procedure scroll(x,y,A,Stwol: real;n: integer );
var
x2, y2: real;
begin
x2 := x + Stwol * cos(A);
y2 := y - Stwol * sin(A);line(round(x), round(y), round(x2), round(y2));
if n > 1 then
scroll( x2, y2, A+Pi/2, Stwol+5, n-1);
end;
begin
clrscr;
scroll(300, 200, Pi/2, 10, 50);
textout(200,330,'n=50');
end.
Вычисляем координаты конца линии
Рисуем линию
Пока n>1 вызываем процедуру рисования линии
Для каждой следующей линии поворачиваем на 90 градусов
Каждую новую линию удлиняем на 5 единиц
Фракталы 26
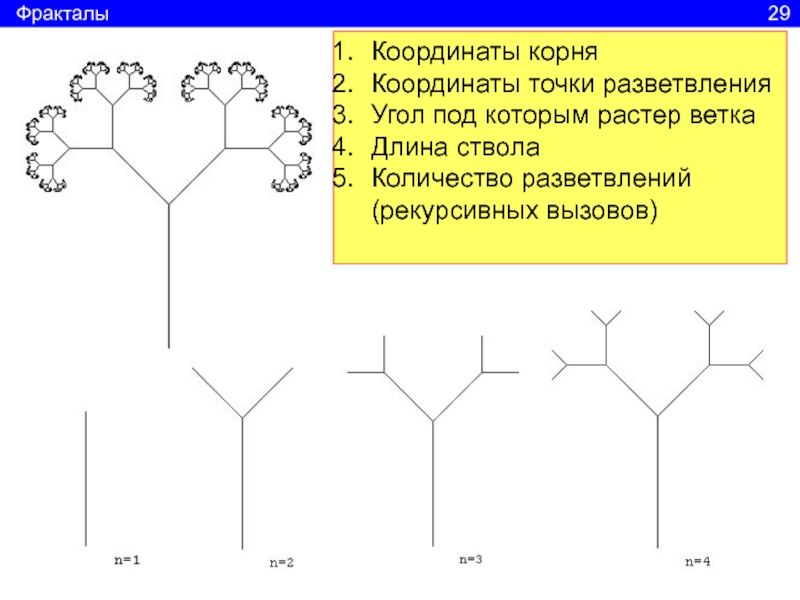
Слайд 30Координаты корня
Координаты точки разветвления
Угол под которым растер ветка
Длина ствола
Количество разветвлений
(рекурсивных вызовов)
Фракталы
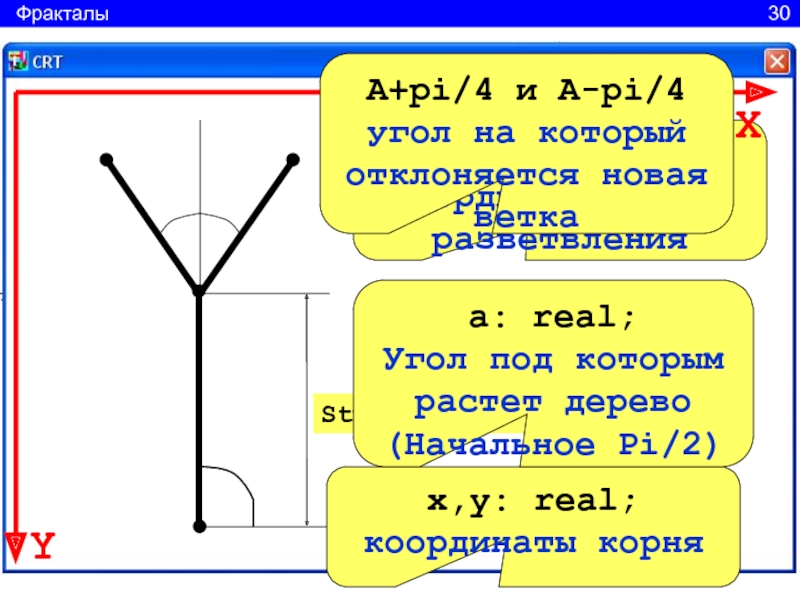
29Слайд 31Stwol: real; длина ствола
x2,y2: real; координаты точки разветвления
x,y: real;
координаты корня
а: real;
Угол под которым растет дерево
(Начальное Pi/2)
X
Y
A+pi/4 и
A-pi/4 угол на который отклоняется новая веткаФракталы 30
Слайд 32procedure Tree(x,y,A,Stwol: real;n: integer );
var
x2, y2: real;
begin
x2 := x + Stwol * cos(A);
y2 :=
y - Stwol * sin(A);line(round(x), round(y),round(x2), round(y2));
if n > 1 then
begin
Tree( x2, y2, A+Pi/4, 0.6*Stwol, n-1);
Tree( x2, y2, A-Pi/4, 0.6*Stwol, n-1);
end;
end;
Координаты точки разветвления
Рисуем одну ветвь
Пока n>1 два раза вызываем процедуру для правой и левой ветки
Фракталы 31
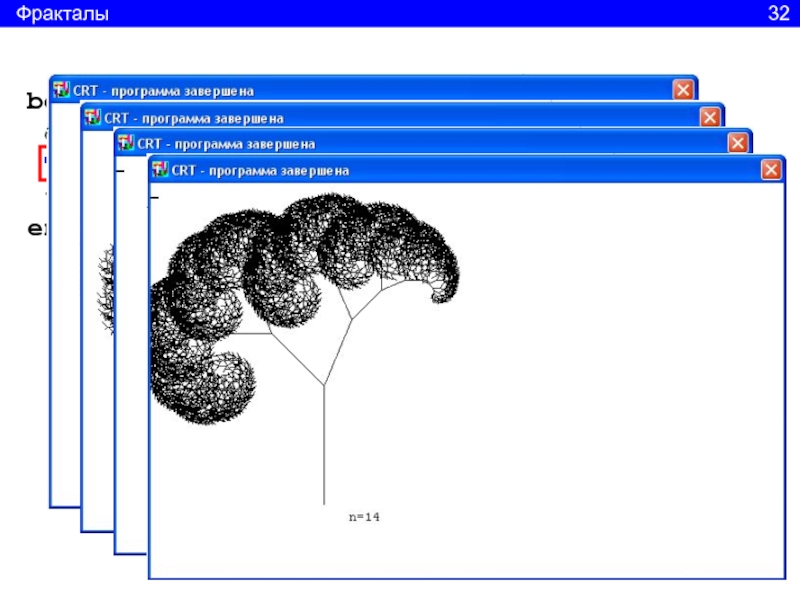
Слайд 33begin
clrscr;
Tree(175, 325, Pi/2, 120, 14);
textout(200,330,'n=14');
end.
Вызов рекурсивной процедуры
из тела программы
Фракталы
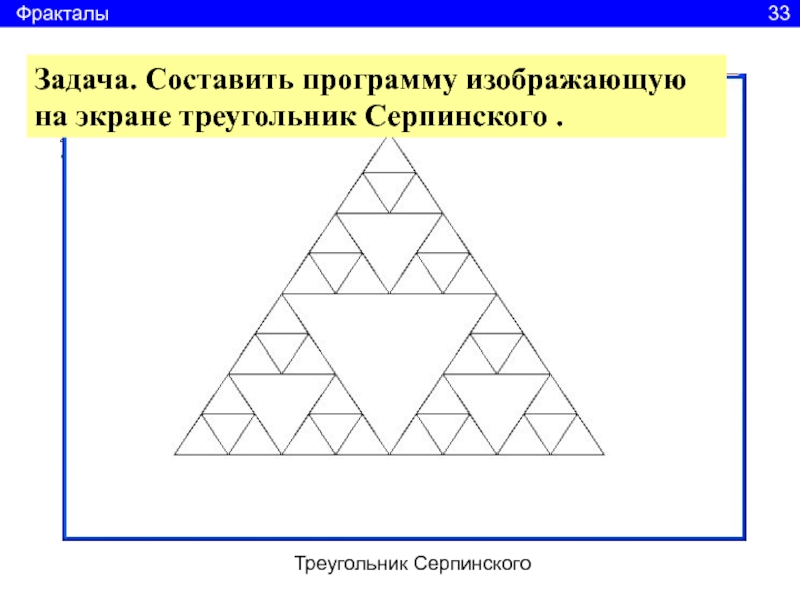
32Слайд 34Треугольник Серпинского
Фракталы
33
Задача. Составить программу изображающую на экране треугольник Серпинского .
Слайд 35X
Y
line(x,y,x2,y2)
line(x3,y3,x2,y2)
line(x,y,x3,y3)
(x,y)
(x2,y2)
(x3,y3)
(xa,ya)
(xb,yb)
(xc,yc)
x,y
xa, ya
xc, yc
x2,y2
xa, ya
xb, yb
x3,y3
xb,
yb
xc, yc
Фракталы
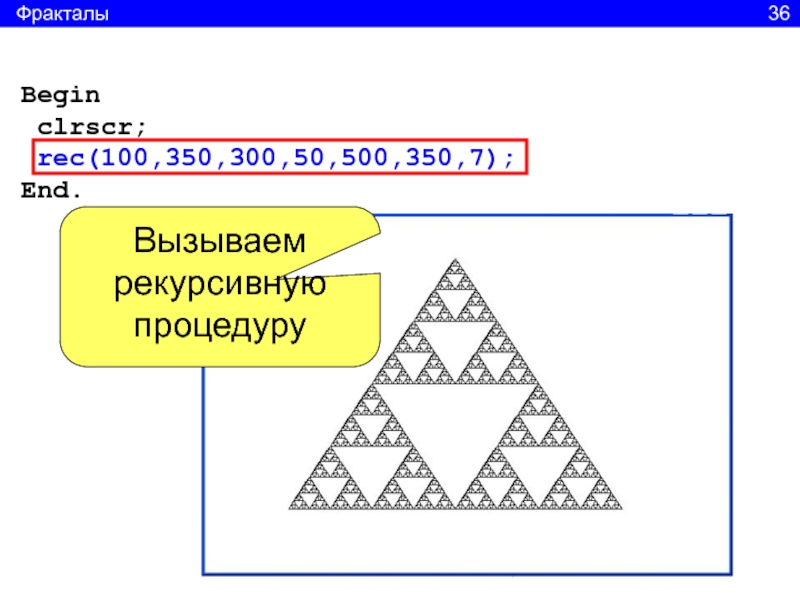
34Слайд 36procedure rec(x,y, x2,y2, x3,y3, n:integer);
var xa, ya, xb, yb,
xc, yc:integer;
begin
if n >0 then
begin
line(x,y,x2,y2);line(x3,y3,x2,y2);
line(x,y,x3,y3);
xa:=(x+x2) div 2; ya:=(y+y2) div 2;
xb:=(x3+x2) div 2; yb:=(y3+y2) div 2;
xc:=(x+x3) div 2; yc:=(y+y3) div 2;
rec(x,y,xa, ya, xc, yc, n-1);
rec(x2,y2,xa, ya, xb, yb, n-1);
rec(x3,y3,xb, yb, xc, yc, n-1);
end;
end;
Рисуем треугольник
Вычисляем координаты середин сторон треугольника
Рекурсивно рисуем три меньших треугольника
Фракталы 35
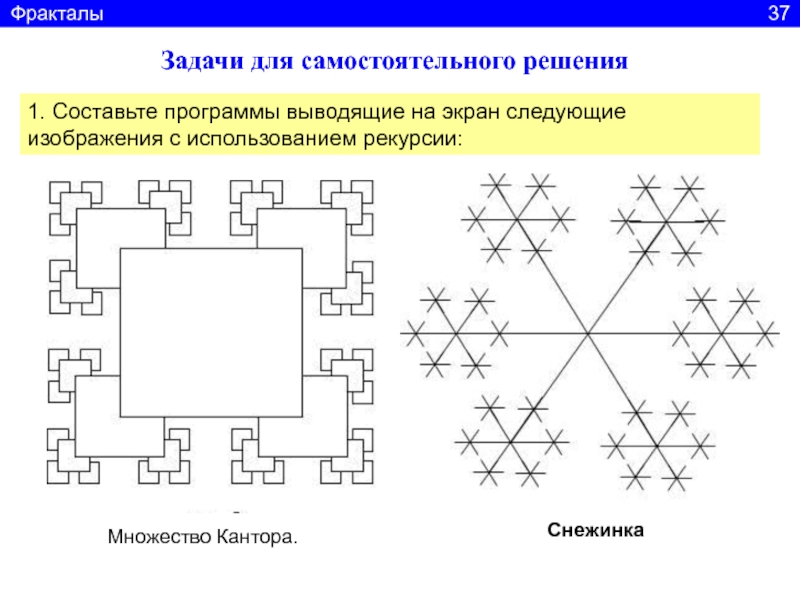
Слайд 38Задачи для самостоятельного решения
1. Составьте программы выводящие на экран следующие
изображения с использованием рекурсии:
Фракталы
37Множество Кантора.
Снежинка
Слайд 39Задачи для самостоятельного решения
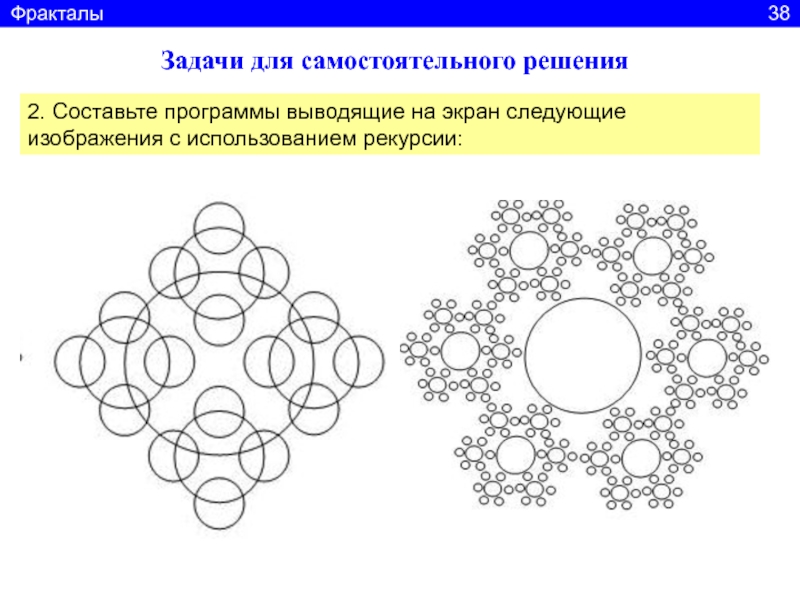
2. Составьте программы выводящие на экран следующие
изображения с использованием рекурсии:
Фракталы
38Слайд 40Задачи для самостоятельного решения
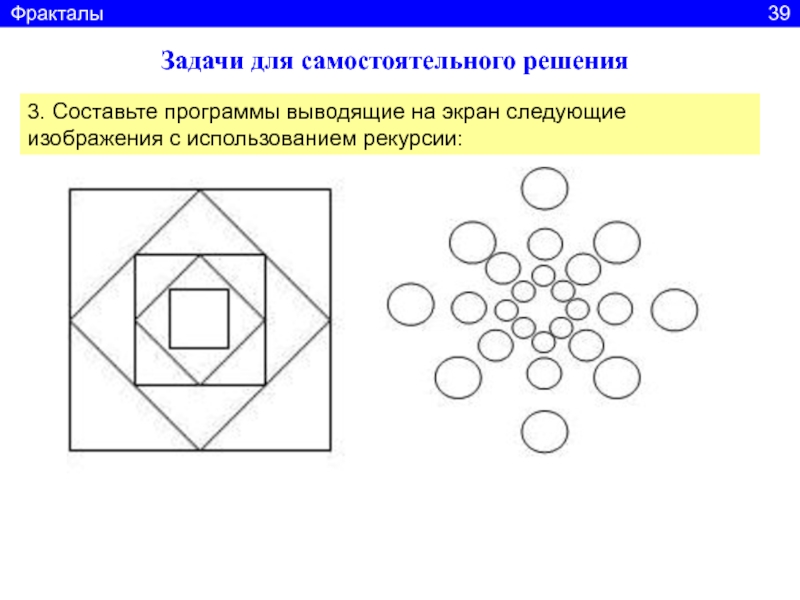
3. Составьте программы выводящие на экран следующие
изображения с использованием рекурсии:
Фракталы
39Слайд 41
Задача. Необходимо составить программу для вычисления значений некоторого полинома (многочлена),
определение которого имеет следующий вид:
40
Слайд 42function p(n:integer; x:real):real;
{ n - степень полинома, x- значение аргумента}
var
p0,p1,p2:real; i:integer;
begin
if n=0 then p:=0
else if n=1 then p:=2*x
else beginp0:=0;
p1:=2*x;
for i:=2 to n do begin
p2:=2*i/(i-1)*p1+(i-1)/(2*i)*p0;
p0:=p1;
p1:=p2;
end;
p:=p2;
end;
end;
Значения полинома при 0 и 1
Устанавливаем начальные значения
Вычисляем значения полинома до n используя цикл
Итеративная функция:
41
Слайд 43function p(n:integer; x:real):real;
{ n - степень полинома, x- значение аргумента}
begin
if
n=0 then
p:=0
else if n=1 then p:=2*x
else
p:=2*n/(n-1)*p(n-1,x)+(n-1)/(2*n)*p(n-2,x);
end;
Значения полинома при 0 и 1
Вызываем функцию повторно
Рекурсивная функция:
42
Слайд 44uses crt,Utils ;
var d1: DateTime;
function p(n:integer; x:real):real;
{определение функции}
begin
clrscr;
d1 := CurrentDateTime;
Writeln(' Время: ',d1.hour,':',d1.minute,
':',d1.second,':',d1.Milliseconds div 100);writeln(p(35,5));
d1 := CurrentDateTime;
Writeln(' Время: ',d1.hour,':',d1.minute,
':',d1.second,':',d1.Milliseconds div 100);
end.
Здесь поместим одну из описанных выше функций
Переменная для хранения системного времени
Считываем системное время и выводим его на экран
Вызываем функцию
Считываем системное время и выводим его на экран
43
Слайд 45Рекурсивная функция:
n = 35
Время выполнения =
25,8 с
Итеративная функция:
n =
35
Время выполнения
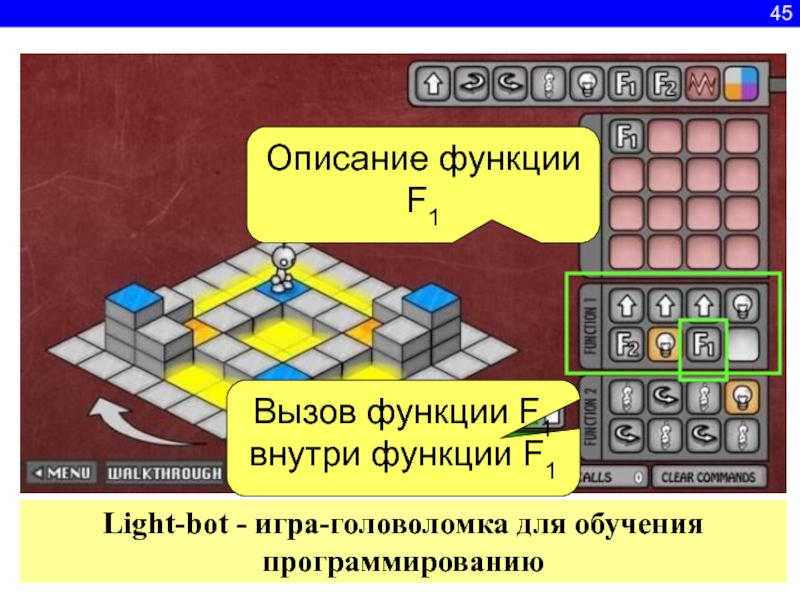
Слайд 46Light-bot - игра-головоломка для обучения программированию
Описание функции F1
Вызов функции
F1 внутри функции F1
45
Слайд 47http://www.tvd-home.ru/recursion Персональная страничка
Диканева Тараса Викторовича
http://comp-science.narod.ru/Progr/Rekursia.html Сайт Шестакова Александра Петровича
http://fraktalsworld.blogspot.ru/
Сайт «В мире фракталов» автор Александр Чернышев
http://www.cyberforum.ru/pascalabc/thread994987.html Ветвь форума по
программированию. Автор ildwine. Интернет ресурсы:
46
Слайд 48Златопольский Д.М. Программирование: типовые задачи, алгоритмы, методы. М.: БИНОМ. Лаборатория
знаний, 2007
Бердж В. Методы рекурсивного программирования. Издательство: Машиностроение. 1983
Источник
для скачивания книги: http://progbook.ru/technologiya-programmirovaniya/924-berdj-metody-rekursivnogo-programmirovaniya.htmlГоловешкин В.А., Ульянов М. В. Теория рекурсии для программистов. М.: ФИЗМАТЛИТ, 2006.
Список литературы:
47



![Рекурсия 9 класс uses crt;var s,i:integer; a:array[1..5] of integer;procedure summ(i: integer);begin if i>1 then uses crt;var s,i:integer; a:array[1..5] of integer;procedure summ(i: integer);begin if i>1 then summ(i-1); begin S:=S+a[i];](/img/thumbs/3b57837b3d9fc5adab59f4083c3c670a-800x.jpg)
![Рекурсия 9 класс Program n5_2;uses crt;Var a:array[1..5] of integer; I: integer;Function Summ(i : Program n5_2;uses crt;Var a:array[1..5] of integer; I: integer;Function Summ(i : integer) : Integer;Begin](/img/thumbs/9f8a594060a8a134a78fea3bfb917e88-800x.jpg)