Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач линейного программирования в MS Excel
Содержание
- 1. Решение задач линейного программирования в MS Excel
- 2. Общая задача линейного программирования решается симплексным методомСимплекс
- 3. Если задача линейного программирования имеет оптимальное решение,
- 4. Геометрический смысл симплексного метода состоит в последовательном
- 5. Впервые симплексный метод был предложен американским ученым
- 6. Симплексный метод позволяет решить любую задачу линейного
- 7. В MS Excel для решения задачи линейного программирования используется надстройка ПОИСК РЕШЕНИЯ
- 8. Сначала надстройку Поиск решения необходимо подключить (до
- 9. В MS Excel 2007: 1) Кнопка
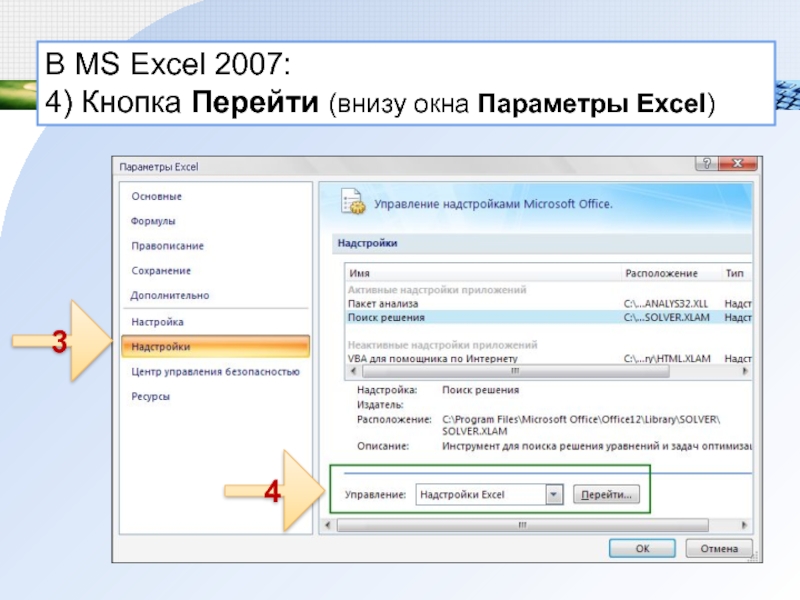
- 10. В MS Excel 2007: 4) Кнопка Перейти (внизу окна Параметры Excel) 43
- 11. В окне Надстройки установить флажок и нажать
- 12. В MS Excel 2007 кнопка Поиск решения появится во вкладке Данные
- 13. Решим в MS Excel задачу линейного программирования12
- 14. Решим в MS Excel задачу линейного программирования34СРССРС
- 15. Ответы:1234
- 16. Решим в MS Excel задачу линейного программирования1.
- 17. Решим в MS Excel задачу линейного программирования2.
- 18. Решим в MS Excel задачу линейного программирования3.
- 19. Решим в MS Excel задачу линейного программирования3.
- 20. Решим в MS Excel задачу линейного программирования3.
- 21. Решим в MS Excel задачу линейного программирования3.
- 22. Решим в MS Excel задачу линейного программирования4.
- 23. Решим в MS Excel задачу линейного программированияУстанавливаем
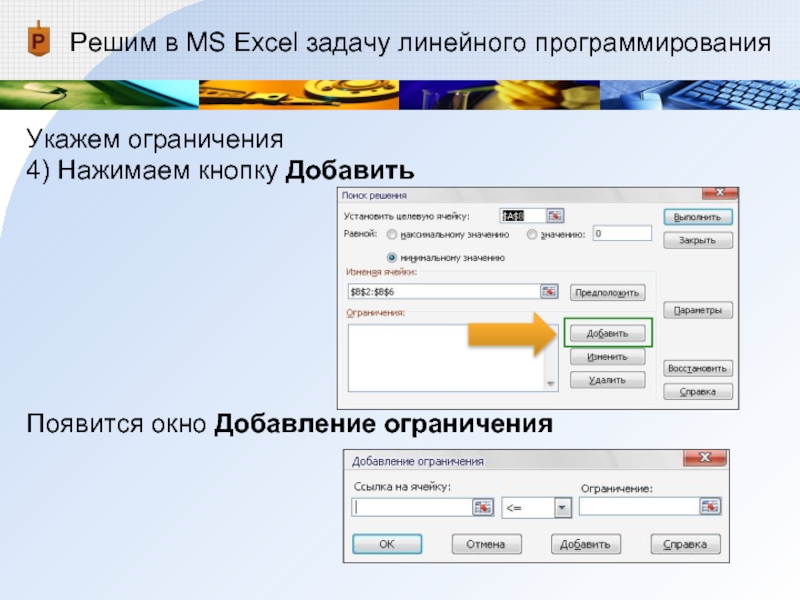
- 24. Решим в MS Excel задачу линейного программированияУкажем ограничения4) Нажимаем кнопку Добавить Появится окно Добавление ограничения
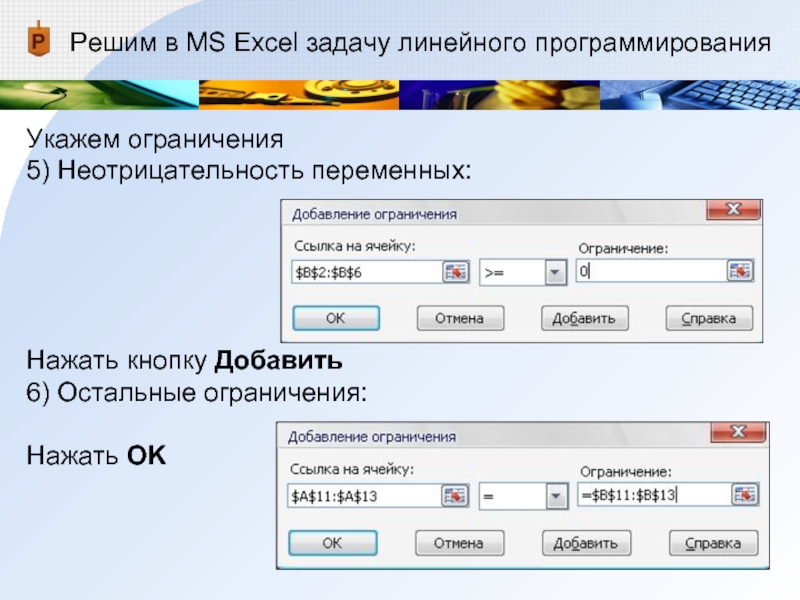
- 25. Решим в MS Excel задачу линейного программированияУкажем ограничения5) Неотрицательность переменных: Нажать кнопку Добавить6) Остальные ограничения:Нажать OK
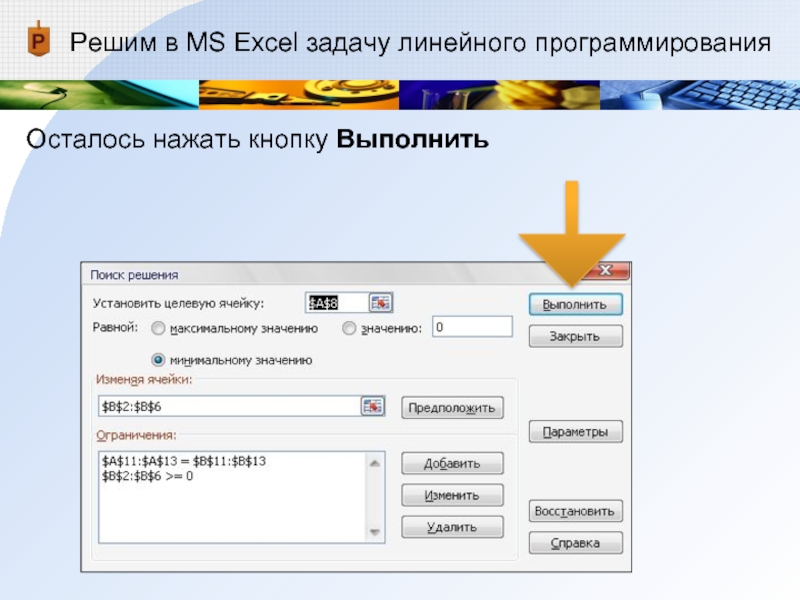
- 26. Решим в MS Excel задачу линейного программированияОсталось нажать кнопку Выполнить
- 27. Решим в MS Excel задачу линейного программированияРезультатыОтвет:
- 28. ЛитератураКремер Н.Ш., Путко Б.А. Исследование операций в
- 29. Скачать презентанцию
Общая задача линейного программирования решается симплексным методомСимплекс (лат. simplex - простой) – простейший выпуклый многогранник в n-мерном пространстве с n+1 вершиной (например, тетраэдр в 3-мерном пространстве)
Слайды и текст этой презентации
Слайд 2Общая задача линейного программирования решается симплексным методом
Симплекс (лат. simplex - простой)
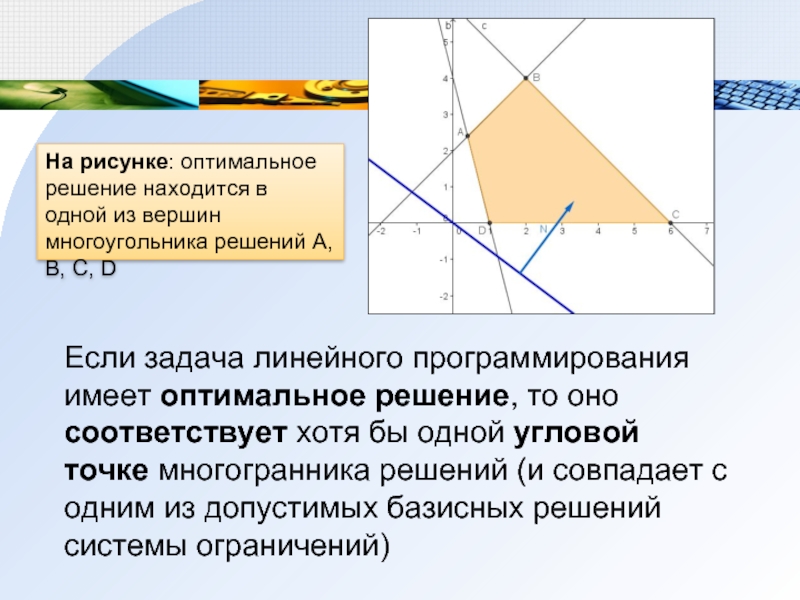
Слайд 3Если задача линейного программирования имеет оптимальное решение, то оно соответствует
хотя бы одной угловой точке многогранника решений (и совпадает с
одним из допустимых базисных решений системы ограничений)На рисунке: оптимальное решение находится в одной из вершин многоугольника решений А, В, С, D
Слайд 4Геометрический смысл симплексного метода состоит в последовательном переходе от одной
вершины многогранника ограничений к соседней, в которой целевая функция принимает
лучшее (по крайней мере, не худшее) значение
Слайд 5Впервые симплексный метод был предложен американским ученым Дж. Данцигом в
1949 г.
Джордж Бернард Данциг (1914-2005) – американский математик, разработал симплексный
алгоритм, считается основоположником методов линейного программированияЛеонид Витальевич Канторович (1912-1986) – советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов». Один из создателей линейного программирования
Идеи симплексного метода были разработаны в 1939 г. российским ученым Л.В.Канторовичем
Слайд 6Симплексный метод позволяет решить любую задачу линейного программирования
В настоящее время
он используется для компьютерных расчетов
Рассмотрим решение задачи линейного программирования в
MS Excel 
Слайд 7В MS Excel для решения задачи линейного программирования используется надстройка
ПОИСК РЕШЕНИЯ
Слайд 8Сначала надстройку Поиск решения необходимо подключить (до первого использования)
В MS
Excel 2003:
Сервис /
Надстройки /
Поиск решения /
OK
После
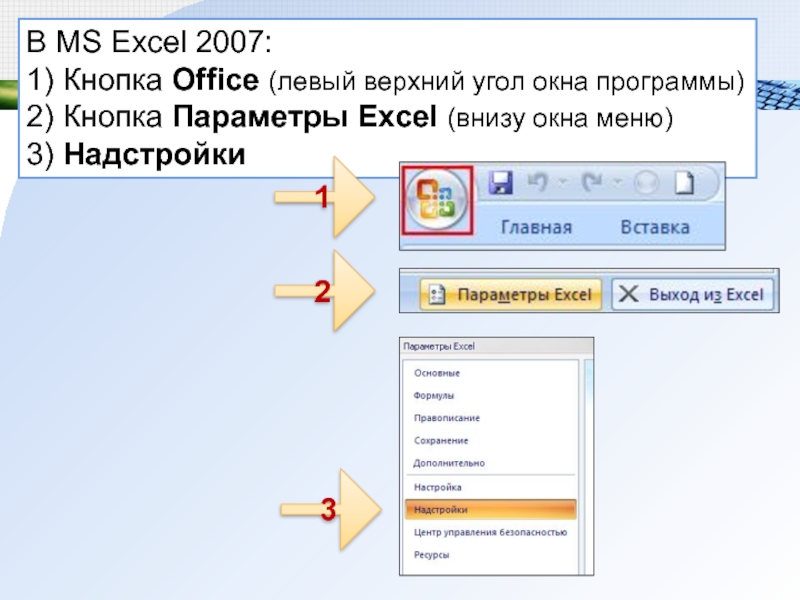
этого команда Поиск решения включена в меню Сервис
Слайд 9В MS Excel 2007: 1) Кнопка Office (левый верхний угол
окна программы)
2) Кнопка Параметры Excel (внизу окна меню)
3) Надстройки
1
2
3
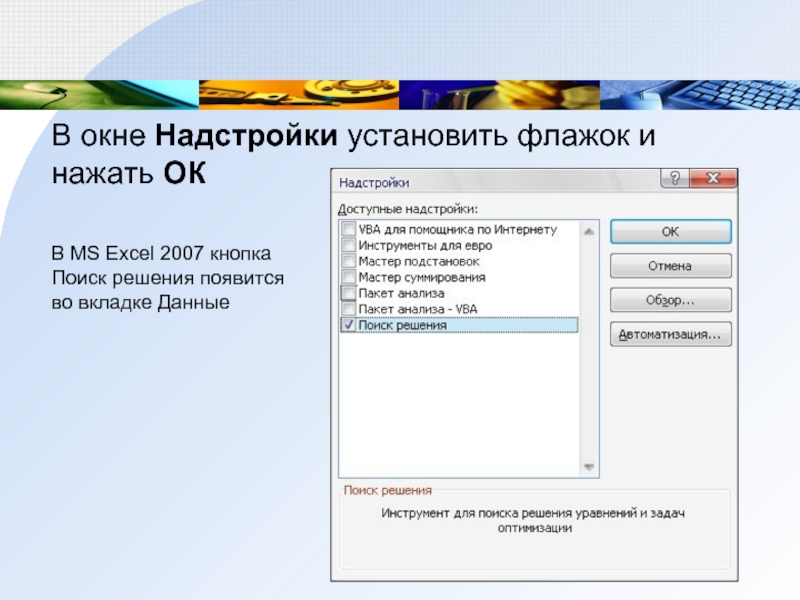
Слайд 11В окне Надстройки установить флажок и нажать ОК
В MS Excel
2007 кнопка Поиск решения появится во вкладке Данные
Слайд 16Решим в MS Excel задачу линейного программирования
1. Создадим область переменных
Ячейки
В2:В6 будут играть роль переменных
(пока они пусты)
Слайд 17Решим в MS Excel задачу линейного программирования
2. Введем формулу вычисления
значений целевой функции
Например, в ячейку А8
Слайд 18Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В
ячейках А11:А13 будем вычислять левые части ограничений в системе
В ячейках
В11:В13 введем правые части ограничений системы
Слайд 19Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В
ячейках А11:А13 будем вычислять левые части ограничений в системе
Первое ограничение
Слайд 20Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В
ячейках А11:А13 будем вычислять левые части ограничений в системе
Второе ограничение
Слайд 21Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В
ячейках А11:А13 будем вычислять левые части ограничений в системе
Третье ограничение
Слайд 22Решим в MS Excel задачу линейного программирования
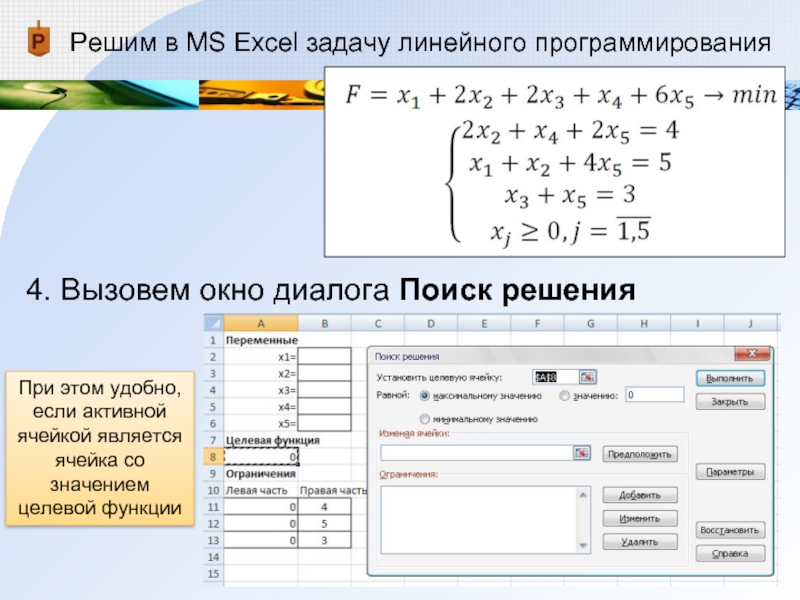
4. Вызовем окно диалога
Поиск решения
При этом удобно, если активной ячейкой является ячейка со
значением целевой функции
Слайд 23Решим в MS Excel задачу линейного программирования
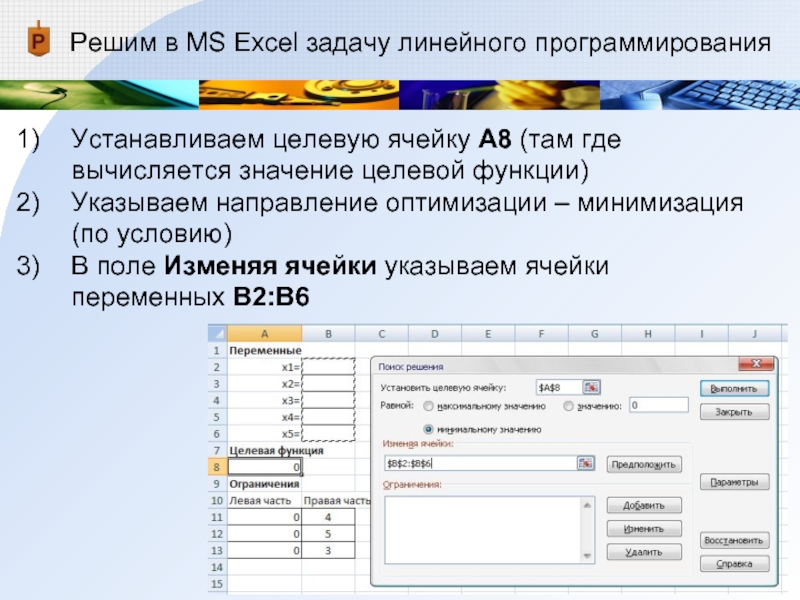
Устанавливаем целевую ячейку А8
(там где вычисляется значение целевой функции)
Указываем направление оптимизации – минимизация
(по условию)В поле Изменяя ячейки указываем ячейки переменных В2:В6
Слайд 24Решим в MS Excel задачу линейного программирования
Укажем ограничения
4) Нажимаем кнопку
Добавить
Появится окно Добавление ограничения
Слайд 25Решим в MS Excel задачу линейного программирования
Укажем ограничения
5) Неотрицательность переменных:
Нажать кнопку Добавить
6) Остальные ограничения:
Нажать OK
Слайд 28Литература
Кремер Н.Ш., Путко Б.А. Исследование операций в экономике. - М.:
ЮНИТИ, 2003. - 407 с.
Красс М.С., Чупрынов Б.П. Математика для
экономистов. - СПб.: Питер, 2005. - 464 с.
Теги
